Нахождение сильных компонент, базового и доминирующего множеств

При определении сильных компонент и базового множества ориентированного графа G используется матрица достижимости L и контрдостижимости Q графа [6]. Элементы l_ik и q_ik этих матриц определяются следующим образом:

=

=

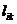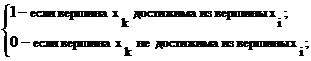
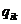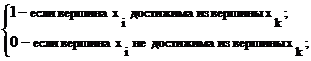
Матрица достижимости L графа G, имеющего n вершин, может быть получена путем последовательногобулевого умножения матрицы R¹ графа (достижимости не более чем за один шаг) саму на себяN раз.

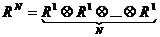Значение N определяется из условия, при котором R^N = R^N-1 , причем N £ n-1.

Матрицаконтрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования, то есть Q = L^T .

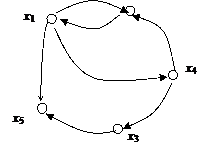
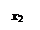Пример.

Рис. 4.4

, , .

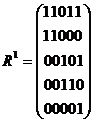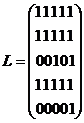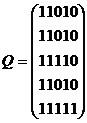Под сильной компонентой (СК) графа G будем понимать подграф G’ графа G максимальной размерности (максимальное число вершин), являющийся сильно связным графом, который не содержится в любом другом сильном подграфе графа G. Ориентированный граф G=(X,F) является сильно связным, если для любой пары вершин (x_i, x_j) существует хотя бы один путь как из x_i ® x_j, так и наоборот из x_j ® x_i.

Сильные компоненты произвольного графа G могут быть найдены в результате поэлементного логического перемножения матриц достижимости и контрдостижимости. Номера столбцов в i-й строке, для которых элемент матрицы равен 1, соответствуют номерам вершин, входящих в данную сильную компоненту. В нашем случае получим

.

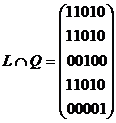Для рассмотренного выше графа (рис. 4.4) получим три сильные компоненты: CK_x1={x₁, x₂, x₄}, CK_x2= {x₃}, CK_x3= {x₅}.

На сильных компонентах, как на вершинах, может быть построен новый граф G*=(X*, F*) – который называется конденсациейграфа G. Каждая его вершина отображает множество вершин, соответствующих одной из сильных компонент исходного графа G, а дуга (x_x^*,x_h^*) существует в G* тогда и только тогда, когда в графе G существует дуга (x_i,x_j) такая, что х_iÎСКх_x, а х_jÎ СКх_h.

Для исходного графа конденсацией будет граф, состоящий из 3-х вершин (рис. 4.5).

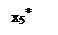
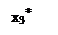
Рис. 4.5.

Базовым множеством графа G называется такое множество В вершин этого графа, из которых достижима любая вершина графа и которое является минимальным в том смысле, что не существует его подмножества, обладающего таким же свойством достижимости.

Доминирующим множеством вершин SÍX графа G=(X,F) называется такое множество вершин, что для каждой вершины х_jÏS существует дуга (путь длиной 1), идущая от некоторой вершины множества S к данной вершине х_j.

Задача нахождения базового и доминирующего множеств в графе сводится к определению такого множества вершин, из которых достижима любая вершина графа (но за различное число шагов). Для этого целесообразно использовать матрицы достижимости и смежности соответственно.

Задача определения минимального доминирующего множества эквивалентна задаче нахождения минимальной ДНФ на импликантной матрице (см. работу №2 настоящего руководства), т.е.такого наименьшего множества строк, что каждый столбец содержит единицу, хотя бы в одной из этого множества строк. Поиск минимального доминирующего множества осуществляется на матрице R¹ достижимости не более чем за один шаг. Таким минимальным доминирующим множеством для графа на рис. 4.4 является множество, состоящее из вершин x₁, x₃ или x₁, x₄ .

Базовое множество определяется аналогично. Но, при этом, в отличие от определения доминирующего множества, задача решается не на матрице R¹, а на матрице достижимости L.

В случае графа большой размерности для поиска базового множества целесообразно сначала найти конденсацию графа, затем базу конденсации, и только затем базу исходного графа, выбирая по одной вершине из каждой сильной компоненты, входящей в базу конденсации. Размерность задачи в этом случае существенно снижается.

Для графа на рис. 4.4 базовым множеством будут вершины или x₁, или x₂, или x₄, (одна из вершин, входящих в сильную компоненту CK_x1={x₁, x₂, x₄}, соответствующую базе конденсации графа G* – вершине x₁^* ).

Для нахождения базовых и доминирующих множеств могут использоваться алгоритмы нахождения ТДНФ и МДНФ из работы №2 настоящего руководства.

Варианты заданий для поиска гамильтонова и эйлерова пути в графе, а также компонент связности графа приведены в Приложении. Для нахождения сильных компонент, базового и доминирующего множеств использовать варианты заданий для поиска ГП в графе.

Контрольные вопросы

1. Что такое Гамильтонов путь? Как определить по матрице смежности начальные и конечные вершины Гамильтонова пути в графе?

2. Какое максимальное число классов эквивалентности может быть в графе?

3. Чему равно число Гамильтоновых путей в насыщенном графе?

4. Что такое связный граф? Как найти связные подграфы в неориентированном графе.

5. Что такое Эйлеров путь? Во всяком ли связном графе существует ЭП?

6. Как по матрице смежности неориентированного графа определить существование ЭП?

7. Что такое сильная компонента графа?

8. Что такое базовое и доминирующее множества графа?

9. Каковы свойства сильной компоненты, минимального базового и доминирующего множеств?

10. Как находится матрица достижимости и контрдостижимости?

11. Что такое конденсация графа.

12. В чем сходство и различие алгоритмов определения базового и доминирующего множеств?