Понятие производной. Физический и геометрический смысл. Основные правила дифференцирования
Если существует предел отношения приращения функции ∆f к приращению аргумента ∆х при условии, что ∆х→0, то этот предел называют значением производной функции y = f(x) в точке х и обозначают f’(x) или y’, а функцию y = f(x) называют дифференцированной в точке х.
f’(x) – это новая функция, определенная во всех таких точках х, в которых существует указанный выше предел.
Операцию по нахождению производной называются дифференцированием.
Производная y = f(x) в точке х выражает скорость изменения функции в точке х, то есть скорость протекания процесса, описываемого зависимостью y = f(x). В этом состоит физический смысл производной.
Значение производной функции y = f(x) в точке х = а равно угловому коэффициенту касательной к графику функции y = f(x) в точке x = a. В этом состоит геометрический смысл производной.
Основные правила дифференцирования:
С (сonst) = 0 kх = k xn = nxn-1 ex = ex ax = ax ln a ln x =  log a x = log a x = 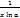 sin x = cos x cos x = - sin x sin x = cos x cos x = - sin x | tg x = 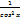 ctg x = ctg x = 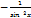 arcsin x = arcsin x = 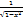 arccos x = - arccos x = - 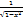 arctg x = arctg x = 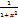 arcctg x = - arcctg x = - 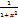 |
Двугранный угол. Пример
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащей одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани. Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
В обыденной жизни мы часто встречаемся с предметами, имеющими форму двугранного угла. Такими предметами являются двускатные крыши зданий, полураскрытая папка, стена комнаты совместно с полом и так далее.
Измерение двугранного угла происходит следующим образом. Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно ребру. Образованный этими лучами угол называется линейным углом двугранного угла. Плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов. Все они равны друг другу.
Градусной мерой двугранного угла называется градусная мера его линейного угла. Двугранный угол может так же быть прямым, острым и тупым в соответствии с его градусной мерой.
3.Найти производную функций 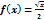
Билет № 12
Основные понятия комбинаторики. Факториал. Задачи на подсчет числа размещений, сочетаний, перестановок.
Комбинаторика – это раздел математики, в котором изучаются задачи выбора элементов из данного множества и размещение этих элементов в каком-либо порядке. Существует насколько способов комбинаторики: перестановка, размещение и сочетание.
Перестановка – операция над упорядоченным порядком из n-элементов, в процессе которых «списочный состав» ряда не меняется, но «места» объектов в этом ряду изменяются от варианта к варианту. Вычисляется по формуле Pn = n!.
Пример: сколько трехзначных чисел модно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Иногда задача заключается в упорядочивании не всех объектов, а лишь некоторой последовательности. Такие последовательности называются размещением. Размещением из n-элементов по m-элементам ( 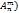 называют конечное упорядоченное множество, содержащие m-элементов выбранных из n-элементов множества А. Вычисляется размещение по следующей формуле:
называют конечное упорядоченное множество, содержащие m-элементов выбранных из n-элементов множества А. Вычисляется размещение по следующей формуле:
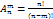 , в которой n – общее количество, а m – количество выбираемых элементов.
, в которой n – общее количество, а m – количество выбираемых элементов.
Данной формулой можно пользоваться, если выбираемые элементы должны быть в определенном порядке.
Пример: сколько можно составить сигналов из 6 флажков различного цвета, если брать по два.
Иногда возникает необходимость не учитывать порядок следования элементов в размещении. Такие последовательности называют сочетанием. Сочетание вычисляется по формуле:
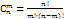 , в которой обозначения букв те же самые, что и в размещении.
, в которой обозначения букв те же самые, что и в размещении.
Пример: скольким количеством способов можно выбрать две детали из ящика, содержащего 10 деталей.
Числа размножений, перестановок и сочетаний связаны между собой следующей формулой 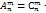 Pn.
Pn.
Факториал числа – обозначается n! – это произведение всех натуральных чисел до n включительно.
