Роль и место математики в современном мире. Математика в медицине.
Роль и место математики в современном мире. Математика в медицине.
Математика – наука о количественных отношениях и пространственных формах действительного мира.
Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Причина проникновения математики в различные отрасли знаний заключается в том, что она предлагает весьма четкие модели для изучения окружающей действительности в отличие от менее общих и более расплывчатых моделей, предлагаемых другими науками. Без современной математики с ее развитым логическими и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.
На первый взгляд медицина и математика могут показаться несовместимыми областями человеческой деятельности. Математика, по общему признанию, является "царицей" всех наук, решая проблемы химии, физики, астрономии, экономики, социологии и многих других наук. Медицина же, долгое время развиваясь "параллельно" с математикой, оставалась практически неформализованной наукой тем самым подтверждая, что "медицина - это искусство".
В настоящее время изучение математики заключается в овладении математическими знаниями и умениями, необходимыми для изучения специальных дисциплин базового уровня, а в требованиях к профессиональной подготовленности специалиста заявлено умение решать профессиональные задачи с использованием математических методов. Такое положение не может не сказываться на результатах математической подготовки медиков. Профессиональная направленность математической подготовки в медицинских образовательных учреждениях должна
обеспечивать повышение уровня математической компетентности студентов-медиков,
осознание ценности математики для будущей профессиональной деятельности,
развитие профессионально значимых качеств и приёмов умственной деятельности,
освоение студентами математического аппарата, позволяющего моделировать, анализировать и решать элементарные математические профессионально значимые задачи,
воспитание потребности в совершенствовании знаний в области математики и её приложений.
Математика очень важна в медицинской статистике. Медицинская статистика должна быть нацелена на решение наиболее выраженных современных проблем в здоровье населения. Основными проблемами здесь, как известно, являются необходимость снижения заболеваемости, смертности и увеличения продолжительности жизни населения. Соответственно, на данном этапе основная информация должна быть подчинена решению этой задачи.
Медицинская наука, конечно, не поддаётся тотальной формализации, как это происходит, скажем, с физикой, но колоссальная эпизодическая роль математики в медицине несомненна. Все медицинские открытия должны опираться на численные соотношения. А методы теории вероятности (учёт статистики заболеваемости в зависимости от различных факторов) - и вовсе вещь в медицине необходимая. В медицине без математики шагу не ступить. Численные соотношения, например, учёт дозы и периодичности приёма лекарств. Численный учёт сопутствующих факторов, таких как: возраст, физические параметры тела, иммунитет и пр.
Стороны оснований правильной треугольной усеченной пирамиды равны 4 дм и 2 дм, а боковое ребро равно 2 пирамиды.дм. Найти площадь боковой и полной поверхности усеченной
Билет № 2
Высота конуса 15 см, а радиус основания равен 8 см. Найти площадь полной поверхности конуса
Билет № 6
Сфера и шар. Площадь сферы
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а данное расстояние – ее радиусом. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы.
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы так же называется центром, радиусом и диаметром шара.
За площадь сферы примем предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.
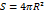
3.Вычислить: 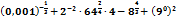
Билет № 7
Взаимное расположение двух прямых в пространстве. Примеры.
В пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, то есть не существует такой плоскости, которая проходит через обе эти прямые.
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямы скрещивающиеся.
Возможны три случая взаимного расположения двух прямых в пространстве:
Прямые пересекаются и имеют одну общую пару
Прямые параллельные
Прямые скрещиваются
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой, и при этом только одна.
3Вычислить: 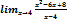
Билет № 11
Двугранный угол. Пример
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащей одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани. Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
В обыденной жизни мы часто встречаемся с предметами, имеющими форму двугранного угла. Такими предметами являются двускатные крыши зданий, полураскрытая папка, стена комнаты совместно с полом и так далее.
Измерение двугранного угла происходит следующим образом. Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно ребру. Образованный этими лучами угол называется линейным углом двугранного угла. Плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов. Все они равны друг другу.
Градусной мерой двугранного угла называется градусная мера его линейного угла. Двугранный угол может так же быть прямым, острым и тупым в соответствии с его градусной мерой.
3.Найти производную функций 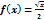
Билет № 12
Основные понятия комбинаторики. Факториал. Задачи на подсчет числа размещений, сочетаний, перестановок.
Комбинаторика – это раздел математики, в котором изучаются задачи выбора элементов из данного множества и размещение этих элементов в каком-либо порядке. Существует насколько способов комбинаторики: перестановка, размещение и сочетание.
Перестановка – операция над упорядоченным порядком из n-элементов, в процессе которых «списочный состав» ряда не меняется, но «места» объектов в этом ряду изменяются от варианта к варианту. Вычисляется по формуле Pn = n!.
Пример: сколько трехзначных чисел модно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Иногда задача заключается в упорядочивании не всех объектов, а лишь некоторой последовательности. Такие последовательности называются размещением. Размещением из n-элементов по m-элементам ( 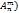 называют конечное упорядоченное множество, содержащие m-элементов выбранных из n-элементов множества А. Вычисляется размещение по следующей формуле:
называют конечное упорядоченное множество, содержащие m-элементов выбранных из n-элементов множества А. Вычисляется размещение по следующей формуле:
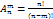 , в которой n – общее количество, а m – количество выбираемых элементов.
, в которой n – общее количество, а m – количество выбираемых элементов.
Данной формулой можно пользоваться, если выбираемые элементы должны быть в определенном порядке.
Пример: сколько можно составить сигналов из 6 флажков различного цвета, если брать по два.
Иногда возникает необходимость не учитывать порядок следования элементов в размещении. Такие последовательности называют сочетанием. Сочетание вычисляется по формуле:
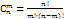 , в которой обозначения букв те же самые, что и в размещении.
, в которой обозначения букв те же самые, что и в размещении.
Пример: скольким количеством способов можно выбрать две детали из ящика, содержащего 10 деталей.
Числа размножений, перестановок и сочетаний связаны между собой следующей формулой 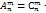 Pn.
Pn.
Факториал числа – обозначается n! – это произведение всех натуральных чисел до n включительно.
Таблица производных основных элементарных функций.
Если существует предел отношения приращения функции ∆f к приращению аргумента ∆х при условии, что ∆х→0, то этот предел называют значением производной функции y = f(x) в точке х и обозначают f’(x) или y’, а функцию y = f(x) называют дифференцированной в точке х.
f’(x) – это новая функция, определенная во всех таких точках х, в которых существует указанный выше предел.
Производные основных элементарных функций:
С = 0 x = 1 x2 = 2x 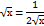 xn = nxn-1 ex = ex ax = ax ln a ln x = xn = nxn-1 ex = ex ax = ax ln a ln x =  | log a x = 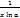 sin x = cos x cos x = - sin x tg x = sin x = cos x cos x = - sin x tg x = 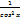 ctg x = ctg x = 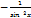 |
Первообразная функции. Таблица первообразных элементарных функций. Основное свойство первообразной.
Функцию y = F(x) называют первообразной функции y = f(x) на промежутке х, если для любого х из Х выполняется равенство F’(x) = f(x).
Если F(x) первообразная для функции y = f’(x) на промежутке х, то у функции y = f(x) бесконечно много первообразных и все эти первообразные имеют вид F(x) + C, где С – любое действительное число.
Операцию отыскания первообразной называются операцией обратной дифференцированию.
| Функция | Первообразная | Функция | Первообразная |
| k | kx + C | cos x | sin x |
| xr | 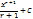 | 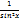 | -ctg x |
 | ln x + C | 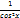 | tg x |
| ex | ex + C | 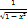 | arssin x |
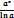 | Ax | 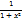 | arctg x |
| sin x | cos x |
Свойства первообразных:
Первообразная суммы равная сумме первообразных.
F (x) + H (x) = f (x) + h (x)
Постоянный множитель можно вынести за знак первообразной.
f (kx) = kF(x)
Если F(x) первообразная для f(x), а k и b – постоянные, причем k ≠ 0, то 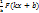 первообразная для f(kx+b).
первообразная для f(kx+b).
3.Исследовать функцию 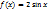 и построить ее график.
и построить ее график.
Билет № 17
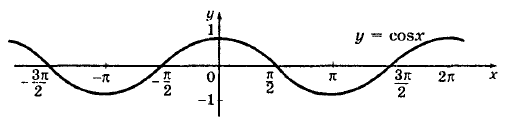
1.Функция y=cos(x), ее свойства и график.
Область определения функции – множество всех действительных чисел.
Область значения – отрезок [-1; 1].
Функция периодическая с основным периодом 2π
Функция убывает на промежутках [2πn; π + 2πn] и возрастает на промежутках [- π + 2π; 2πn], где n принадлежит множеству целых чисел.
Призма. Объем призмы.
Многогранник составленный из двух равных многоугольников (оснований), расположенных в параллельных плоскостях и n-параллелограммов (боковых граней) называется призмой. Отрезки боковых граней называются боковыми ребрами призмы. Ребра призмы равны и параллельных.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниями, то призма называется прямой. В противном случае наклонной. Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если ее основания правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.
Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
Sполн. = Sбок + 2Sосн.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Sбок = P·h.
Объем прямой призмы равен произведению площади основания на высоту.
V = S·h.
3.Упростить выражение 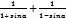 .
.
Билет № 21
1.Тригонометрическое уравнение вида 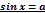 .
.
Формула для корней уравнения sin(x) = a, где -1≤ а ≤ 1, имеет вид: x = (-1)k + πk.
Цилиндр. Объем цилиндра.
Цилиндром (круговым цилиндром) называется тело, состоящее из двух кругов (оснований цилиндра)совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований.
Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра, такое сечение называется осевым. Площадь такого сечения равна площади прямоугольника, которая равна
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение. Такое сечение называется сечением параллельным основанию.
Объем цилиндра равен числу π умноженному на квадрат радиуса одного из оснований и умноженного на высоту цилиндра.
V = πR2h.
3.Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметром 18 м и высотой 7 м, если плотность нефти равна 0,85 г/см3
Билет № 22
1.Тригонометрическое уравнение вида 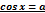 .
.
Формула для корней уравнения cos(x) = a, где -1≤ а ≤ 1, имеет вид: 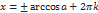 .
.
Пирамида. Объем пирамиды.
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину (вершину пирамиды) – точку пересечения отрезков (боковых ребер), соединяющих ее с вершинами основания.
Высотой пирамиды называется перпендикуляр, опущенный из ее вершины на плоскость основания.
В зависимости от многоугольника, являющегося основанием, пирамида может быть: треугольной, четырех угольной, пяти угольной, n-угольной.
Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота проходит через основания. Все боковые ребра правильной пирамида равны; все боковые грани – равнобедренные треугольники. Высота боковой грани правильной пирамиды называется апофемой.
Тело, ограниченное сечением, проведенным в пирамиде параллельно основанию, основанием пирамиды, и заключенной между ними боковой поверхностью, называется усеченной пирамидой.
Объем пирамиды равен  площади основания умноженной на высоту.
площади основания умноженной на высоту.
3.Найти объем пирамиды с высотой h=2м, если ее основанием служит квадрат со стороной 3м.
Билет № 23
1.Тригонометрическое уравнение вида 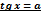 .
.
Формула для корней уравнения tg(x) = a имеет вид: x = arctg a + πk.
Конус. Объем конуса.
Конусом (круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с т очками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Осью прямого конуса называется прямая, содержащая его высоту.
Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым. Площадью является площадь треугольника, которая равна половине произведения основания треугольника на его высоту. Основание данного треугольника будет равно диаметру основания конуса.
Если секущая плоскость перпендикулярна к оси конуса и параллельна его основанию, то сечение конуса представляет собой круг и называется сечением, параллельным основанию. Площадь такого сечения равна площади круга.
Для кругового и усеченного конуса имеются разные формулы объема.
Для кругового конуса 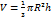 .
.
Для усеченного конуса 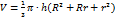 .
.
.3.Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили 2 ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает?
Билет № 24
1.Тригонометрическое уравнение вида 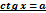 .
.
Формула общего решения уравнения ctg x = a при любом действительном а имеет вид x = arcctg a + πn.
Роль и место математики в современном мире. Математика в медицине.
Математика – наука о количественных отношениях и пространственных формах действительного мира.
Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Причина проникновения математики в различные отрасли знаний заключается в том, что она предлагает весьма четкие модели для изучения окружающей действительности в отличие от менее общих и более расплывчатых моделей, предлагаемых другими науками. Без современной математики с ее развитым логическими и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.
На первый взгляд медицина и математика могут показаться несовместимыми областями человеческой деятельности. Математика, по общему признанию, является "царицей" всех наук, решая проблемы химии, физики, астрономии, экономики, социологии и многих других наук. Медицина же, долгое время развиваясь "параллельно" с математикой, оставалась практически неформализованной наукой тем самым подтверждая, что "медицина - это искусство".
В настоящее время изучение математики заключается в овладении математическими знаниями и умениями, необходимыми для изучения специальных дисциплин базового уровня, а в требованиях к профессиональной подготовленности специалиста заявлено умение решать профессиональные задачи с использованием математических методов. Такое положение не может не сказываться на результатах математической подготовки медиков. Профессиональная направленность математической подготовки в медицинских образовательных учреждениях должна
обеспечивать повышение уровня математической компетентности студентов-медиков,
осознание ценности математики для будущей профессиональной деятельности,
развитие профессионально значимых качеств и приёмов умственной деятельности,
освоение студентами математического аппарата, позволяющего моделировать, анализировать и решать элементарные математические профессионально значимые задачи,
воспитание потребности в совершенствовании знаний в области математики и её приложений.
Математика очень важна в медицинской статистике. Медицинская статистика должна быть нацелена на решение наиболее выраженных современных проблем в здоровье населения. Основными проблемами здесь, как известно, являются необходимость снижения заболеваемости, смертности и увеличения продолжительности жизни населения. Соответственно, на данном этапе основная информация должна быть подчинена решению этой задачи.
Медицинская наука, конечно, не поддаётся тотальной формализации, как это происходит, скажем, с физикой, но колоссальная эпизодическая роль математики в медицине несомненна. Все медицинские открытия должны опираться на численные соотношения. А методы теории вероятности (учёт статистики заболеваемости в зависимости от различных факторов) - и вовсе вещь в медицине необходимая. В медицине без математики шагу не ступить. Численные соотношения, например, учёт дозы и периодичности приёма лекарств. Численный учёт сопутствующих факторов, таких как: возраст, физические параметры тела, иммунитет и пр.
