Признаки сходимости числовых рядов с положительными членами.
Числовые ряды
Числовыми рядами называются бесконечная последовательность чисел, соединенных знаком сложения: U1+U2+…+Un+…= 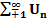 Числа U1U2… называются членами ряда, член Un – общим или n-ым членом ряда, сумма n-первых членов ряда.
Числа U1U2… называются членами ряда, член Un – общим или n-ым членом ряда, сумма n-первых членов ряда.
Sn=U1+U2+…+Un= 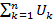 называются частной суммой ряда.
называются частной суммой ряда.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е S= 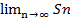
Число S называется суммой ряда. Если конечного предела, последовательности частичного сумм не существует, то ряд называется расходящимся.
Отбрасывание или приписывание к ряду конечного числа членов не влияет на сходимость или расходимость ряда.
Пример Покажем, что ряд 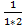 +
+ 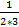 +
+ 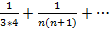 =
= 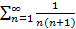 сходится. Возьмем сумму Sn первых n членов ряда. Sn=
сходится. Возьмем сумму Sn первых n членов ряда. Sn= 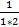 +
+ 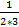 +…+
+…+ 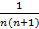 . Слагаемые этой суммы могут быть представлены в виде
. Слагаемые этой суммы могут быть представлены в виде 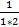 =1-
=1-  ;
; 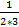 =
=  -
-  ;
; 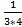 =
=  -
-  ;…;
;…; 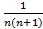 =
=  -
- 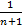 . Поэтому Sn=(1--
. Поэтому Sn=(1--  )+(
)+(  -
- 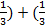 -
-  )+…+(
)+…+( 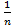 -
- 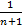 )=1-
)=1- 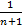 Отсюда следует, что предел последовательности членов числительных сумм данного ряда равен единице.
Отсюда следует, что предел последовательности членов числительных сумм данного ряда равен единице.
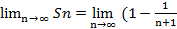 )=1-
)=1- 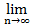
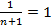 Ряд сходится, его сумма S=1
Ряд сходится, его сумма S=1
Пример 2.
Установим сходятся или расходятся ряды.
1-1+1-1+…+(-1)n-1+…= 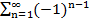
Последовательность его частных сумм имеет вид S1=1, S2=0, S3=1, S4=0… и значит, не сходится ни к какому пределу, поэтому данный ряд расходится.
Пример 3.
Рассмотрим ряд, составленный из элементов геометрической прогрессии:
a +aq+aq2+ aq3+…+ aqn-1+…= 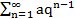 ,a≠0
,a≠0
Частичная сумма Sn этого ряда при q≠1 имеет вид Sn = a +aq+aq2+ aq3+…+ aqn-1= 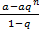 =
= 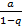 -
- 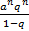
Отсюда:
1. еслиúqú<1, то 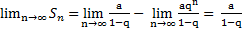 т.е ряды сходятся и его сумма S=
т.е ряды сходятся и его сумма S= 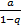
например, при a=1,q=  имеет:
имеет:
S=1+  +
+ 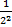 +…
+… 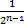 +…=2
+…=2
2. еслиúqú>1, то 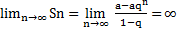 , ряд расходится
, ряд расходится
3. если q=1 ряд принимает вид a+a+a+…a+…
В этом случае: 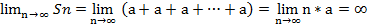 , ряд расходится
, ряд расходится
4. при q=-1 ряд принимает вид a-a+a-a+… Для него Sn =  - –
- – 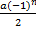 , т.е Sn=0 при n четном и Sn =a при n нечетном. Следовательно,
, т.е Sn=0 при n четном и Sn =a при n нечетном. Следовательно, 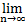 Sn не существует и ряд расходится. Таким образом, ряд является сходящимся приúqú<1 и расходящимся при úqú³1
Sn не существует и ряд расходится. Таким образом, ряд является сходящимся приúqú<1 и расходящимся при úqú³1
2. Необходимое условие сходимости числового ряда.
Если ряд 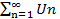 сходится, то предел его общего члена при n→∞ равен нулю
сходится, то предел его общего члена при n→∞ равен нулю 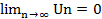 . При нарушении необходимого условия сходимости ряда, т.е если предел общего члена ряда при n→∞, не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
. При нарушении необходимого условия сходимости ряда, т.е если предел общего члена ряда при n→∞, не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
Пример:
Гармонический ряд
1 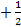 +
+  +…+
+…+  +…=
+…= 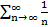 этот ряд расходящийся
этот ряд расходящийся
Пример: обобщенный гармонический ряд
1+ 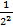 +
+ 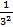 +…+
+…+ 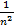 +…=
+…= 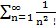
Где α -некоторое число
Этот ряд сходится, если α> 1 и расходится если α≤ 1.
Пример
3+ 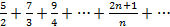
Является расходящимся, поскольку его общий член an= 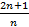 не стремится к нулю.
не стремится к нулю.
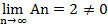
3. Ряды с неотрицательными членами. Достаточные признаки сходимости: признаки сравнения, Даламбера, Коши, интегральный признак.
Признак Даламбера
Пусть для числового ряда 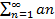 c положительными членами предел отношения последующего члена к предыдущему равен λ:
c положительными членами предел отношения последующего члена к предыдущему равен λ: 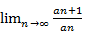 тогда,
тогда,
1. Если λ<1, то ряд сходится
2. Если λ>1, то ряд расходится
3. Если λ=1, то ряд может сходиться, а может и расходится
Примеры:
1. Числовой ряд 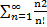 является сходящимся. Для него
является сходящимся. Для него 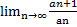 =
= 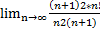 =
= 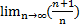 2*
2* 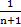
0<1
По признаку Даламбера ряд сходится
2. Числовой ряд 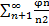 ( все в степени) расходится. Для него
( все в степени) расходится. Для него 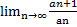 =
= 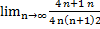 (n+1 в числителе-это степень, а n,2 в знаменателе – это степень)=
(n+1 в числителе-это степень, а n,2 в знаменателе – это степень)= 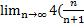 )2 (в степени)=4>1 - По признаку Даламбера ряд расходится
)2 (в степени)=4>1 - По признаку Даламбера ряд расходится
3. Для числового ряда 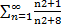 имеем
имеем 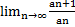 =
= 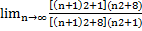 =
= 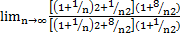
Признак Даламбера не позволяет выяснить вопрос о сходимости ряда, однако этот ряд является расходящимся по необходимому признаку.
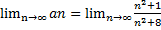 =1≠0
=1≠0
Признак Лейбница.
Знакочередующий ряд 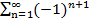 an сходится, если a1>a2>…>an>
an сходится, если a1>a2>…>an> 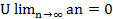
Пример:
Знакочередующий ряд
1- 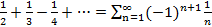 удволетворяет условиям признака Лейбница, поэтому он сходится. Однако ряд из модуля его членов 1-
удволетворяет условиям признака Лейбница, поэтому он сходится. Однако ряд из модуля его членов 1- 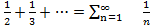 является гармоническим и расходящимся. Таким образом исходный ряд является сходящимся.
является гармоническим и расходящимся. Таким образом исходный ряд является сходящимся.
Тема 2. Степенные ряды
6. Степенные ряды. Интервал, радиус сходимости.
Степенным рядом называется ряд вида
C0+C1X+C2X2+CnXn+…= 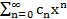 , где cn – некоторые числа, Х-переменная. Коэффициентом степенного ряда называется числа С0,С1,…,Сn,…
, где cn – некоторые числа, Х-переменная. Коэффициентом степенного ряда называется числа С0,С1,…,Сn,…
Пример:
1+х+х2+…+хn+…= 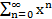 степенной ряд, все его коэффициенты равны 1. При каждом конкретном значении переменной степенной ряд становится числовым рядом, к которому применены все понятия и результаты, в частности, понятия абсолютной сходимости. Областью сходимости степенного ряда называется множества всех значений переменной х, при которых соответствующий числовой ряд сходится.
степенной ряд, все его коэффициенты равны 1. При каждом конкретном значении переменной степенной ряд становится числовым рядом, к которому применены все понятия и результаты, в частности, понятия абсолютной сходимости. Областью сходимости степенного ряда называется множества всех значений переменной х, при которых соответствующий числовой ряд сходится.
Степенной ряд в предыдущим примере является бесконечной суммой членов геометрической прогрессии со знаменателям Х. его частная сумма Sn=s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 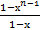 Эта сумма имеет конечный предел
Эта сумма имеет конечный предел 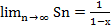 при
при 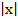 <1. Поэтому область сходимости исходного ряда является интервал (-1;1)
<1. Поэтому область сходимости исходного ряда является интервал (-1;1)
7. Свойства степенных рядов.
Теорема Абеля
a) Если степенной ряд сходится при некотором значении х=х0≠0, то он сходится абсолютно при всех значениях 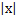 <
< 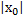
b) Если степенной ряд расходится при х=х1, то он расходится при всех значениях х, таких что 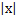 >
> 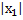
Из теоремы Абеля следует, что существует такоe число R≥0, что при 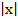 <R сходится, а при
<R сходится, а при 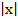 >R ряд расходится. Вопрос о сходимости ряда при х=±R требует дополнительных исследований. Радиусом сходимости степенного ряда называется такое число R≥0, что ряд сходится при
>R ряд расходится. Вопрос о сходимости ряда при х=±R требует дополнительных исследований. Радиусом сходимости степенного ряда называется такое число R≥0, что ряд сходится при 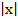 <R и расходится при
<R и расходится при 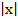 >R. Радиусом сходимости степенного ряда, при Сn≠≠0 находится по формуле
>R. Радиусом сходимости степенного ряда, при Сn≠≠0 находится по формуле
8. Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена.
Формула Маклорина
Формула Маклорина для функции f(x) называется ее формулой Тейлора при x0=0
F(x)=f(0)+ 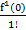 x+
x+ 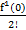 x2+…+
x2+…+ 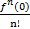 xn+
xn+ 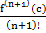 xn+1
xn+1
Где с некоторая точка из интервала (0,x)
9. Применение степенных рядов для приближенных вычислений: интегрирование функций, вычисление пределов.
Числовые ряды
Числовыми рядами называются бесконечная последовательность чисел, соединенных знаком сложения: U1+U2+…+Un+…= 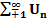 Числа U1U2… называются членами ряда, член Un – общим или n-ым членом ряда, сумма n-первых членов ряда.
Числа U1U2… называются членами ряда, член Un – общим или n-ым членом ряда, сумма n-первых членов ряда.
Sn=U1+U2+…+Un= 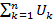 называются частной суммой ряда.
называются частной суммой ряда.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е S= 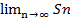
Число S называется суммой ряда. Если конечного предела, последовательности частичного сумм не существует, то ряд называется расходящимся.
Отбрасывание или приписывание к ряду конечного числа членов не влияет на сходимость или расходимость ряда.
Пример Покажем, что ряд 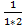 +
+ 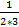 +
+ 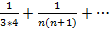 =
= 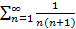 сходится. Возьмем сумму Sn первых n членов ряда. Sn=
сходится. Возьмем сумму Sn первых n членов ряда. Sn= 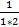 +
+ 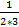 +…+
+…+ 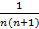 . Слагаемые этой суммы могут быть представлены в виде
. Слагаемые этой суммы могут быть представлены в виде 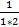 =1-
=1-  ;
; 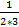 =
=  -
-  ;
; 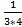 =
=  -
-  ;…;
;…; 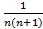 =
=  -
- 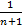 . Поэтому Sn=(1--
. Поэтому Sn=(1--  )+(
)+(  -
- 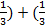 -
-  )+…+(
)+…+( 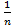 -
- 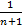 )=1-
)=1- 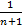 Отсюда следует, что предел последовательности членов числительных сумм данного ряда равен единице.
Отсюда следует, что предел последовательности членов числительных сумм данного ряда равен единице.
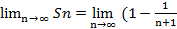 )=1-
)=1- 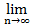
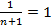 Ряд сходится, его сумма S=1
Ряд сходится, его сумма S=1
Пример 2.
Установим сходятся или расходятся ряды.
1-1+1-1+…+(-1)n-1+…= 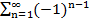
Последовательность его частных сумм имеет вид S1=1, S2=0, S3=1, S4=0… и значит, не сходится ни к какому пределу, поэтому данный ряд расходится.
Пример 3.
Рассмотрим ряд, составленный из элементов геометрической прогрессии:
a +aq+aq2+ aq3+…+ aqn-1+…= 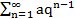 ,a≠0
,a≠0
Частичная сумма Sn этого ряда при q≠1 имеет вид Sn = a +aq+aq2+ aq3+…+ aqn-1= 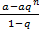 =
= 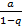 -
- 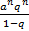
Отсюда:
1. еслиúqú<1, то 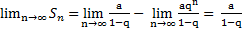 т.е ряды сходятся и его сумма S=
т.е ряды сходятся и его сумма S= 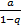
например, при a=1,q=  имеет:
имеет:
S=1+  +
+ 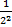 +…
+… 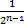 +…=2
+…=2
2. еслиúqú>1, то 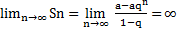 , ряд расходится
, ряд расходится
3. если q=1 ряд принимает вид a+a+a+…a+…
В этом случае: 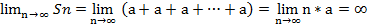 , ряд расходится
, ряд расходится
4. при q=-1 ряд принимает вид a-a+a-a+… Для него Sn =  - –
- – 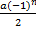 , т.е Sn=0 при n четном и Sn =a при n нечетном. Следовательно,
, т.е Sn=0 при n четном и Sn =a при n нечетном. Следовательно, 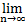 Sn не существует и ряд расходится. Таким образом, ряд является сходящимся приúqú<1 и расходящимся при úqú³1
Sn не существует и ряд расходится. Таким образом, ряд является сходящимся приúqú<1 и расходящимся при úqú³1
2. Необходимое условие сходимости числового ряда.
Если ряд 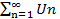 сходится, то предел его общего члена при n→∞ равен нулю
сходится, то предел его общего члена при n→∞ равен нулю 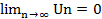 . При нарушении необходимого условия сходимости ряда, т.е если предел общего члена ряда при n→∞, не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
. При нарушении необходимого условия сходимости ряда, т.е если предел общего члена ряда при n→∞, не существует или если он не равен нулю, ряд расходится. Заметим, что если предел общего члена ряда равен нулю, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.
Пример:
Гармонический ряд
1 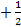 +
+  +…+
+…+  +…=
+…= 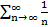 этот ряд расходящийся
этот ряд расходящийся
Пример: обобщенный гармонический ряд
1+ 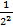 +
+ 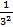 +…+
+…+ 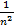 +…=
+…= 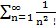
Где α -некоторое число
Этот ряд сходится, если α> 1 и расходится если α≤ 1.
Пример
3+ 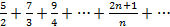
Является расходящимся, поскольку его общий член an= 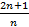 не стремится к нулю.
не стремится к нулю.
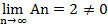
3. Ряды с неотрицательными членами. Достаточные признаки сходимости: признаки сравнения, Даламбера, Коши, интегральный признак.
Признаки сходимости числовых рядов с положительными членами.
Пусть имеется два числовых ряда с положительными членами.
a1+a2+…+an+…(1)
b1+b2+…+bn…(2)
где an>0,bn>,для всех n∈N. Для таких рядов справедливы следующие признаки сходимости.
Признаки сравнения.
Пусть общие члены рядов (1) и (2) (с положительными членами) связаны неравенством an≤bn, для всех n∈N.
Тогда:
1. Если ряд (2) сходится, то и ряд (1) сходится
2. Если ряд (1) расходится, то и ряд (2) расходится
При применении признака сравнения обычно в качестве эталонных рядов рассматриваются следующие ряды.
1. Сумма членов геометрической прогрессии
2. Гармонический ряд
3. Обобщенные гармонический ряд
Пример:
1) 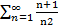 =2+
=2+  +
+  +
+ 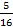 +
+
Является расходящимся, так как его общий член bn= 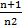 больше общего члена an=
больше общего члена an=  расходящегося гармоничного ряда.
расходящегося гармоничного ряда.
2)Члены числового ряда 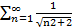 положительны. Сравним их с членами обобщенного гармонического ряда.
положительны. Сравним их с членами обобщенного гармонического ряда. 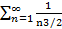 сходится, то по признаку сравнения сходится и сходный ряд.
сходится, то по признаку сравнения сходится и сходный ряд.
Признак Даламбера
Пусть для числового ряда 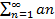 c положительными членами предел отношения последующего члена к предыдущему равен λ:
c положительными членами предел отношения последующего члена к предыдущему равен λ: 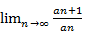 тогда,
тогда,
1. Если λ<1, то ряд сходится
2. Если λ>1, то ряд расходится
3. Если λ=1, то ряд может сходиться, а может и расходится
Примеры:
1. Числовой ряд 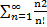 является сходящимся. Для него
является сходящимся. Для него 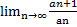 =
= 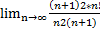 =
= 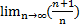 2*
2* 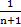
0<1
По признаку Даламбера ряд сходится
2. Числовой ряд 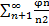 ( все в степени) расходится. Для него
( все в степени) расходится. Для него 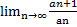 =
= 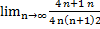 (n+1 в числителе-это степень, а n,2 в знаменателе – это степень)=
(n+1 в числителе-это степень, а n,2 в знаменателе – это степень)= 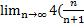 )2 (в степени)=4>1 - По признаку Даламбера ряд расходится
)2 (в степени)=4>1 - По признаку Даламбера ряд расходится
3. Для числового ряда 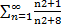 имеем
имеем 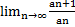 =
= 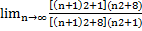 =
= 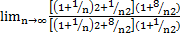
Признак Даламбера не позволяет выяснить вопрос о сходимости ряда, однако этот ряд является расходящимся по необходимому признаку.
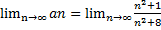 =1≠0
=1≠0
