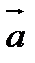Метод Гауса решения систем линейных уравнений

Суть метода сост. в том, что посредством элементарных преобразований система 1 приводится к треугольному или трапецеидальному виду, из которого все реш. сист. Получаются непосредственно.

К элемент. преобр. относятся: 1. Перестановка любых 2-х ур-й системы; 2. умножение любого ур-я системы на отличное от нуля число; 3. прибавление к любому ур-ю системы любого др. ур-я, умноженного на число отличн. от нуля; 4. Вычеркивание ур-я из системы, все коэфф. кот., включая свободный член, равный нулю.

1-й этап. Исключ. неизв.: Пусть в системе 1 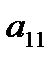≠0, если это не так, добьемся перестановкой ур-й, чтобы 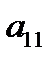≠0. Исключим переменную 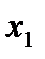из всех ур-й кроме 1-го, для этого из 2-го ур-я отнимаем 1-е умноженное на 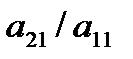. От 3-го ур-я отнимаем 1-е умноженное на 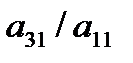и т.д.

Преобр. сист. 1 в сист. 1’ выполнено с помощью 1-го ур-я, наз. разрешающим на данном шаге. Исключалась переменная 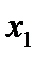, называемая разрешающей, коэфф. 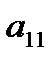при ней наз. разрешающим, столбец коэфф-в 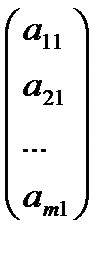при разрешающей переменной – разрешающим столбцом.

В результе может оказаться, что в нескольких последних ур-ях исключены все переменные, т.е. все они имеют вид: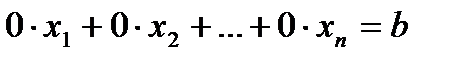

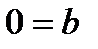
Продолжаем преобр. и придём к одному из случаев:

1) в ходе преобр. получаем уравнение вида 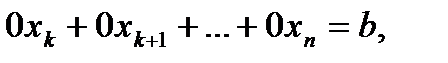где b≠0, и тогда систем несовместна.

2) либо приходим к системе без остаточной части:

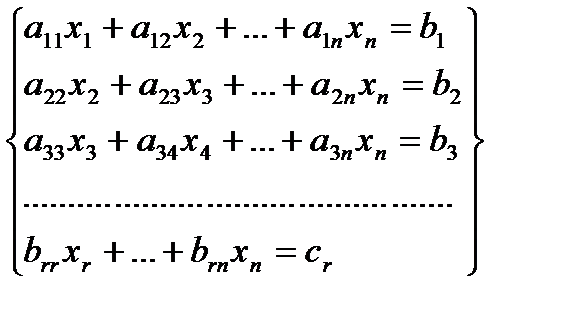
где 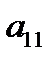, , 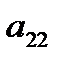,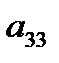…, 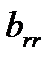отличны от нуля. Возможно уменьшение числа уравнений по сравнению с исходной системой .

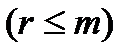Процесс преобр. системы 1 к системе 1’’ называют прямым ходом метода Гауса.

2-й этап. Последовательное нахожд. неизв.

Если в системе 1’’ r=n, то она имеет треугольный вид. Из последнего ур-я 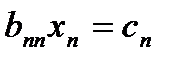находим 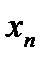, из предпоследнего - 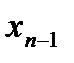и т.д. и наконец из первого - 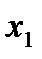и , тем самым, - единственное решение системы 1. Описанный процесс наз. обратным ходом метода Гауса.

Комплексные числа

Исторически понятие КЧ возникло как расширение множества R действит. чисел до такой системы чисел, кот обознач. С и в кот квадратное ур-е 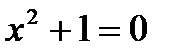имело бы решение.

КЧ наз. число вида 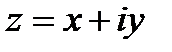, где x и y – действит. числа,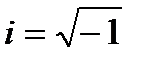

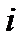- мнимая единица,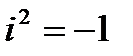

Число х наз. действит. (вещественной) частью КЧ, а y – мнимой. Для этих чисел приняты обозначения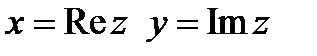

Если y=0, то 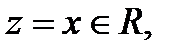если х=0, то 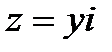наз. числом мнимым.

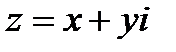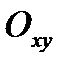При это всякому КЧ соотв. точка y с коорд. плоскостью . Поэтому плоскость наз. комплексной, 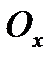- действ. ось, 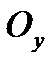- мнимая ось.

Два КЧ 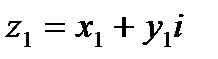и 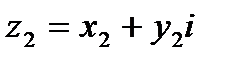равны тогда когда равны их действ. и мнимые части.

КЧ 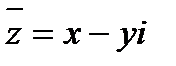наз. комплексосопряженно числу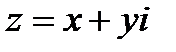

Действия над КЧ:

1.

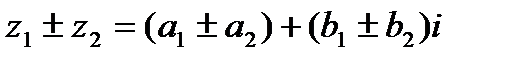
2.

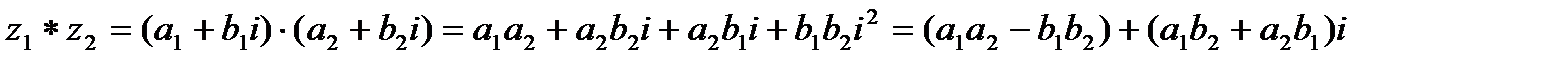
3.

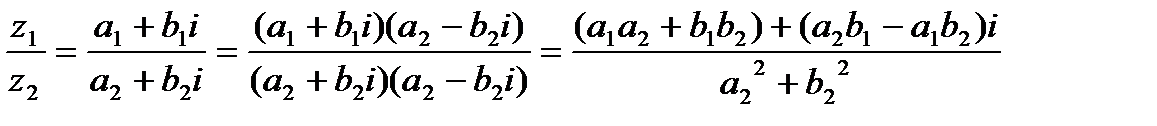
Модулем КЧ 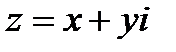наз. длина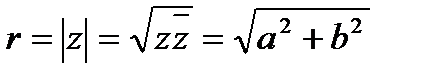

Угол ф между осью абсцисс и вектором ОМ, изображающим комплексное число a+b*I, наз. аргументом КЧ a+b*I.

Понятие вектор. Основные понятия.

Величина, кот. полностью хар-ся своим числовым значением, кот. выражает отношение данной величины к соотв. ед. измерения наз. скалярной величиной или скаляром. Например, в физике m, t, P, V, A. Также физ. величины как сила, скорость, ускорение, перемещение хар-ся не только величиной, но и направлением, наз. вектором.

Вектор представляет собой направленный отрезок. Если его нач. т. А, а кон. – В, то его обозн. .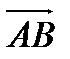

Длинной или модулем вектора 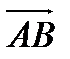наз. длинна отр. .

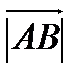Вектор, нач. и конец кот. совпадают, а длина=0, наз. нулевым вектором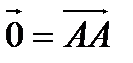

Вектор наз. единичным, если его длина=1. Обозн.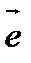

Векторы лежащие на одной или параллельных прямых наз. коллинеарными.

Колл. Векторы могут быть сонаправленными или противоположнонапрвленными.

Един. вектор, направление кот. совпад. с направлением данного вектора а наз. орт вектора а, .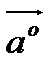

Два вектора наз. равными, если они одинаково направлены и имеют одинаковые длины.

Множество всех векторов = данному вектору 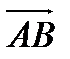наз. свободным вектором и обознач.