Физический смысл производной. Правило дифференцирования произведения.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
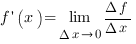
Физический смысл производной.Итак, мы видим, что по аналогии с мгновенной скоростью, производная функции в точке 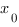 . показывает скорость изменения функции в этой точке.
. показывает скорость изменения функции в этой точке.
Если зависимость расстояния от времени представляет собой функцию 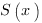 , то, чтобы найти скорость тела в момент времени
, то, чтобы найти скорость тела в момент времени 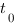 , нужно найти значение производной функции
, нужно найти значение производной функции 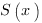 в точке
в точке 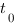 :
:
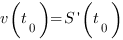
Если функции u = u(x) и v = v(x) дифференцируемы в точке х, то
( u · v ) ' = u '·v + v ' · u.
Доказательство. По определению производной имеем
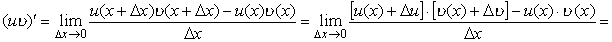
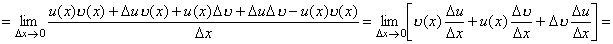
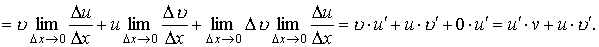
Здесь учтена связь между дифференцируемостью и непрерывностью:
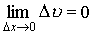 .Правило дифференцирования произведения функций (правило Лейбница):
.Правило дифференцирования произведения функций (правило Лейбница):
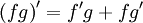
49. Горизонтальные, вертикальные и наклонные асимптоты и их нахождение.Различают вертикальные и наклонные асимптоты (в частности, горизонтальные).Прямаях = аназывается вертикальной асимптотой, если хотя быодин из односторонних пределов
f (а + 0), f (а – 0) равен бесконечности или не существует, то есть в точке х = а функция терпит разрыв второго рода.Асимптотой графика функции называется прямая, к которой неограниченно приближается график функции при 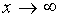 или
или 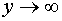 Горизонтальная асимптота — прямая вида
Горизонтальная асимптота — прямая вида 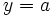 при условии существования предела
при условии существования предела 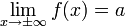 .Наклонная асимптота — прямая вида
.Наклонная асимптота — прямая вида 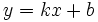 при условии существования пределов
при условии существования пределов
1. 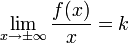
2. 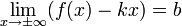
 34. Производная функции. Геометрическое и формальное определение.Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Пусть в некоторой окрестноститочки
34. Производная функции. Геометрическое и формальное определение.Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Пусть в некоторой окрестноститочки 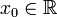 определена функция
определена функция 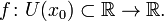 Производной функции называется такое число
Производной функции называется такое число 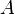 , что функцию в окрестности
, что функцию в окрестности 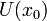 можно представить в виде
можно представить в виде 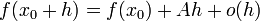 если
если 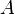 существует. 38.Дифференцирование суперпозиции функции(правилодифференцирования сложной функции).Правило дифференцирования сложной функции:
существует. 38.Дифференцирование суперпозиции функции(правилодифференцирования сложной функции).Правило дифференцирования сложной функции: 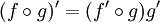 47. Исследование функций с помощью производных первого и второго порядка на максимум и минимум. Пусть в точке х = х1f(x1) = 0 и f(x1) существует и непрерывна в некоторой окрестности точки х1. Теорема.Если f(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f(x1)<0 и минимум, если f(x1)>0. Доказательство. Пусть f(x1) = 0 и f(x1)<0. Т.к. функция f(x) непрерывна, то f(x1) будет отрицательной и в некоторой малой окрестности точки х1. Т.к. f(x) = (f(x)) < 0, то f(x) убывает на отрезке, содержащем точку х1, но f(x1)=0, т.е. f(x) > 0 при х<x1 и f(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум. Для случая минимума функции теорема доказывается аналогично. Если f(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование. 40. Производная степенных функций с натуральным, рациональным и отрицательным показателями. Формула производной степенной функции имеет вид
47. Исследование функций с помощью производных первого и второго порядка на максимум и минимум. Пусть в точке х = х1f(x1) = 0 и f(x1) существует и непрерывна в некоторой окрестности точки х1. Теорема.Если f(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f(x1)<0 и минимум, если f(x1)>0. Доказательство. Пусть f(x1) = 0 и f(x1)<0. Т.к. функция f(x) непрерывна, то f(x1) будет отрицательной и в некоторой малой окрестности точки х1. Т.к. f(x) = (f(x)) < 0, то f(x) убывает на отрезке, содержащем точку х1, но f(x1)=0, т.е. f(x) > 0 при х<x1 и f(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум. Для случая минимума функции теорема доказывается аналогично. Если f(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование. 40. Производная степенных функций с натуральным, рациональным и отрицательным показателями. Формула производной степенной функции имеет вид 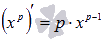 , где показатель степени p – любое действительное число. 41. Производная синуса и косинуса.
, где показатель степени p – любое действительное число. 41. Производная синуса и косинуса. 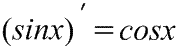 Производная синуса
Производная синуса 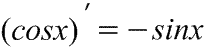 Производная косинуса 39. Обратная функция, её график и производная. Производная логарифмической функции. Пусть функция
Производная косинуса 39. Обратная функция, её график и производная. Производная логарифмической функции. Пусть функция 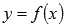 строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения 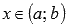 , область значений этой функции
, область значений этой функции 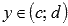 , тогда на интервале
, тогда на интервале 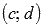 определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция 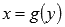 с областью значений
с областью значений 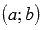 , которая является обратной для
, которая является обратной для 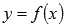 .нахождения обратных функций. Пример(линейные взаимно обратные функции). Найти функцию обратную для
.нахождения обратных функций. Пример(линейные взаимно обратные функции). Найти функцию обратную для 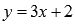 . Решение. Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение
. Решение. Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение 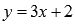 относительно x ).
относительно x ). 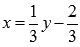 - это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать
- это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать 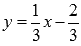 . Таким образом,
. Таким образом, 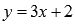 и
и 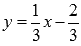 - взаимно обратные функции. График взаимно обратных линейных функций.
- взаимно обратные функции. График взаимно обратных линейных функций. 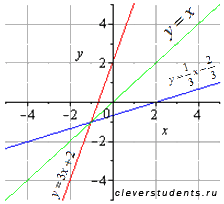 Производная логарифмической функции y = logax определяется выражением
Производная логарифмической функции y = logax определяется выражением 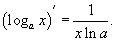
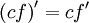 Правило дифференцирования суммы функций:
Правило дифференцирования суммы функций: 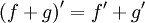 Правило дифференцирования разности функций:
Правило дифференцирования разности функций: 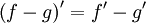 Правило дифференцирования произведения функций (правило Лейбница):
Правило дифференцирования произведения функций (правило Лейбница): 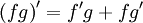 Правило дифференцирования частного функций:
Правило дифференцирования частного функций: 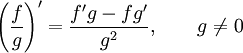 Правило дифференцирования функции в степени другой функции:
Правило дифференцирования функции в степени другой функции: 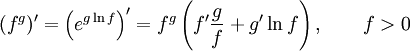 Правило дифференцирования сложной функции:
Правило дифференцирования сложной функции: 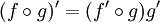 Правило логарифма при дифференцировании функции:
Правило логарифма при дифференцировании функции: 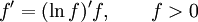 Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Производная постоянной.При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем
Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Производная постоянной.При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем 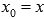 , где x – любое действительное число, то есть, x – любое число из области определения функции
, где x – любое действительное число, то есть, x – любое число из области определения функции 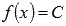 . Запишем предел отношения приращения функции к приращению аргумента при
. Запишем предел отношения приращения функции к приращению аргумента при 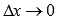 :
: 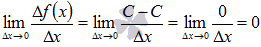 Следует заметить, что под знаком предела получается выражение
Следует заметить, что под знаком предела получается выражение 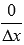 , которое не является неопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю. Таким образом, производная постоянной функции
, которое не является неопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю. Таким образом, производная постоянной функции 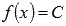 равна нулю на всей области определения. Пример.Найти производные следующих постоянных функций
равна нулю на всей области определения. Пример.Найти производные следующих постоянных функций 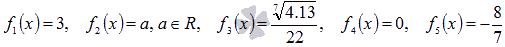 Решение.В первом случае мы имеем производную натурального числа 3, во втором случае нам приходится брать производную от параметра а, который может быть любым действительным числом, в третьем - производную иррационального числа
Решение.В первом случае мы имеем производную натурального числа 3, во втором случае нам приходится брать производную от параметра а, который может быть любым действительным числом, в третьем - производную иррационального числа 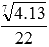 , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби
, в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби 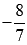 . Ответ:производные всех этих функций равны нулю для любого действительного x (на всей области определения)
. Ответ:производные всех этих функций равны нулю для любого действительного x (на всей области определения) 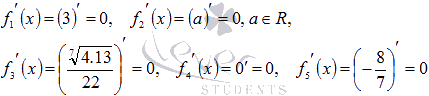 Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.производная суммы равна сумме производных. 1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х0+Δx)+ v(х0+Δx) – (u(х0)+v(х0)) = (u(х0+Δx)-u(х0)) + (v(х0+Δx)-v(х0)) = Δu + Δv 2)
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.производная суммы равна сумме производных. 1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х0+Δx)+ v(х0+Δx) – (u(х0)+v(х0)) = (u(х0+Δx)-u(х0)) + (v(х0+Δx)-v(х0)) = Δu + Δv 2) 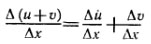 3) Функции u и v дифференцируемы в точке х0, т. е. при Δх→0
3) Функции u и v дифференцируемы в точке х0, т. е. при Δх→0 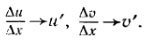 Тогда
Тогда 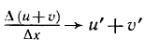 при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’ Лемма. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е. f(х0 + Δх)→f (х0) при Δx→0 Действительно,
при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’ Лемма. Если функция f дифференцируема в точке х0, то она непрерывна в этой точке: Δf→0 при Δx→0, т. е. f(х0 + Δх)→f (х0) при Δx→0 Действительно, 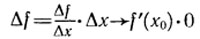 при Δх→0, так как
при Δх→0, так как 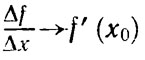 Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х0 + Δx)→f (х0) при Δх→0.
Итак, Δf→0 при Δx→0, т. е. для дифференцируемых функций f (х0 + Δx)→f (х0) при Δх→0. 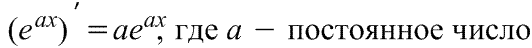 Производная экспоненты. Обычно математики называют так функцию у = ех, где
Производная экспоненты. Обычно математики называют так функцию у = ех, где 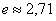 – основание натуральных логарифмов – неперово число;
– основание натуральных логарифмов – неперово число; 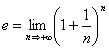 . При этом к её названию часто добавляют прилагательное «основная», чтобы отличить от показательной функции у = ах с положительным действительным основанием а, отличным от единицы. 43.Уравнение касательной к графику функции. Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.y = f ’(x0) · (x − x0) + f (x0) Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции 44. Графики степенных функций ,экспоненты и логарифма. Сравнение их поведения на бесконечности.Степенна́яфу́нкция — функция
. При этом к её названию часто добавляют прилагательное «основная», чтобы отличить от показательной функции у = ах с положительным действительным основанием а, отличным от единицы. 43.Уравнение касательной к графику функции. Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.y = f ’(x0) · (x − x0) + f (x0) Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции 44. Графики степенных функций ,экспоненты и логарифма. Сравнение их поведения на бесконечности.Степенна́яфу́нкция — функция 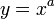
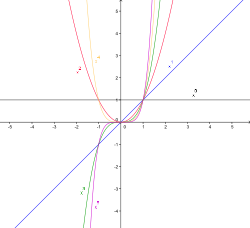
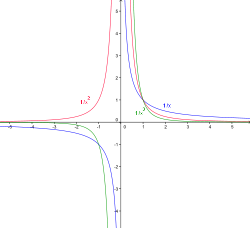 Экспонента — показательнаяфункция
Экспонента — показательнаяфункция 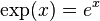 , где e — Число Эйлера (
, где e — Число Эйлера ( 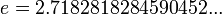 ).
). 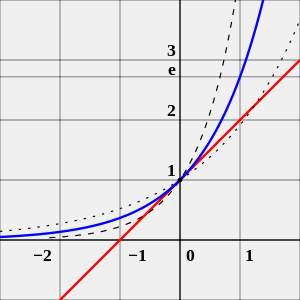
 График экспоненты. Касательная в нуле у функции
График экспоненты. Касательная в нуле у функции 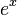 наклонена на
наклонена на 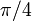 Рядом для примера показаны
Рядом для примера показаны 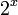 (точками) и
(точками) и 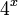 (пунктиром) Логарифм.
(пунктиром) Логарифм. 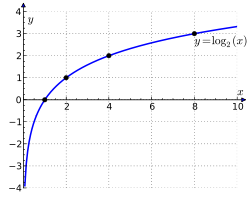 График двоичного логарифма
График двоичного логарифма 45. Правило Лопиталя. Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль 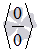 ,бесконечность делить на бесконечность ,бесконечность делить на бесконечность 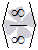 . К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность . К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность 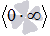 и бесконечность минус бесконечновть и бесконечность минус бесконечновть 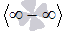 . Дифференцирование функции и нахождение производной является неотъемлемой частью правила Лопиталя, так что рекомендуем обращаться к этому разделу. Формулировка правила Лопиталяcледующая: Если . Дифференцирование функции и нахождение производной является неотъемлемой частью правила Лопиталя, так что рекомендуем обращаться к этому разделу. Формулировка правила Лопиталяcледующая: Если 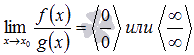 , и если функции f(x) и g(x) – дифференцируемы в окрестности точки , и если функции f(x) и g(x) – дифференцируемы в окрестности точки 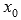 , то , то 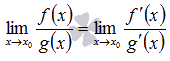 . Пример. Вычислить предел, используя правило Лопиталя . Пример. Вычислить предел, используя правило Лопиталя 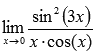 Решение. Подставляем значение Решение. Подставляем значение 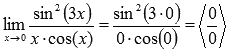 Пределы с неопределенностью данного типа можно находить по правилу Лопиталя: Пределы с неопределенностью данного типа можно находить по правилу Лопиталя: 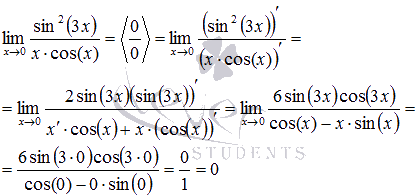 Ответ: Ответ: 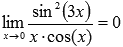 | 46 Производные высших порядков. Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде 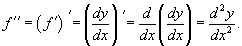 Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f: Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f: 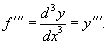 Производные более высокого порядка (если они существуют), определяются как Производные более высокого порядка (если они существуют), определяются как 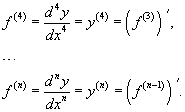 Для нахождения производных высшего порядка можно использовать следующие формулы: Для нахождения производных высшего порядка можно использовать следующие формулы: 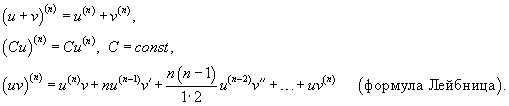 В частности, для производной второго и третьего порядка формула Лейбница принимает вид В частности, для производной второго и третьего порядка формула Лейбница принимает вид 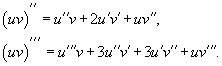 |
36. Физический смысл производной функции.
Если положение точки при её движении по числовой прямой задаётся функцией S = f(t), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.
Правило дифференцирования произведения функций.
Производная (дифференциал) произведения двух дифференцируемых функций равна
сумме произведений производной (дифференциала) первого сомножителя на второй
и производной (дифференциала) второго сомножителя на первый т.е.
(u·v)/=u/v+v/u
37.Правило дифференцирования частного функций.
Производная (дифференциал) дроби (частного двух дифференцируемых функций)
равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а
числитель представляет собой разность между произведением знаменателя данной
дроби на производную (дифференциал) ее числителя и произведения числителя на
производную (дифференциал) знаменателя.
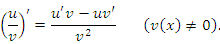
38.Правило дифференцирования сложной функции.
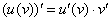
(дифференцирование сложной функции). Пусть
функция x = f(t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f(t). Тогда сложная функция y = f(f(t)) дифференцируема в точке t, причем справедлива формула (f(f(t)))' = f'(x)f'(t). (3)
Доказательство. Зададим x = f(t) отличное от нуля приращение D t. Этому приращению отвечает приращение D x = f (t+D t)-f (t) функции x = f(t). Приращению D x отвечает приращение D y = f(x+ D x)-f(x). Так как функция y = f(x) дифференцируема, то ее приращение D y представимо в виде (1):
D y =f'(x)D x +a (D x) D x,
гдеlimD x® 0a (D x ) = 0. Поделив данное выражение на D t № 0, будем иметь:
D y/D t=f'(x)D x/D t+ a (D x)D x/D t.
Из дифференцируемости функции x = f (t) в точке t вытекает, что
limD t® 0D x/D t = f'(t).
Отметим, что из дифференцируемости функции x = f(t) следует, что D x® 0 при D t® 0. Следовательно, limD t® 0a (D x) =0. Таким образом, получим необходимую формулу (3).
Пример 5. Найтиy', еслиy = 5cosxy' = 5cosx(-sinx)ln 5=-5cosxsinxln 5.
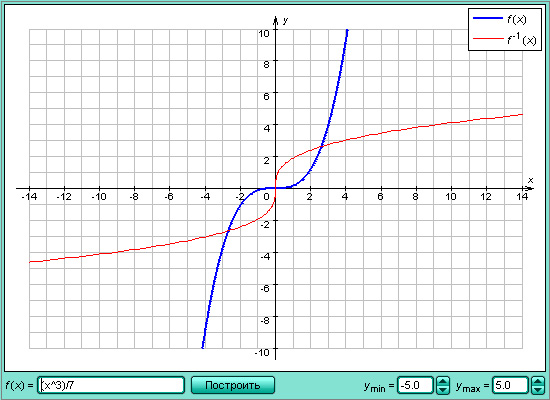
39. Обратная функция.
Пусть задана функция y = f (x), Тогда каждому числу соответствует единственное число Иногда приходится по значению функции y0 находить значение аргумента x0, то есть решать уравнение f (x) = y0 относительно x. Это уравнение может иметь несколько или даже бесконечное количество решений (решениями являются абсциссы всех точек, в которых график y = f (x) пересекается с прямой y = y0).
Если функция f такова, что каждому значению соответствует только одно значение то эту функцию называют обратимой. Для такой функции уравнение y = f (x) можно при любом y однозначно разрешить относительно x, то есть каждому соответствует единственное значение Это соответствие определяет функцию, которую называют обратной к функции f и обозначают символом f–1.
Пусть g = f–1. Тогда:
D (g) = E (f), E (g) = D (f);
для любого g (f (x)) = x,
для любого f (g (x)) = x;
графики функций y = f (x) и y = g (x) симметричны друг другу относительно прямой y = x.