Общая схема исследования функции и построения ее графика

Одна из возможных схем исследования функции и построения ее графика разлагается на следующие этапы решения задачи.

Элементарное исследование

1. Найти область определения функции.

2. Найти точки разрыва функции. Их характер. Вертикальные асимптоты.

3. Исследовать функцию на симметричность (определить четность и нечетность функции) и периодичность.

4. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с осями координат. Найти интервалы знакопостоянства.

5. Вычислить предельные значения функции в ее граничных точках.

6. Выяснить существование наклонных асимптот.

Исследование функции по первой производной

7. Найти решение уравнений .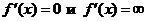

8. Критические точки, исследовать с помощью достаточного условия экстремума, определить вид экстремума. Вычислить значения функции в точках экстремума.

9. Найти интервалы монотонности функции.

Исследование функции по второй производной

10. Найти решение уравнений .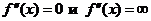

11. Критические точки исследовать с помощью достаточного условия. Вычислить значения функции в точках перегиба.

12. Найти интервалы выпуклости вниз и вверх графика функции.

13. Построить график функции.

Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом.

График функции лучше всего строить в таком порядке:

1. Построить все асимптоты, если они есть.

2. Нанести на график характерные точки: точки пересечения с осями координат, точки, в которых есть экстремум, точки перегиба.

Построение проводить в интервалах непрерывности с учетом проведенных исследований.

Пример 13. Провести полное исследование функции 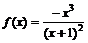и построить ее график.

▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

· Область определения функции. 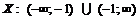. Точка разрыва: .

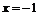· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

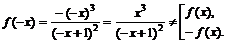Функция общего вида.

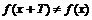. Функция не периодична.

· Выясним существование асимптот. В точке 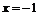функция имеет разрыв II рода, ибо,

; ,

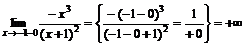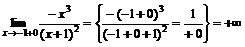в остальных точках она непрерывна. Прямая 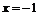является вертикальной асимптотой.

Найдем наклонные асимптоты .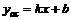

Слева .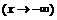

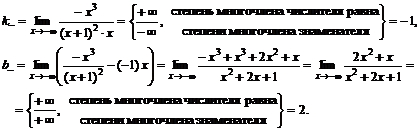
Уравнение наклонной асимптоты слева .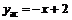

Справа .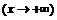

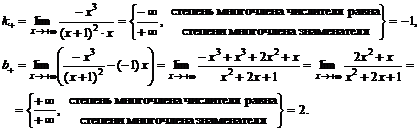
Уравнение наклонной асимптоты справа .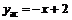

· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью : .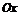

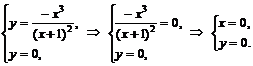
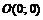Точки пересечения с осью : .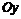

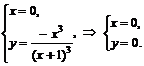
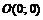Промежутки знакопостоянства

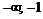		–1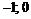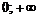
	+		+		–

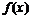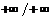II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

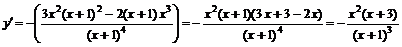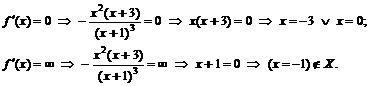
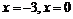к. т. I.

Область определения функции разобьем на интервалы 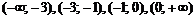и определим знак 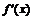в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 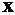) с указанием поведения функции на этих интервалах занесем в таблицу:

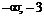		–3		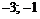–1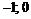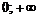
	–		+		–		–

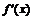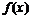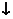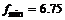Так как функция в точке 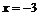определена и непрерывна и при переходе через нее 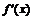меняет знак с минуса на плюс, то в этой точке минимум, причем .

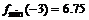III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

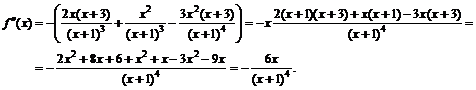
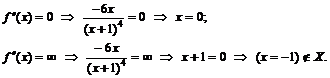
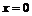к. т. II.

Область определения функции разобьем на интервалы 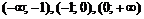и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

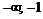		–1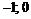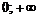
	+		+		–

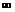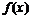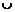При переходе через точку 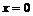вторая производная меняет знак, следовательно, это точка перегиба функции, причем 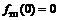. Точка 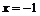не является точкой перегиба.

Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼

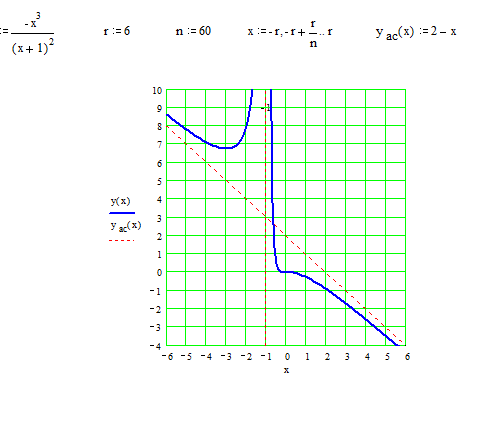Пример 14. Провести полное исследование функции 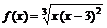и построить ее график.

▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

· Область определения функции. .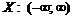

· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

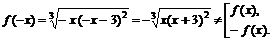Функция общего вида.

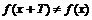. Функция не периодична.

· Выясним существование асимптот.

Вертикальных асимптот нет, так как нет точек разрыва.

Найдем наклонные асимптоты .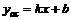

Слева .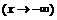

,

.

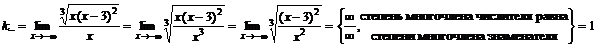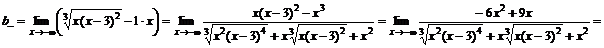
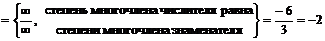Уравнение наклонной асимптоты слева .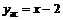

Справа .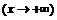

,

.

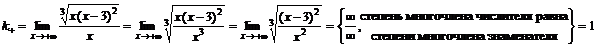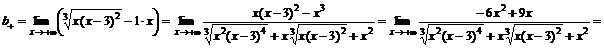
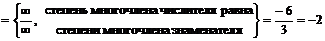Уравнение наклонной асимптоты справа .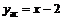

· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью :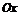

.

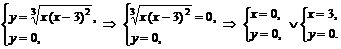
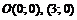Точки пересечения с осью : .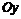

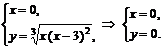
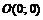Промежутки знакопостоянства

	–		+		+

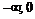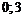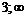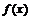II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

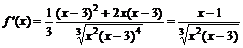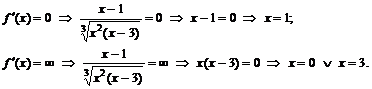
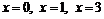к. т. I.

Область определения функции разобьем на интервалы 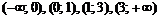и определим знак 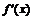в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 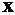) с указанием поведения функции на этих интервалах занесем в таблицу:

	+		+		–		+

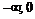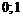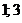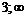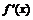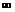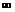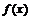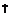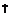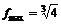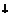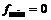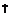Так как функция в точке 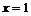определена и непрерывна и при переходе через нее 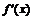меняет знак с плюса на минус, то в этой точке максимум, причем 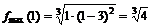. В точке 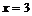функция определена и непрерывна и при переходе через нее 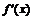меняет знак с минуса на плюс, следовательно, в этой точке минимум, причем .

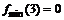III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

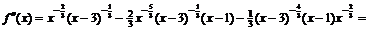
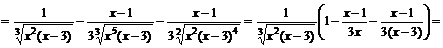
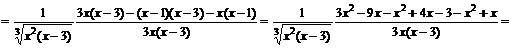
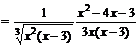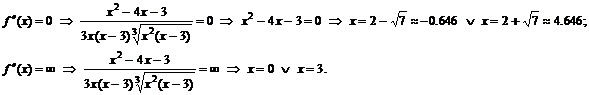
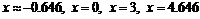к. т. II.

Область определения функции разобьем на интервалы 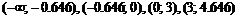, 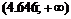и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

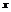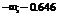		–0.646		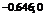		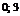		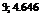4.646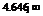
	–		+		–		–		+

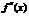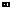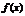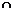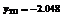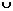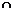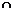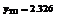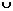При переходе через точки вторая производная меняет знак, следовательно, это точки перегиба функции, причем

,

.

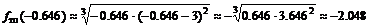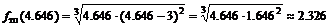Точки перегиба: .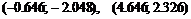

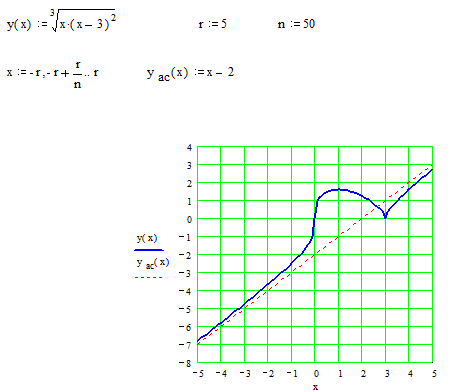
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼

Пример 15. Провести полное исследование функции 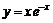и построить ее график.

▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

· Область определения функции. .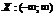

· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

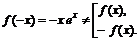Функция общего вида.

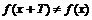. Функция не периодична.

· Выясним существование асимптот.

Вертикальных асимптот нет, так как нет точек разрыва.

Найдем наклонные асимптоты .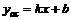

Слева .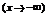

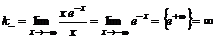. Слева наклонной асимптоты нет.

Справа .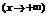

,

.

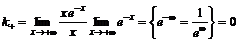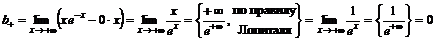Справа горизонтальная асимптота: .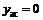

· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью : .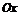

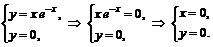
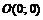Точки пересечения с осью : .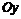

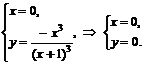
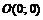Промежутки знакопостоянства

	–		+

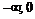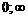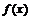II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

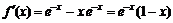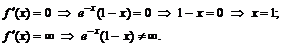
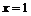к. т. I.

Область определения функции разобьем на интервалы 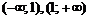и определим знак 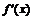в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 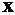) с указанием поведения функции на этих интервалах занесем в таблицу:

	+		–

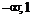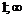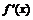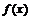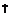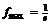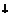Так как функция в точке 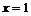определена и непрерывна и при переходе через нее 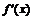меняет знак с плюса на минус, то в этой точке максимум, причем .

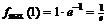III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

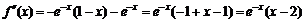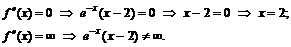
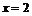к. т. II.

Область определения функции разобьем на интервалы 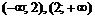и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

	–		+

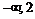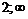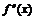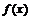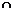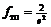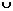При переходе через точку 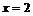вторая производная меняет знак, следовательно, это точка перегиба функции, причем 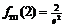. Точка перегиба: .

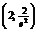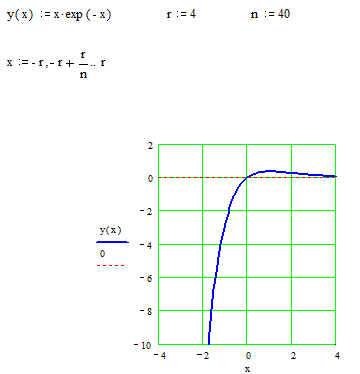
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼

Пример 16. Провести полное исследование функции 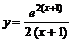и построить ее график.

▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

· Область определения функции 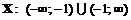. Точка разрыва: .

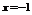· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

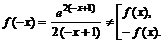Функция общего вида.

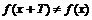. Функция не периодична.

· Выясним существование асимптот. В точке 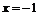функция имеет разрыв II рода, ибо,

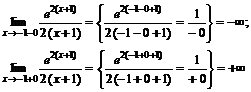
в остальных точках она непрерывна. Прямая 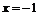является вертикальной асимптотой.

Найдем наклонные асимптоты .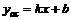

Слева .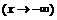

,

.

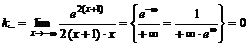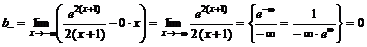Уравнение горизонтальной асимптоты слева: .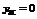

Справа .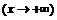

.

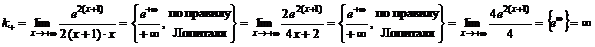Справа наклонной асимптоты нет.

· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью 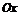: 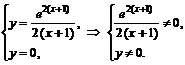Точек пересечения с осью 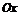нет.

Точки пересечения с осью 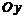: 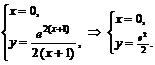Точка пересечения с осью : .

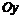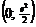Промежутки знакопостоянства

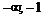		–1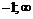
	–		+

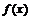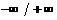II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

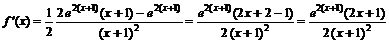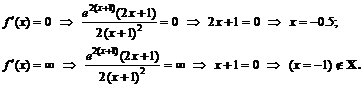
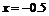к. т. I.

Область определения функции разобьем на интервалы 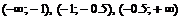и определим знак 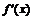в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 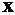) с указанием поведения функции на этих интервалах занесем в таблицу:

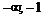		–1		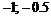–0.5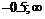
	–		–		+

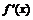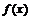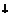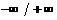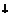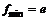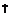Так как функция в точке 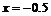определена и непрерывна и при переходе через нее 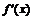меняет знак с минуса на плюс, то в этой точке минимум, причем .

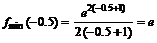III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

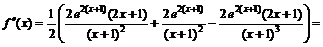
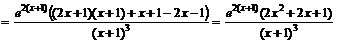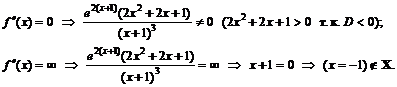к. т. II нет.

Область определения функции разобьем на интервалы 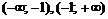и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

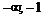		–1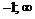
	–		+

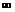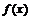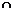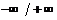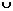Точек перегиба нет.

Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

Пример 17. Провести полное исследование функции 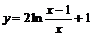и построить ее график.

▲Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

· Область определения функции. .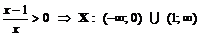

· Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

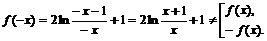Функция общего вида.

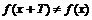. Функция не периодична.

· Выясним существование асимптот. Вертикальная асимптота может существовать лишь на конечных границах области определения. Найдем

.

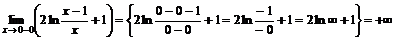Значит, прямая 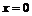– вертикальная асимптота.

Найдем

.

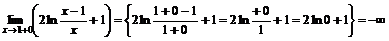Следовательно, прямая 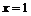– вертикальная асимптота.

Найдем наклонные асимптоты .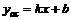

Слева .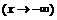

,

.

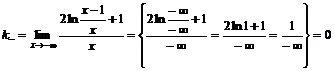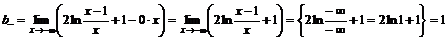Уравнение горизонтальной асимптоты слева .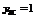

Справа .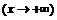

,

.

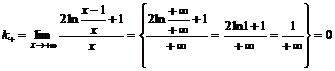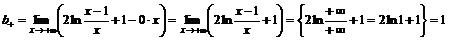Уравнение горизонтальной асимптоты справа .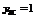

· Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью :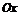

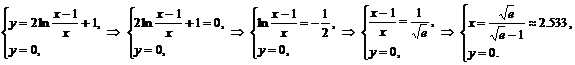
Точка пересечения с осью : .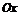

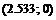Точек пересечения с осью 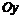нет.

Промежутки знакопостоянства

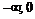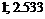					2.533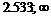
	+			–		+

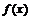II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

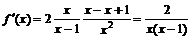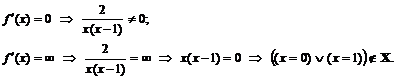к. т. I нет.

Область определения функции разобьем на интервалы 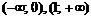и определим знак 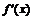в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом 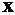) с указанием поведения функции на этих интервалах занесем в таблицу:

	+			+

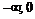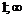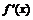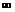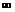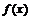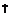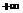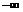Экстремумов нет.

III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

;

.

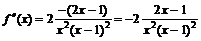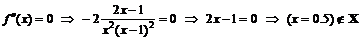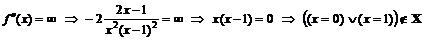К. т. II нет.

Область определения функции разобьем на интервалы 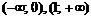и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

	+			–

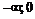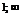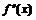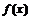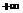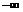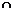Точек перегиба нет.

Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼
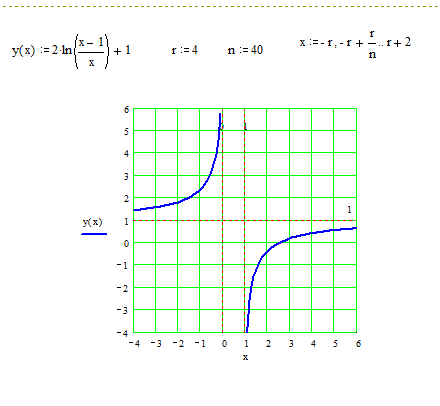