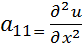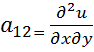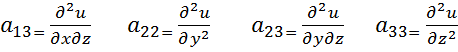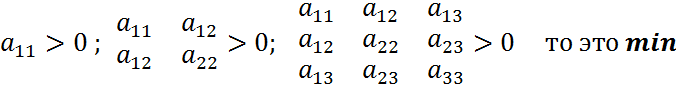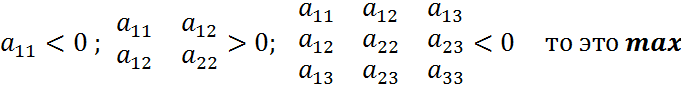Частные производные первого порядка фнп

Z=(xy), функция где есть Х и У, нужно взять производную по Х, и производную по У т.е. 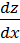и .

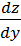НЕЯВНО ЗАДАННЫЕ ФНП:

Находится Y_x’ = 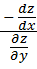= 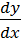, находится отношение производной по Х и производной по У.

ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШЕГО ПОРЯДКА ФНП

Частные производные от производных первого порядка функции наз. частными производными второго порядка. Они обозначаются:

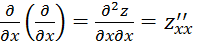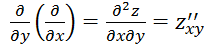и и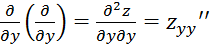

Дифференциалы I и II порядка:

Функция называется дифференцируемой, если ее приращение может быть представлено в виде суммы линейной функции от приращений аргументов 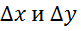. Главная часть приращения дифференцируемой функции 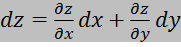называется полным дифференциалом функции z(dx= )

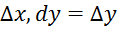Выражения 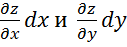называют частными дифференциалами.

Для второго порядка: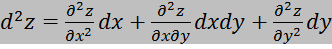

Для трех переменных: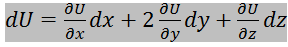

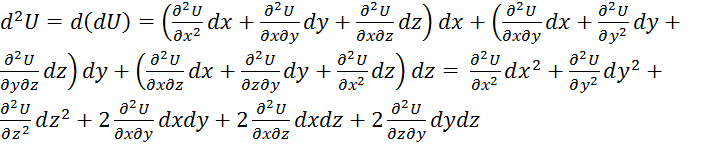
КАСАТЕЛЬНАЯ И НОРМАЛЬ

Касательная -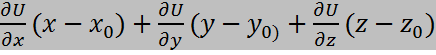

Нормаль -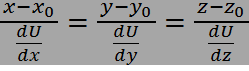

ЭКСТРЕМУМ ФНП

1) находим частные производные от функции

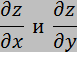
2) Составляем систему уравнения

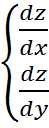Выделяем Х и У, х=… и у=…

Подставляем х и у в систему находим соответствующие точки (х₁;у₁) и (х₂;у₂) т.е. М₁(х₁;у₁) и М₂(х₂;у₂)

3) Вычислим вторую производную

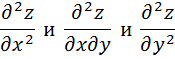
4) Рассматриваем точки М₁(х₁;у₁) и М₂(х₂;у₂) …..

Подставляя значения точек М_n(х_n;у_n) во II производную

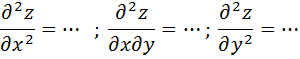
5) Составляем матрицу А со значениями второй производной:

s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 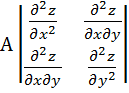затем находим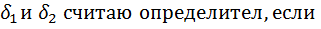

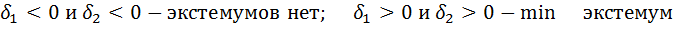
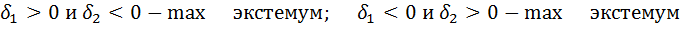
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ

Z=x³-3x³y+3xy²+1 и точки M(3;1) и М₁(6;5)

1) Находим l=(вектор)MM₁={3;4}

2) Находим длину |l|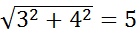

3) l₀={ 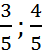} где, x=cosα, y=cosβ

4) Находим первые производные 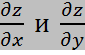и подставляем в место х и узначения точки M₀

5) И все найденное подставляем в формулу:

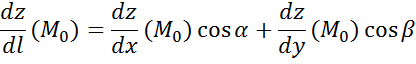
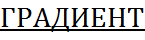
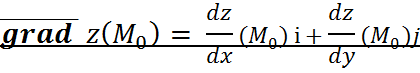
Нахождение ДИФФЕРЕНЦИАЛА.

1. Сначала находим производную

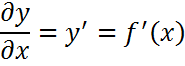
2. Затем придел производной

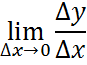
3. Потом и сам дифференциал

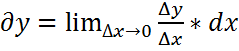
ФОРМУЛА ТЕЙЛОРА

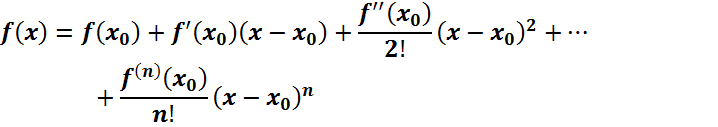
ФОРМУЛА ТЕЙЛОРА ДЛЯ 3х ПЕРЕМЕННЫХ

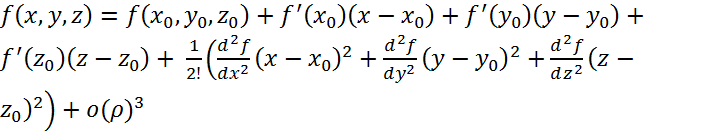
Где формула 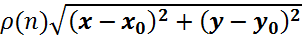приращения

Третья частная производная (f’’’) для 2х переменных:

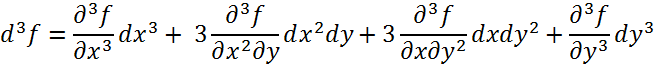
Где: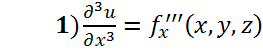

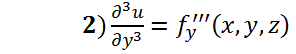
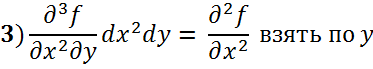
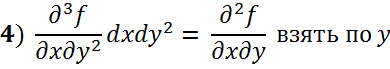
Вторая частная производная (f’’) для 2х переменных:

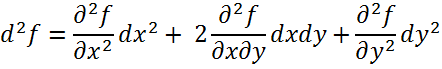
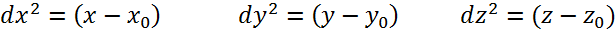
Эквивалентность Б.М и Б.Б.

Чтобы сравнить две бесконечно малые величины, нужно найти предел их отношений. И по таблице эквивалентности.

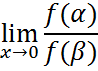
Производные первого порядка для неявно заданной функции:

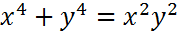
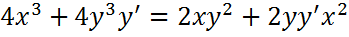
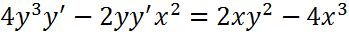
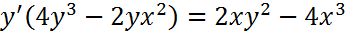
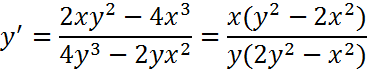
Остаточный член форма Пеано

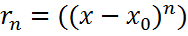где M( 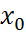). Для формулы Тейлора

Непрерывность и диф-сть ФНП

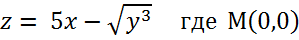
Непрерывность:

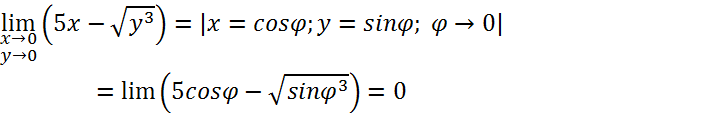
Диф-ть: (зададим приращение)

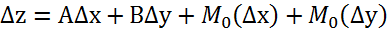
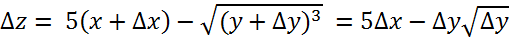
Вычисление приближённо

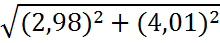
Вычислим приближённо с помощью дифференциала

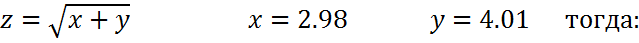
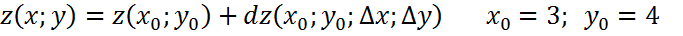
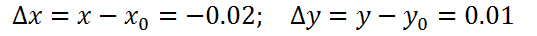
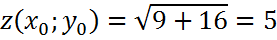
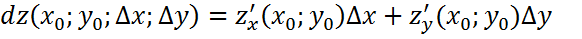
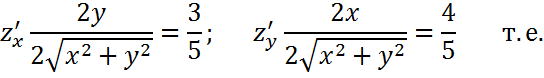
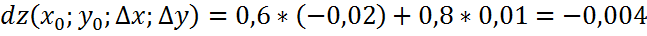
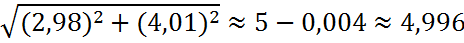
Производные высших порядков заданных параметрически

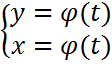
То производные 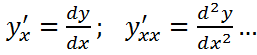последовательно могут быть вычислены по формулам:

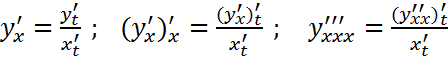и д.т.

Экстремумы трех переменных

1. Находим первые производные

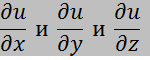
2. Составляем систему уравнения

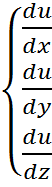Выделяем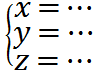

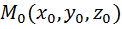
Подставляем х и у в систему находим соответствующие точки (х₁;у₁) и (х₂;у₂) т.е. М₁(х₁;у₁) и М₂(х₂;у₂)

3. Находим все вторые частные производные