Векторное пространство. Пространства арифметических и алгебраических векторов.

Векторное пространство. Пространства арифметических и алгебраических векторов.

Вектор- элемент линейного пространства

н-мерным арифметическим вектором называется упорядоченный набор из н-вещественных чисел

Обозначается x = (x1, x2, ..., xn);

числа x1, x2, ..., xn называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:

для любых x = (x1, x2, ..., xn), y = (y1, y2, ..., yn) и любого числа α справедливо:

x + y = (x1+ y1, x2 +y2, ..., xn+ yn); αx = (αx1, αx2, ..., αxn).

Достаточно умножить на это число каждый компонент

2)сложение

суммой 2х векторов называется вектор, компоненты которого являются суммами соответствующих компонентам этих векторов

1)умножение

для того чтобы умножить ,

Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.

Вектор θ = (0, 0, ..., 0) называется нулевым вектором Rn,

а вектор −x = (−x1, −x2, ..., −xn) — противоположным вектором для вектора xвRn.

Геометрический вектор - направленный отрезок

2 направленных отрезка называется равными если

у них одинаковые длины, параллельны и соноправлены

свободный вектор — это множество равных между собой направленных отрезков

Сумма векторов:

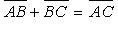(правило треугольника) (рис. 1.22);

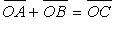(правило параллелограмма) (рис. 1.23);

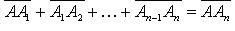(правило многоугольника);

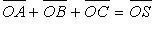(правило параллелепипеда, 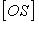- диагональ).

Разность векторов: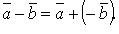

Формула вычитания векторов: 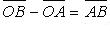(рис. 1.24).

Признак коллинеарности векторов: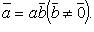

Векторное пространство

Перевод

Векторное пространство

математическое понятие, обобщающее понятие совокупности всех (свободных) Векторовобычного трёхмерного пространства.

Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление). В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям (условия А):

1) х + у = у + х (перестановочность сложения);

2)(х + у)+ z = x +(y + z) (ассоциативность сложения);

3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x;

4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,

5) 1 · х = х,

6) α(βx)=(αβ) х (ассоциативность умножения);

7) (α + β) х = αх + βх (распределительное свойство относительно числового множителя);

8) α(х + у)= αх + αу(распределительное свойство относительно векторного множителя).

Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение

α₁e₁ + α₂e₂ + … + α_ne_n (1)

называется линейной комбинацией векторов e₁, e₂,..., e_n с коэффициентами α₁, α₂,..., α_n.Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов α₁, α₂,..., α_n отличен от нуля. Векторы e₁, e₂,..., e_n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e₁, e₂,..., e_n равна нулевому вектору) векторы e₁, e₂,..., e_n называется линейно независимыми.

Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).

В. п. называется n-мepным (или имеет «размерность n»), если в нём существуют nлинейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e₁, e₂,..., e_n — базис В. п., то любой вектор хэтого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:

x = α₁e₁ + α₂e₂ +... + α_ne_n.

При этом числа α₁, α_2,..., α_n называются координатами вектора х в данном базисе.

Длина вектора

Понятие вектора

Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Направление вектора (от начала к концу) на рисунках отмечается стрелкой. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Нулевой вектор обозначается символом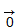

Длиной ненулевого вектора 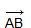называется длина отрезка AB. Длина вектора 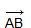(вектора 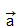) обозначается так: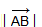 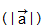. Длина нулевого вектора считается равной нулю: .
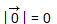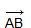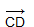Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой ил на параллельных прямых. Если два ненулевых вектора и коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы 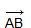и 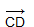называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы 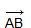и 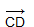называютсяпротивоположно направленными. Нулевой вектор принято считать сонаправленным с любим вектором.

Сложение матриц

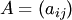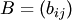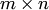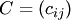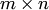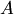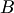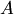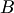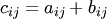
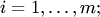
Пусть и — матрицы одинаковых размеров . Матрица тех же размеров называется суммой матриц и , если ее элементы равны сумме соответствующих элементов матриц и : 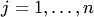. Сумма матриц обозначается .

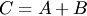Из определения следует, что складывать можно только матрицы одинаковых размеров.

Умножение матрицы на число

Произведением матрицы 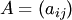на число 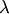называется матрица 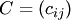тех же размеров, что и матрица 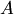, каждый элемент которой равен произведению числа 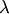на соответствующий элемент матрицы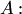

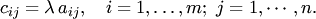
Произведение обозначается 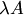или .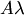

Умножить на число можно любую матрицу, при этом каждый ее элемент умножается на это число.

5. Модели планирования производства.

????????

Системы линейных уравнений

Общий вид системы

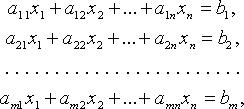
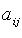, i = 1, 2, ..., m; j = 1, 2, ..., n, - коэффициенты системы; 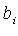- свободные члены; 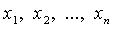- переменные;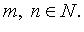

Если все 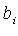= 0, система называется однородной.

Уравнение прямой в отрезках

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: 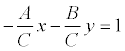или

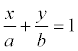, где

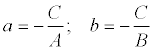
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, 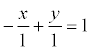, а = -1, b = 1.

Нормальное уравнение прямой

Если обе части уравнения Ах + Ву + С = 0 разделить на число 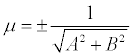, которое называется нормирующем множителем, то получим

xcosφ + ysinφ - p = 0 –

нормальное уравнение прямой.

Знак ± нормирующего множителя надо выбирать так, чтобы μ ? С < 0.

р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

уравнение этой прямой в отрезках: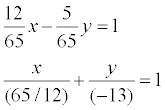

уравнение этой прямой с угловым коэффициентом: (делим на 5)

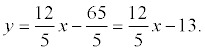
нормальное уравнение прямой:

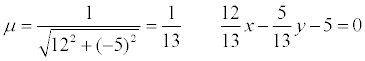; cos φ = 12/13; sin φ= -5/13; p = 5.

C ледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см ² .

Уравнение прямой имеет вид: 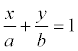, ab /2 = 8; a = 4; -4.

a = -4 не подходит по условию задачи.

Итого: 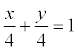или х + у – 4 = 0.

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид: 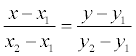>, где х ₁ = у ₁ = 0; x₂ = -2; y₂ = -3.

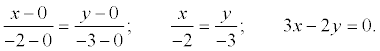
Коллинеарные прямые

Две прямые называются коллинеарными, если они параллельны или совпадают.

Получим условие коллинеарности двух прямых 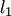и 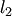, заданных общими уравнениями:

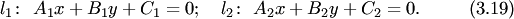
Необходимым и достаточным условием коллинеарности прямых (3.19) является условие коллинеарности их нормале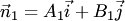й и 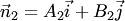. Следовательно, если прямые (3.19) коллинеарны, то 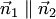, т.е. существует такое числ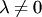о , что

и наоборот.

Прямые совпадают, если помимо этих условий справедливо 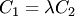. Тогда первое уравнение в (3.19) имеет вид 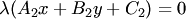, т.е. равносильно второму, поскольку .

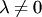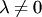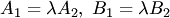Таким образом, прямые (3.19) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число , что , но 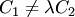. Прямые (3.19) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны:

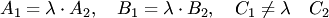
Условия параллельности или совпадения прямых (3.19) можно записать в виде

Условие коллинеарности двух прямых (3.19) можно записать в виде

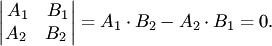
Пересекающиеся прямые

Необходимым и достаточным условием пересечения двух прямых (3.19) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

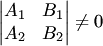или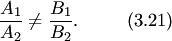

При этом условии система уравнений

имеет единственное решение 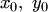, которое определяет точку 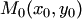пересечения прямых (3.19).

Угол между прямыми

Углом между двумя прямыми на плоскости называется угол между их направляющими векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до 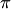. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина 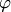угла между двумя прямыми удовлетворяет условию .

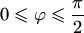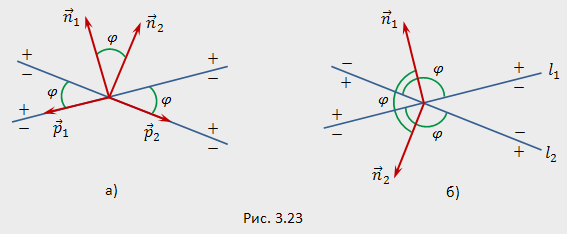
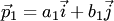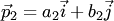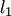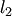Если и направляющие векторы прямых и соответственно (рис.3.23,а), то величина 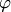угла между этими прямыми вычисляется по формуле:

Чтобы получить величину 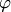острого угла между прямыми, нужно правую часть взять по абсолютной величине:

Угол 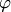между прямыми (3.19) можно вычислить как угол между их нормалям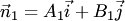и и :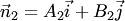

Чтобы получить величину 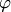острого угла между прямыми, нужно правую часть взять по абсолютной величине:

Необходимым и достаточным условием перпендикулярности прямых (3.19) является условие ортогональности их нормалей, т.е. :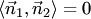

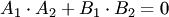
По формуле (3.22) получаем острый угол 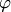между прямыми (3.19), если 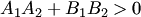(рис.3.23,а), и тупой в противном случае: 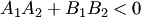(рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс 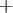или минус соответственно.

Если прямые заданы уравнениями с угловыми коэффициентами:

то угол 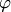между ними (один из смежных углов) находится по формуле

Если правая часть (3.23) положительна, то угол острый (рис.3.24), в противном случае - тупой. Чтобы получить острый угол , нужно правую часть (3.23) взять по абсолютной величине:

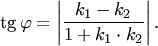
Если 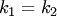(условие параллельности прямых), то 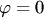. Если 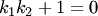(условие перпендикулярности прямых), то правая часть (3.23) не определена 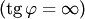. Тогда полагают, что .

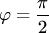Плоскостями.)

??? Плоскость в пространстве

План лекции

1. Уравнение плоскости. Полное и неполные уравнения плоскости.

2. Частные случаи уравнения плоскости.

3. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

4. Взаимное расположение двух плоскостей в пространстве.

1. Уравнение плоскости. Полное и неполные уравнения плоскости.

Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида:

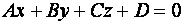(1)

Обратно, множество всех точек 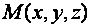,являющихся решениями произвольного уравнения (1), есть плоскость.

(1) – общее уравнение плоскости.

Пусть точка 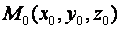лежит в плоскости (1), тогда выполняется равенство: 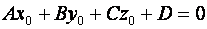(2)

Вычтем (2) из (1):

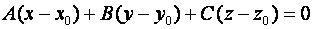
Следовательно, векторы 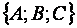и 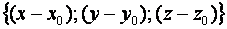ортогональны. Таким образом, вектор 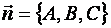является нормалью к плоскости (1) и называется нормальным вектором плоскости.

Неполные уравнения плоскости:

А) 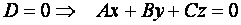- уравнение плоскости, проходящей через начало координат;

Б) 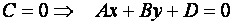- уравнение плоскости, параллельной оси ;

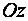В) 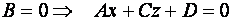- уравнение плоскости, параллельной оси ;

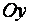Г) 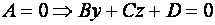- уравнение плоскости, параллельной оси ;

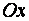Д) 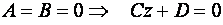- уравнение плоскости, параллельной координатной плоскости ;

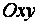Е) 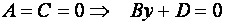- уравнение плоскости, параллельной координатной плоскости ;

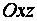Ж) 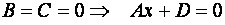- уравнение плоскости, параллельной координатной плоскости .

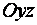2. Частные случаи уравнения плоскости.

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку 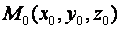и два произвольных приложенных к этой точке неколлинеарных вектора:

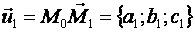и .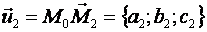

Прилагая векторы 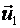и 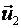к точке 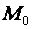, получим всевозможные закрепленные векторы вида 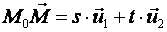, где 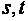- произвольные вещественные числа; концы 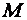этих векторов и заполняют плоскость, проходящую через точку 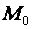и два приложенных к ней вектора .

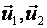В координатной форме уравнение (3) записывается так:

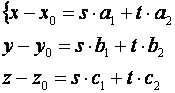(4)

(4) – параметрическое уравнение плоскости.

Уравнение (4) выражают линейную зависимость столбцов матрицы

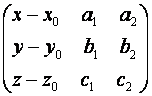
Что эквивалентно равенству:

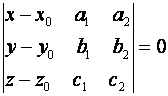(5)

Пример. Найти уравнение плоскости, проходящей через три данные точки: ; ; .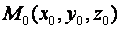

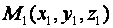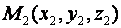Решение. Искомая плоскость содержит точку 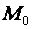и неколлинеарные векторы:

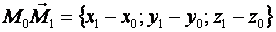и 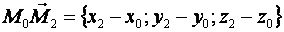, следовательно, ее уравнение можно записать в виде (5):

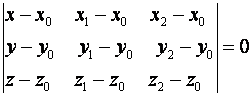
Если все коэффициенты уравнения (1) отличны от нуля, тогда его можно записать в виде:

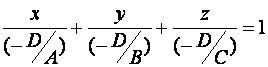
Или

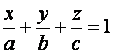(6)

Где ; ; .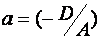

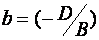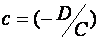(6) – уравнение плоскости в отрезках, т.к. числа 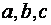- алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.

3. Нормальное уравнение плоскости. Расстояние от точки до плоскости.

Пусть дана плоскость 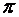. Проведем через начало координат прямую 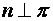, будем называть эту прямую нормалью; точка 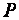- пересечение плоскости 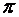и нормали 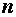. Обозначим через 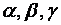углы, которые составляет вектор 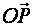с осями координат; 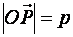. Выведем уравнение плоскости 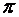, считая известными 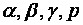. Для этого возьмем на плоскости 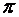произвольную точку 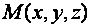, тогда 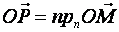, отсяда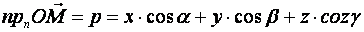

Или

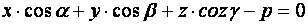(7)

(7) – нормальное уравнение плоскости.

Теорема. Расстояние 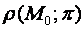от точки 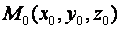до плоскости 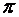вычисляется по формуле:

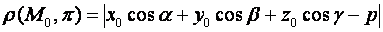
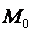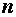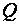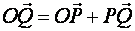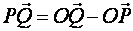Доказательство. Спроектируем точку на нормаль ; - ее проекция, тогда или , но 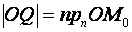; 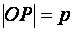, следовательно,

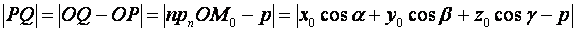
Теорема доказана.

Если плотность задана общим уравнением (1), то расстояние от точки 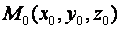до этой плоскости находится по формуле:

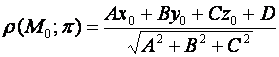
4. Взаимное расположение двух плоскостей в пространстве.

Пусть в пространстве даны две плоскост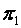и и :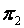

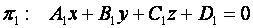
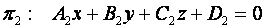
Соответствующие им векторы нормали имеют вид

,

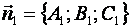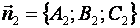
Плоскости в пространстве могут быть параллельны, совпадать, перпендикулярны и, наконец, пересекаться под произвольным углом.

Рассмотрим эти случаи.

А) Плоскост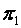и и 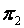параллельны, следовательно, 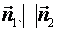, т.е. .

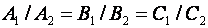Б) Плоскост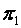и и 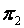совпадают, следовательно, уравнения, их описывающие, эквивалентны, т.е. .

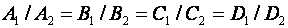В) Плоскости пересекаются под прямым углом, тогда и 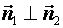, т.е. .

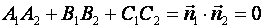Г) Плоскости пересекаются под произвольным углом; найдем этот угол. За угол между плоскостями принимается угол 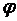между любыми двумя перпендикулярными к ним векторами, следовательно, это будет угол между нормалям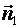и и 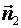, а его можно вычислить по формуле:

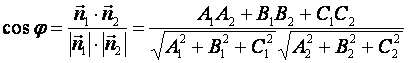
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

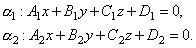
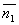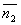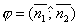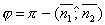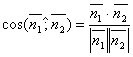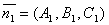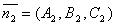Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

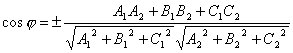Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

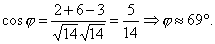
Эллипс.

Эллипсомназывается множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему

у М(х,у) координат так, чтобы ось Ох совпала с прямой F₁F₂, начало

r₁ r₂ координат – с серединой отрезка F₁F₂. Пусть длина этого

отрезка равна 2с, тогда в выбранной системе координат

F₁ O F₂ x F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и

сумма расстояний от нее до F₁ и F₂ равна 2а.

Тогда r₁ + r₂ = 2a, но ,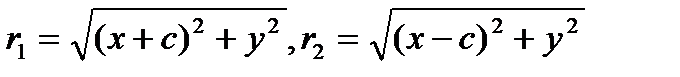

поэтому 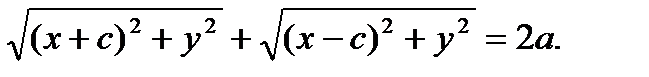Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: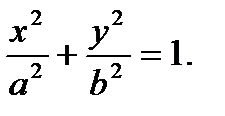

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника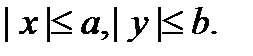

3) Эксцентриситет эллипса e < 1.

Можно доказать, что уравнение (11.7) равносильно исходному уравнению.

Оно называется каноническим уравнением эллипса. Эллипс- кривая второго порядка.

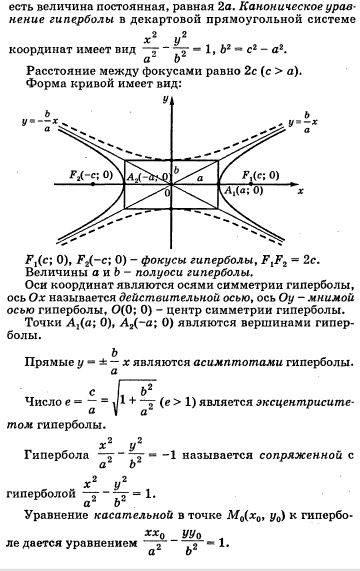
Гипербола.

Гиперболойназывается множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

|r₁ - r₂| = 2a, откуда 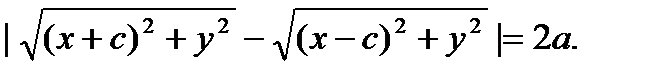Если обозначить b² = c² - a², отсюда можно получить

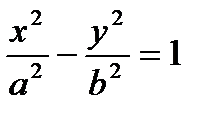- каноническое уравнение гиперболы

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениям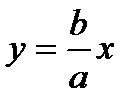и

и .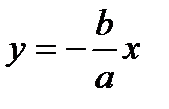

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

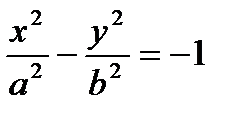, (11.3`)

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Парабола.

Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

у Для вывода уравнения параболы выберем декартову

систему координат так, чтобы ее началом была середина

d M(x,y) перпендикуляра FD, опущенного из фокуса на директри-

r су, а координатные оси располагались параллельно и

перпендикулярно директрисе. Пусть длина отрезка FD

D O F x равна р. Тогда из равенства r = d следует, что

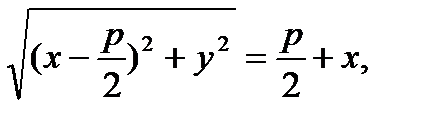поскольку

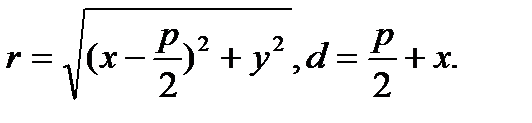Алгебраическими преобразованиями это уравнение можно привести к виду: y² = 2px

называемому каноническим уравнением параболы. Величина р называется параметромпараболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e<1), гиперболу (при e>1) или параболу (при е=1).

Квадратичные формы

Определение квадратичной формы

Квадратичная форма переменных 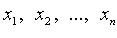- функция

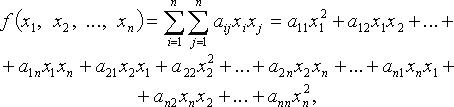
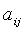- коэффициенты квадратичной формы. Без ограничения общности считают 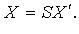тогда

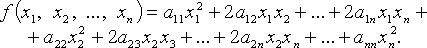
Если переменные принимают действительные значения и квадратичная форма называется действительной.

Матричная запись квадратичной формы

Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если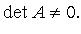

Главные миноры матрицы A называются главными минорами квадратичной формы.

В пространстве 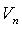квадратичную форму можно записать в виде 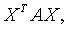где X - координатный столбец вектора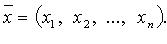

В пространстве 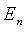квадаратичную форму можно представить в виде 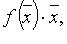где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

Векторное пространство. Пространства арифметических и алгебраических векторов.

Вектор- элемент линейного пространства

н-мерным арифметическим вектором называется упорядоченный набор из