Метод разложения на множители
Пример 1. Решите уравнение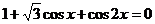 
.
Решение
Преобразуем уравнение. Применим формулу:
.
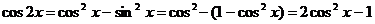Получим уравнение: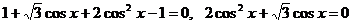 
.
Это уравнение решим разложением на множители: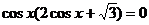 
.
Получим совокупность уравнений:
.
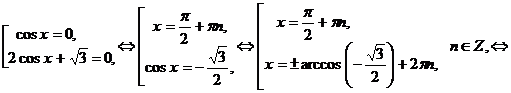
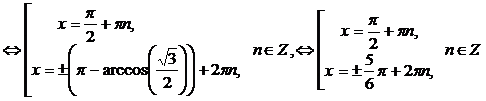Ответ: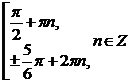 
.
Пример 2. Решите уравнение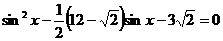 
Решение
Преобразуем уравнение: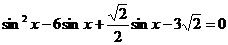 
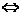
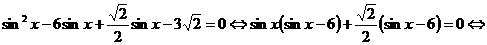
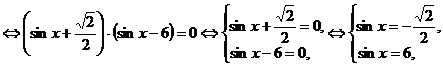
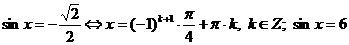- решений не имеет.
Ответ: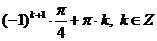 
.
Пример 3. Решите уравнение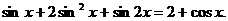 
Решение
Преобразуем уравнение. Применим формулы:
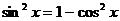и 
.
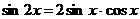Получим уравнение: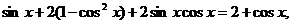 
.
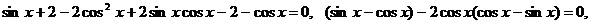
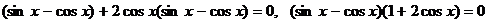Получим совокупность двух уравнений:
(1) 
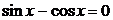и (2)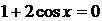 
.
Уравнение (1) 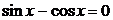является однородным. В нем 
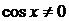. В самом деле, если допустить противное, т. е., что 
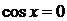, тогда, подставив его в уравнение (1), найдем, что и 
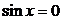, что невозможно при одних и тех же значениях аргумента (в частности, не будет выполняться основное тригонометрическое тождество 
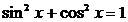). Итак, .
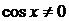Разделим обе части уравнения (1) на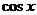 
, получим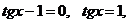 
.
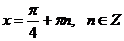Решим второе уравнение: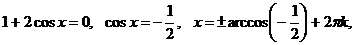 
.
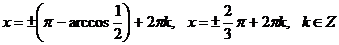Ответ: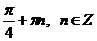 
, 
.
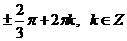Пример 4. Решите уравнение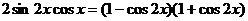 
.
Решение
Преобразуем уравнение.
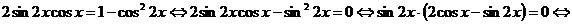
Уравнение примет вид:
.
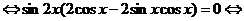
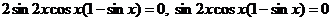Полученное уравнение равносильно совокупности уравнений:
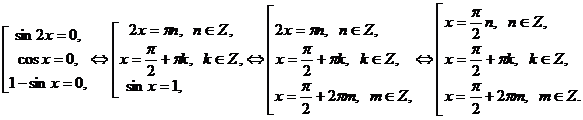
Объединим полученные решения, если это возможно. Попробуем выработать общие принципы для объединения нескольких решений в одно.
Объединим два последних решения в одно: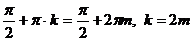 
- это значит, что при четных значениях k из множества корней 
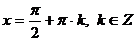получаются корни 
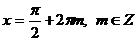, значит, 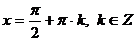являются общими решениями двух последних решений.
Далее, найдем общие решения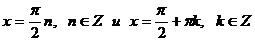 
.
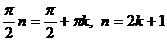, т. е. при нечетных значениях n из первого множества корней 
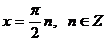получаются корни 
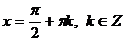, следовательно, 
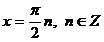- являются общими решениями трех полученных результатов.
Ответ: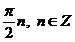 
.
Пример 5. Решите уравнение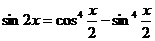 
.
Решение
Преобразуем уравнение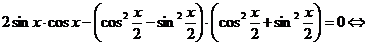 
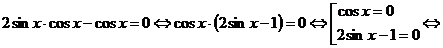
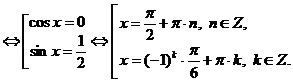
Ответ: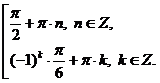 
Пример 6. Решите уравнение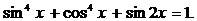 
Решение
Преобразуем уравнение, для этого прибавим к левой части уравнения и вычтем, чтобы выражение не изменилось, произведение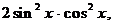 
тогда уравнение примет вид
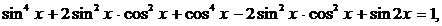
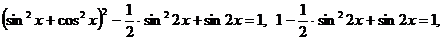
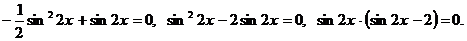
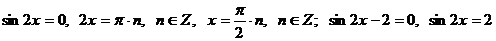- это уравнение не имеет решений, так как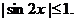 
Ответ: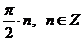 
.
Пример 7. Решите уравнение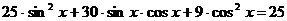 
.
Решение
I-й способ
Левая часть этого уравнения представляет собой однородное выражение относительно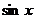 
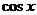и . Уравнение было бы однородным, если бы в правой части уравнения был нуль.
Для преобразования уравнения в однородное, правую часть представим в виде: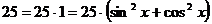 
.
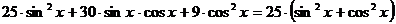, а затем все перенесем в левую часть и приведем подобные слагаемые:
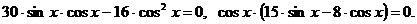
II-й способ
Преобразуем уравнение. Перенесем 25 из правой части в левую и сгруппируем с первым членом, получим: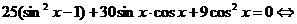 
.
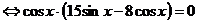Полученное уравнение равносильно совокупности двух уравнений:
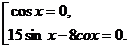
Решая первое уравнение, находим: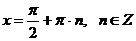 
.
Второе уравнение является однородным первой степени,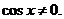 
Если допустить, что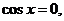 
тогда подставив это значение в уравнение, получаем: 
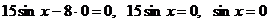. Но одновременно 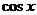и 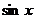не могут равняться нулю. Итак, 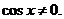Разделим на него обе части уравнения, получим:
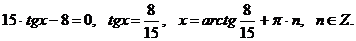
Ответ: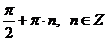 
, 
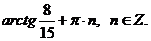
Пример 8. Решите уравнение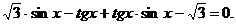 
Решение
Область допустимых значений переменной: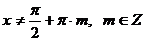 
.
Преобразуем уравнение:
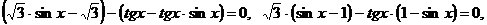
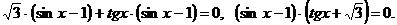
Это уравнение равносильно совокупности двух уравнений:
