Привести схему разложения многочлена на множители
Вопросы к зачету по курсу «Высшая математика»
Для студентов специальности ПОИТ
Курс 2 семестр
Записать комплексное число в алгебраической форме
I = a + jb
Записать комплексное число в тригонометрической форме
чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
z=r(cosα+isinα)
Записать комплексное число в показательной форме
z=zejφ
Как определить модуль и аргумент комплексного числа?
Модуль комплексного числа 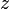 обозначается
обозначается 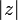 и определяется выражением
и определяется выражением 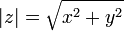
Угол 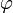 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу 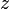 , называется аргументом числа
, называется аргументом числа 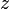 и обозначается
и обозначается 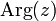 .
.
§ Из этого определения следует, что 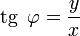 ;
; 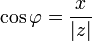 ;
; 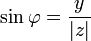 .
.
§ Для комплексного нуля значение аргумента не определено, для ненулевого числа 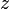 аргумент определяется с точностью до
аргумент определяется с точностью до 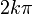 , где
, где 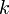 — любое целое число.
— любое целое число.
§ Главным значением аргумента называется такое значение 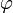 , что
, что 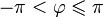 . Часто главное значение обозначается
. Часто главное значение обозначается 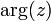 [4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:
[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: 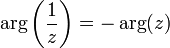 .
.
Записать формулу Муавра
Формула Муавра для комплексных чисел 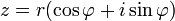 утверждает, что
утверждает, что
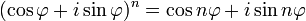
Записать формулу Эйлера
Формула Эйлера утверждает, что для любого вещественного числа 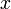 выполнено следующее равенство:
выполнено следующее равенство:
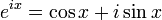 ,
,
где  — основание натурального логарифма,
— основание натурального логарифма,
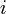 — мнимая единица.
— мнимая единица.
Записать формулу извлечения корня из комплексного числа
Если n – целое положительное число, то извлечение корня n-й степени из комплексного числа z=r(cos+isin ) осуществляется по формулам:
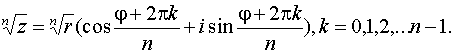
Привести схему разложения многочлена на множители
- Вынесение общего множителя за скобки.Этопреобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)
- Пример. Разложить многочлен на множители 12 y 3 – 20 y 2. Решение. Имеем: 12 y 3 – 20 y 2 = 4 y 2 · 3 y – 4 y 2 · 5 = 4 y 2 (3 y – 5). Ответ. 4 y 2(3 y – 5).
- Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
- Пример. Разложить на множители многочлен x 4 – 1. Решение. Имеем: x 4 – 1 = ( x 2 ) 2 – 1 2 = ( x 2 – 1)( x 2 + 1) = ( x 2– 1 2 )( x 2 + 1) = ( x + 1)( x – 1)( x 2 + 1). Ответ. ( x + 1)( x – 1)( x 2 + 1).
- Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.
- Пример. Разложить на множители многочлен x 3 – 3 x 2 y – 4 xy + 12 y 2. Решение. Сгруппируем слагаемые следующим образом:
x 3 – 3 x 2 y – 4 xy + 12 y 2 = ( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ). В первой группе вынесем за скобку общий множитель x 2, а во второй − 4 y . Получаем:
( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ) = x 2 ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки:
x 2 ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x 2 – 4 y ). Ответ. ( x – 3 y )( x 2 – 4 y ).
- Способ выделения полного квадрата.Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.
- Пример. Разложить на множители многочлен x 4 + 4 x 2 – 1. Решение. Имеем x4+4x2−1=x4+2
 2x2+4−4−1=(x2+2)2−5=(x2+2−
2x2+4−4−1=(x2+2)2−5=(x2+2− 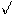 5)(x2+2−
5)(x2+2−  5)
5)
