I. Матрицы и операции над ними

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»

Экономический факультет

УТВЕРЖДАЮ

_____________________

«___» ___________2012г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ СТУДЕНТАМ ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО КУРСУ

«Линейная алгебра»

Направление подготовки (специальности) экономика

Форма обучения

заочная

Чебоксары

I. Матрицы и операции над ними

Матрицей называется прямоугольная таблица чисел

.

Обозначения: А – матрица, 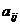- элемент матрицы, 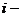номер строки, в которой стоит данный элемент, 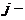номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.

Матрица называется нулевой, если все ее элементы равны 0.

Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0.

Линейные операции над матрицами

Суммой матриц А и В одинаковой размерности m 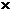n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: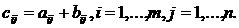

Пример 1. Найти сумму матриц 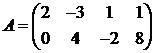и .

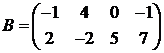Решение.

Вычислим элементы матрицы С = А + В, складывая элементы исходных матриц, стоящие на одинаковых местах:

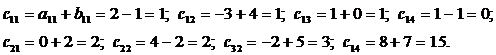
Следовательно,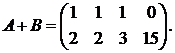

Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Пример 2. Найти матрицу 5А – 2В, если

.

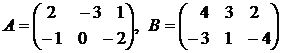Решение.

.

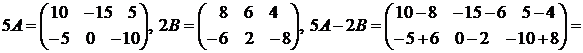
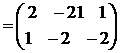Итак, 5А – 2В .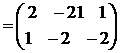

Перемножение матриц

Произведением матрицы А размерности m 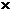p и матрицы В размерности 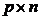называется матрица С размерности 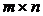, каждый элемент которой 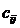определяется формулой: 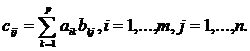Таким образом, элемент 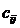представляет собой сумму произведений элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В.

Операция перемножения матриц некоммутативна, т.е. 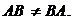Действи-тельно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей. Если существуют и АВ, и ВА, то они могут иметь разные размерности (если ).

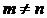Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.

Пример 3. Выяснить, можно ли умножить друг на друга матрицы

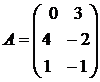и .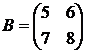

Если произведение существует, вычислить его.

Решение.

Сравним размерности матриц А и В: A[3×2], B[2×2]. Следовательно, 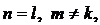поэтому произведение АВ[3×2] существует, а произведение ВА – нет.

Найдем элементы АВ:

(ab)₁₁ = 0 · 5 + 3 · 7 = 21; (ab)₁₂ = 0 · 6 + 3 · 8 = 24; (ab)₂₁ = 4 · 5 – 2 · 7 = 6;

(ab)₂₂ = 4 · 6 – 2 · 8 = 8; (ab)₃₁ = 1 · 5 – 1 · 7 = -2; (ab)₃₂ = 1 · 6 – 1 · 8 = -2.

Таким образом, 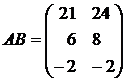, ВА не существует.

Пример 4. Найти АВ и ВА, если

.

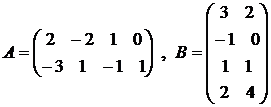Решение.

Проверим возможность перемножения матриц, определив их размерность.

A[2×4], B[4×2]. Следовательно, n = l = 4, m = k = 2, поэтому матрицы АВ и ВА существуют, причем АВ[2×2], BA[4×4].

Для вычисления элементов матрицы С = АВ элементы строк матрицы А умножаются на соответствующие элементы столбцов матрицы В:

с₁₁ = 2 · 2 + (-2)(-1) + 1 · 1 + 0 · 2 = 9

(сумма произведений элементов первой строки А на элементы первого столбца В; первый индекс вычисляемого элемента задает номер строки А, второй индекс – номер столбца В);

с₁₂ = 2 · 2 + (-2) · 0 + 1 · 1 + 0 · 4 = 5;

с₂₁ = -3 · 3 + 1 · (-1) + (-1) · 1 + 1 · 2 = -9;

с₂₂ = -3 · 2 + 1 · 0 + (-1_ · 1 + 1 · 4 = -3.

Следовательно,

.

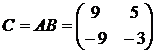При вычислении элементов матрицы D = BA элементы строк В умножаются на элементы столбцов А:

d₁₁ = 3 · 2 + 2 · (-3) = 0; d₁₂ = 3 · (-2) + 2 · 1 = -4; d₁₃ = 3 · 1 + 2 · (-1) = 1;

d₁₄ = 3 · 0 + 2 · 1 = 2; d₂₁ = -1 · 2 + 0 · (-3) = -2; d₂₂ = -1 · (-2) + 0 · 1 = 2;

d₂₃ = -1 · 1 + 0 · (-1) = -1; d₂₄ = -1 · 0 + 0 · 1 = 0; d₃₁ = 1 · 2 + 1 · (-3) = -1;

d₃₂ = 1 · (-2) + 1 · 1 = -1; d₃₃ = 1 · 1 + 1 · (-1) = 0; d₃₄ = 1 · 0 + 1 · 1 = 1;

d₄₁ = 2 · 2 + 4 · (-3) = -8; d₄₂ = 2 · (-2) + 4 · 1 = 0; d₄₃ = 2 · 1 + 4 · (-1) = -2;

d₄₄ = 2 · 0 + 4 · 1 = 4.

Таким образом,

.

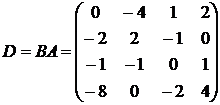Определители

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

.

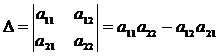При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

Пример 5.

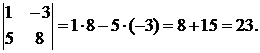
Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

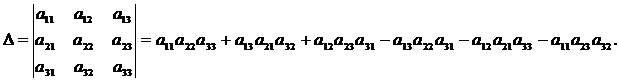
Для того чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

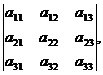
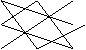образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: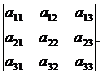

Пример 6.

Вычислить определитель

.

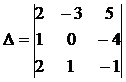Решение.

Вычислим определитель 3-го порядка, используя его определение:

Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 - 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =

= 0 + 24 + 5 – 0 + 8 – 3 = 34.

Пред тем, как перечислить основные свойства определителей, приведем определение понятия транспонирования матрицы.

Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А′, называемая транспонированнойпо отношению к матрице А, элементы которой связаны с элементами А соотношением a′_ij = a_ji .

Основные свойства определителей

1. Определитель не изменяется при транспонировании, т.е.

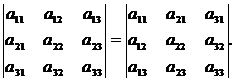
2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

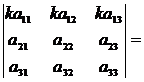
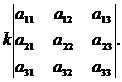
3. Определитель, имеющий нулевую строку, равен нулю:

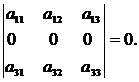
4. Определитель, имеющий две равные строки, равен нулю:

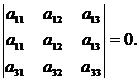
5. Определитель, две строки которого пропорциональны, равен нулю:

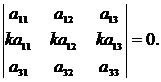
6. При перестановке двух строк определителя он умножается на –1:

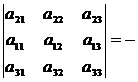
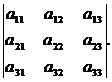
7.

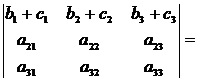
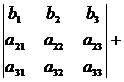
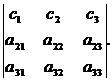
8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число:

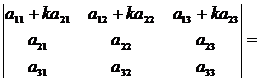
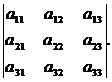
Разложение определителя по строке

Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.

Обозначение: 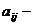выбранный элемент определителя, 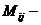его минор.

Пример 7.

Для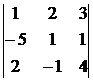

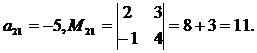
Алгебраическим дополнением 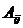элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.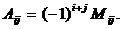

При этом справедливо следующее утверждение: определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.

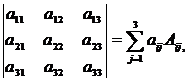где i=1,2,3.

Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.

Пример 8.

Вычислим определитель из примера 6 с помощью разложения по строке. Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (а₂₂ = 0), поскольку при этом нет необходимости находить А₂₂, так как произведение а₂₂ А₂₂ = 0. Итак,

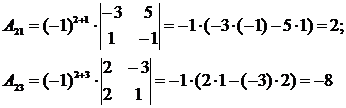
(напомним, что определитель второго порядка, входящий в алгебраическое дополнение A_ij, получается вычеркиванием из исходного определителя i-й строки и j-го столбца).

Тогда Δ = а₂₁ А₂₁ + а₂₃ А₂₃ = 1·2 + (-4)(-8) = 34.

Определители более высоких порядков

Определитель n-го порядка

есть сумма n! членов 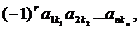каждый из которых соответствует одному из n! упорядоченных множеств 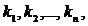полученных r попар-ными перестановками элементов из множества 1,2,…,n.

Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.

На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.

Пример 9.

Вычислить определитель 4-го порядка

.

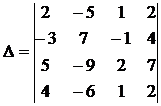Решение.

Преобразуем определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуемся свойством 8. Его особенно удобно применять, если в определителе существует элемент, равный ±1. Выберем в качестве такого элемента а₁₃ = 1 и с его помощью обратим все остальные элементы 3-го столбца в нуль. С этой целью:

а) к элементам 2-й строки прибавим соответствующие элементы 1-й строки;

б) из элементов 3-й строки вычтем элементы 1-й строки, умноженные на 2;

в) из элементов 4-й строки вычтем элементы 1-й строки

(напомним, что при этом величина определителя не изменится). Тогда

.

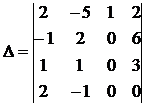Разложим полученный определитель по 3-му столбцу:

.

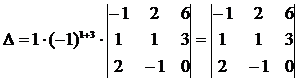Вычтем из элементов 1-й строки нового определителя удвоенные элементы 2-й строки:

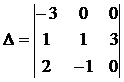
и разложим этот определитель по 1-й строке:

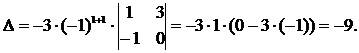
Обратная матрица

Квадратная матрица А называется вырожденной, если 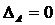, и невырожденной, если .

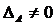Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .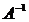

Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Тогда

,

то есть ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Пример 10.

Найти обратную матрицу для матрицы

.

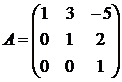Решение.

Вычислим определитель матрицы А разложением по первому столбцу:

.

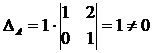Следовательно, обратная матрица для матрицы А существует.

Найдем алгебраические дополнения а элементам матрицы А:

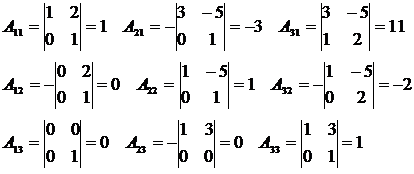
Значит,

.

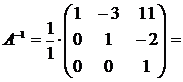
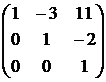Ранг матрицы

Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.

Ранг матрицы – это порядок ее наибольшего ненулевого минора (обозначения: r(A), R(A), Rang A).

Пример 11.

Определить ранг матрицы

.

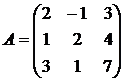Решение.

Единственным минором максимального (3-го) порядка для матрицы А является ее определитель. Если Δ_А ≠ 0, r(A) = 3; если Δ_А = 0, r(A) < 3.

Найдем Δ_А разложением по первой строке:

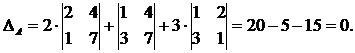
Следовательно, r(A) < 3. Поскольку матрица А содержит ненулевые элементы, r(A) > 0. Значит, r(A) = 1 или r(A) = 2. Если найдется минор 2-го порядка, не равный нулю, то r(A) = 2.

Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:

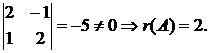
Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже 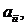равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:

1) транспонирование;

2) умножение строки на ненулевое число;

3) перестановка строк;

4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число;

5) вычеркивание нулевой строки.

Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.

Пример 12.

Определить ранг матрицы

.

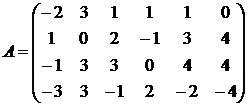Решение.

У матрицы А существуют миноры до 4-го порядка включительно, поэтому

r(A) ≤ 4. Разумеется, непосредственное вычисление всех миноров 4-го, 3-го и т.д. порядка потребовало бы слишком много времени. Поэтому, используя элементарные преобразования, приведем матрицу А к треугольному виду. Поменяем местами 1-ю и 2-ю строки, чтобы элемент а₁₁ стал равным 1:

А ~ .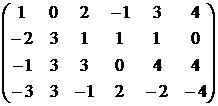

Прибавим к третьей строке первую, ко второй – удвоенную первую, к четвертой – первую, умноженную на 3. Тогда все элементы 1-го столбца, кроме а₁₁, окажутся равными нулю:

А ~ .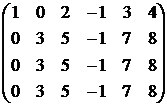

Вычтем вторую строку полученной матрицы из третьей и четвертой строк:

А ~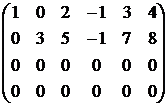

и вычеркнем нулевые строки:

А ~ .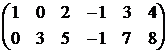

Итак, ранг матрицы А равен рангу полученной матрицы размера 2×6, т.е.

r(A) ≤ 2. Минор

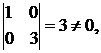
следовательно, r(A) = 2.

Метод Гаусса

Пусть в системе (1) 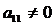(этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на 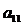и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на 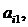где i – номер очередного уравнения. Как известно, полученная при этом новая система будет равносильна исходной. Коэффициенты при 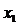во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:

.

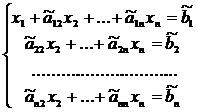Если новые коэффициенты при х₂ не все равны нулю, можнотаким же образом исключить 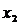из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:

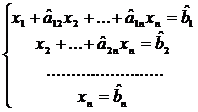. (2)

Здесь символам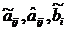и и 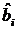обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.

Из последнего уравнения системы (2) единственным образом определяется 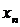, а затем последовательной подстановкой – остальные неизвестные.

Пример 13.

Решить систему методом Гаусса:

.

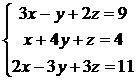Решение.

Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и

2-е уравнения, чтобы в первом уравнении коэффициент при х равнялся единице:

.

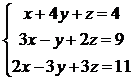Теперь исключим х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2:

.

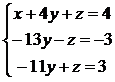Далее можно легко исключить z из третьего уравнения, если прибавить к нему второе:

.

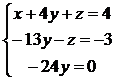Из последнего уравнения получаем, что у = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: z = 3, х = 1.

Итак, х = 1, у = 0, z = 3.

Правило Крамера

Рассмотрим линейную систему, в которой число уравнений равно числу неизвестных: 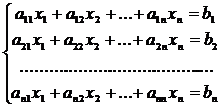(3)

Назовем главным определителем такой системы определитель 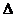, элементами которого являются коэффициенты при неизвестных:

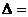
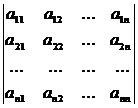, (4)

а определителем 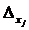- определитель, полученный из (4) заменой столбца коэффициентов при x_j на столбец свободных членов. Тогда:

1) Если 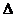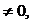система (3) имеет единственное решение, определяемое по формулам: .

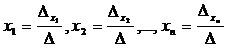2) Если 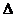= =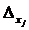0, система имеет бесконечно много решений.

3) Если 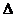= 0, а хотя бы один из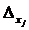 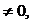система не имеет решений.

Пример 14.

Решить систему по правилу Крамера:

.

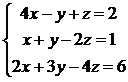Решение.

Главный определитель

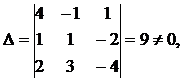
следовательно, система имеет единственное решение.

Найдем Δ_х, Δ_у и Δ_z:

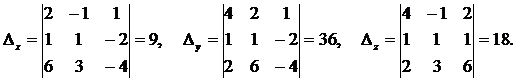
Отсюда

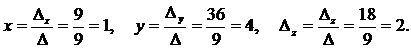
Пример 15.

Решить систему

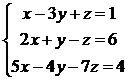
с помощью обратной матрицы.

Решение.

Составим матрицу системы:

.

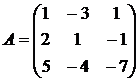Δ_А = -51 ≠ 0, следовательно, система имеет единственное решение.

Найдем матрицу А^-1:

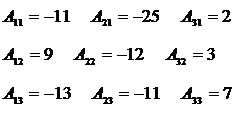
Тогда .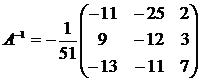

Если 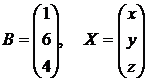, то исходная система превращается в матричное уравнение АХ = В, решение которого Х = А^-1В. Следовательно,

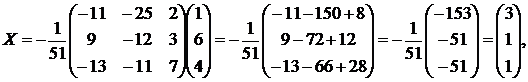
то есть х = 3, у = 1, z = 1.

Пример 16.

Найти фундаментальную систему решений однородной линейной системы

.

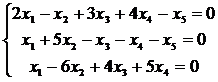Решение.

Найдем r(A):

~ ~ ~

~ .

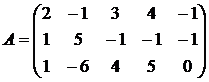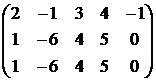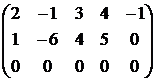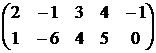Выберем в качестве базисного минора .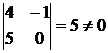

Значит, r(A) = 2. Пусть х₄, х₅ – базисные неизвестные, х₁, х₂, х₃ – свободные неизвестные. Запишем для них новую систему:

,

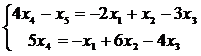откуда .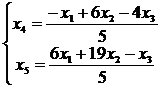

Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:

1) х₁ = 1, х₂ = х₃ = 0.

Тогда х₄ = -0,2, х₅ = 1,2, и решение можно записать в виде столбца .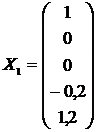

2) х₁ = 0, х₂ = 1, х₃ = 0.

При этом х₄ = 1,2, х₅ = 3,8, и следующее решение системы имеет вид .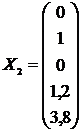

3) х₁ = х₂ = 0, х₃ = 1. Отсюда х₄ = -0,8, х₅ = -0,2, и последний столбец

.

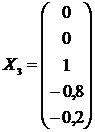Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется нормальной. Поскольку столбцы свободных неизвестных 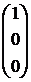, , 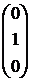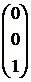линейно независимы, это гарантирует линейную независимость решений Х₁, Х₂, Х₃.

Итак, в качестве фундаментальной системы решений можно выбрать

, , .

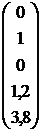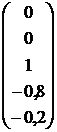При этом любое решение данной системы имеет вид: Х = с₁Х₁ + с₂Х₂ + с₃Х₃, где с₁, с₂, с₃ – произвольные постоянные. Эта формула задает общее решение системы.

Пример 17.

Найти общее решение и одно из частных решений линейной системы

.

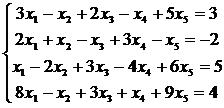Решение.

Найдем r(A) и r(A₁):

~ ~

~ ~ ~

~ .

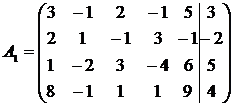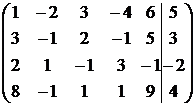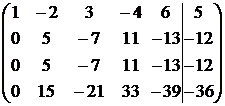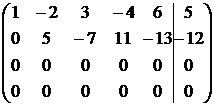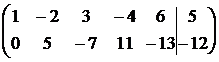Итак, r = r(A) = r(A₁) = 2, а число неизвестных п = 5. Следовательно, r < n, и система имеет бесконечно много решений (совместна, но не определена).

Число базисных неизвестных равно r, то есть двум. Выберем в качестве базисных неизвестных х₁ и х₂, коэффициенты при которых входят в базисный минор преобразованной матрицы А: .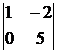

Соответственно х₃, х₄, х₅ – свободные неизвестные.

Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:

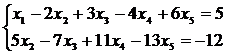
и выразим базисные неизвестные через свободные:

.

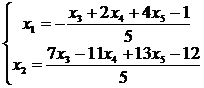Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: х₃ = х₄ = х₅ = 0. Тогда

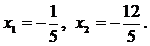
Таким образом, общее решение – ;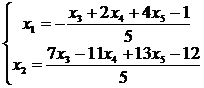

частное решение – 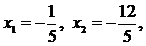х₃ = х₄ = х₅ = 0.

Другая возможность получить общее решение неоднородной системы заключается в предварительном нахождении общего решения соответствую-щей однородной системы. При этом искомое общее решение представляет собой сумму общего решения соответствующей однородной системы (6) и частного решения системы (3).

Пример 18.

Найти общее решение неоднородной линейной системы

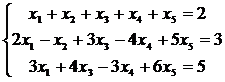
с помощью фундаментальной системы решений соответствующей однородной системы.

Решение.

Убедимся в том, что система совместна:

~ ~ ~

~ .

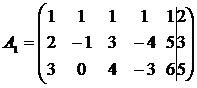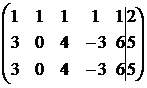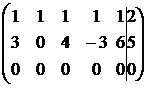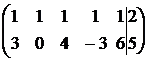Итак, r(A) = r(A₁) = 2 – система совместна.

Составим по преобразованной матрице однородную систему:

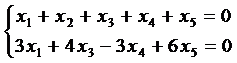
и найдем для нее фундаментальную систему решений:

,

.

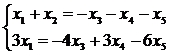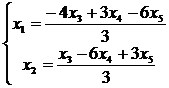Фундаментальная система решений может быть выбрана так:

, , .

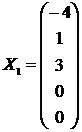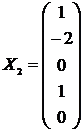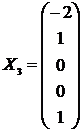Теперь найдем какое-нибудь частное решение неоднородной системы

.

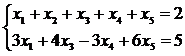Положим х₃ = х₄ = х₅ = 0, тогда 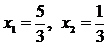. Следовательно,

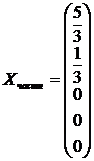, и общее решение системы имеет вид:

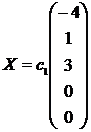
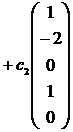
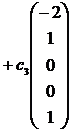
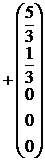, где с₁, с₂, с₃ – произвольные постоянные.

ВАРИАНТЫ ЗАДАНИЙ

Вариант задания выбирается по порядковому номеру в списке группы

Задание №1

Вычислить определитель:

1.

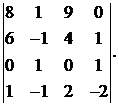
2.

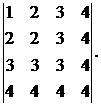
3.

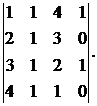
4.

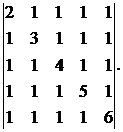
5.

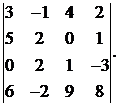
6.

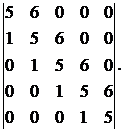
7.

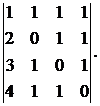
8.

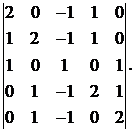
9.

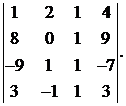
10.

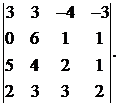
11.

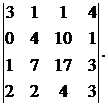
12.

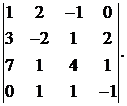
13.

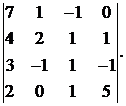
14.

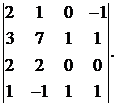
15.

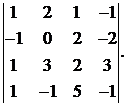
16.

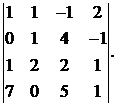
17.

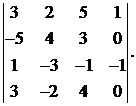
18.

19.

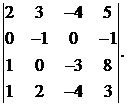
20.

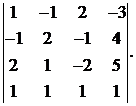
21.

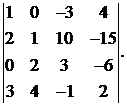
22.

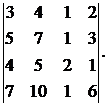
23.

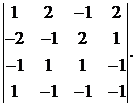
24.

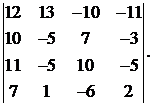
25.

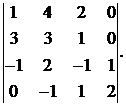
26.

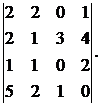
27.

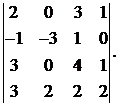
28.

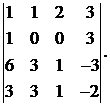
29.

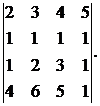
30.

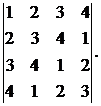
Задание №2

Для матриц A и B вычислить матричный многочлен А² – ВА + 5А.

1.

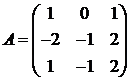
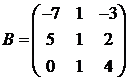
2.

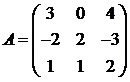
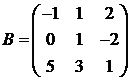
3.

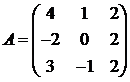
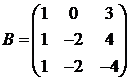
4.

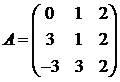
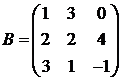
5.

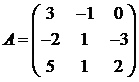
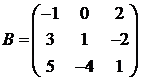
6.

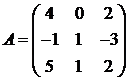
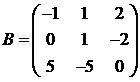
7.

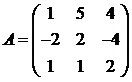
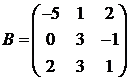
8.

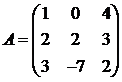
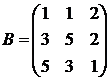
9.

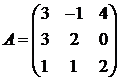
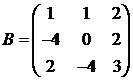
10.

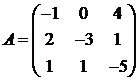
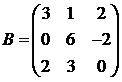
11.

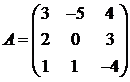
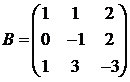
12.

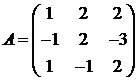
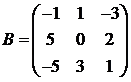
13.

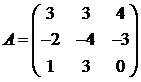
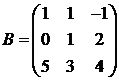
14.

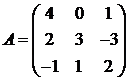
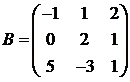
15.

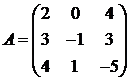
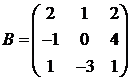
16.

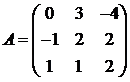
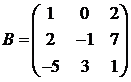
17.

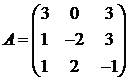
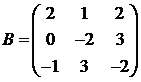
18.

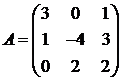
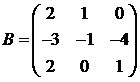
19.

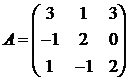
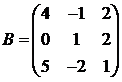
20.

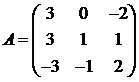
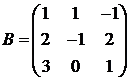
21.

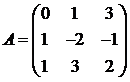
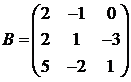
22.

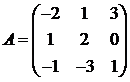
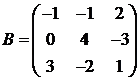
23.

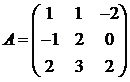
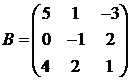
24.

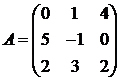
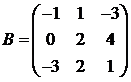
25.

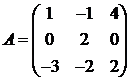
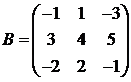
26.

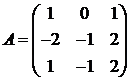
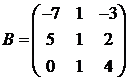
27.

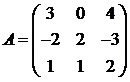
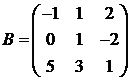
28.

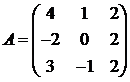
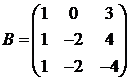
29.

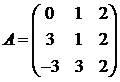
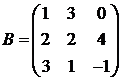
30.

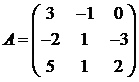
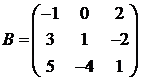
Задание №3

Вычислить обратную матрицу для матрицы:

1.

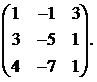
2.

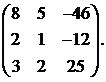
3.

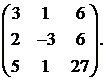
4.

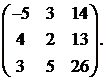
5.

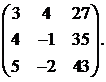
6.

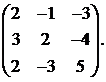
7.

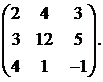
8.

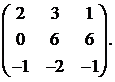
9.

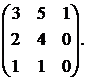
10.

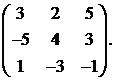
11.

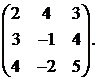
12.

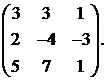
13.

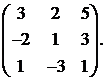
14.

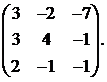
15.

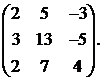
16.

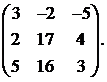
17.

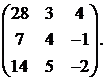
18.

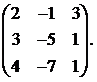
19.

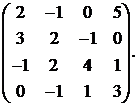
20.

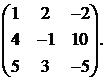
21.

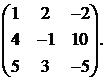
22.

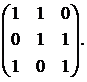
23.

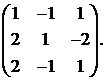
24.

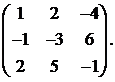
25.

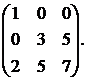
26.

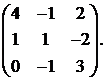
27.

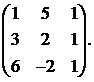
28.

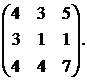
29.

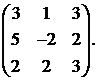
30.