Умножение матриц на действительное число.
Матрицы: определение,
Виды матриц,
Линейные операции с
Матрицами.
Матрицей размера m´ n называется таблица состоящая из m 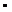 n выражений, которые расставлены в m строк и n столбцов:
n выражений, которые расставлены в m строк и n столбцов:
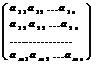

Выражения 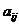
 называются элементамиматрицы.
называются элементамиматрицы.
Положение элемента в таблице характеризуется двойным индексом; первый индекс i означает номер строки, второй индекс j-номер столбца, на пересечении которых стоит элемент
(m 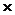 n)-матрица, все элементы которой равны нулю, называется нулевой (m
n)-матрица, все элементы которой равны нулю, называется нулевой (m 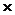 n ) - матрицей.
n ) - матрицей.
Матрица размера 1 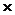 n, состоящая из одной строки, называется матрицей -строкой:
n, состоящая из одной строки, называется матрицей -строкой: 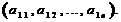
Матрица размера m 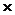 1, состоящая из одного столбца, называется матрицей- столбцом:
1, состоящая из одного столбца, называется матрицей- столбцом: 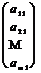 .
.
Каждая матрица, которая получается из ( m 
 n )- матрицы А вычеркиванием каких-либо строк и столбцов, называется подматрицей матрицы A.
n )- матрицы А вычеркиванием каких-либо строк и столбцов, называется подматрицей матрицы A.
Если в матрице А взаимно переставить местами строки и столбцы, то полученная матрица называется транспонированной к А и обозначается АТ; она будет иметь размер n  m :
m :
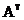 =
= 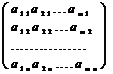 .
.
Матрица, у которой число строк равно числу столбцов ( т.е. матрица размера n 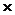 n ), называется квадратной матрицей порядка n.
n ), называется квадратной матрицей порядка n.
Элементы квадратной матрицы 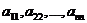
 образуют главнуюдиагональ матрицы (они стоят в таблице на диагонали квадрата, проходящей из левого верхнего угла в нижний правый); элементы
образуют главнуюдиагональ матрицы (они стоят в таблице на диагонали квадрата, проходящей из левого верхнего угла в нижний правый); элементы 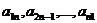 образуют побочную диагональ. Квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные равны нулю, называется единичнойи обозначается Е:
образуют побочную диагональ. Квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные равны нулю, называется единичнойи обозначается Е:
Е = 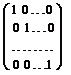 .
.
Действия над матрицами.
Равенство матрицы
Две матрицы 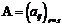 и
и 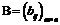 называются равными, если они имеют одинаковый размер и их соответствующие элементы ( элементы, стоящие на одних и тех же местах) равны между собой, т.е. если
называются равными, если они имеют одинаковый размер и их соответствующие элементы ( элементы, стоящие на одних и тех же местах) равны между собой, т.е. если 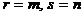 и
и 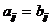
при всех i и j; тогда пишут А=В.
2) Сложение матриц одинакового размера.
Сумма двух матриц А + В одинакового размера есть матрица С того же размера с элементами 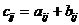 при всех i и j, т.е. сложение матриц одинакового размера происходит поэлементно.
при всех i и j, т.е. сложение матриц одинакового размера происходит поэлементно.
Умножение матриц на действительное число.
Произведение матрицы 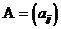 на действительное число
на действительное число 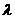 есть матрица
есть матрица 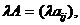 т.е. умножение матрицы на действительное число происходит поэлементно.
т.е. умножение матрицы на действительное число происходит поэлементно. 
Свойства сложения и умножения на число.
1. А + В = В + А
2. ( А + В ) + С = А + ( В + С )
3. А + Х = В 
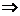 Х = В - А - разность матриц В и А
Х = В - А - разность матриц В и А
4. А + О = О + А = А
5. ( 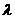
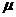 ) А =
) А = 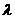 (
( 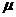 А )
А )
6. ( 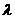 +
+ 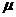 ) А =
) А = 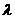 А +
А + 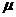 А
А
7. 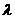 ( А + В ) =
( А + В ) = 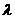 А +
А + 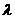 В
В
Умножение матриц
Матрицы 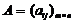 и
и 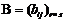 называют сцепленными в такой последовательности, если n=r , т.е. если число столбцов первой матрицы равно числу строк второй.
называют сцепленными в такой последовательности, если n=r , т.е. если число столбцов первой матрицы равно числу строк второй.
Матрицы А и В могут быть сцепленными, в то время, как матрицы В и А таковыми могут не является. Например, если матрица А размера 2 * 3, а матрица В размера 3 *4 , то матрицы А и В являются сцепленными, в то же время матрицы В и А не являютсясцепленными.
Произведение АВ двух сцепленных в такой последовательности матриц есть
матрица 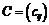 , размера ( m * s) , где
, размера ( m * s) , где 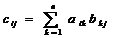 т.е. элемент, стоящий
т.е. элемент, стоящий
в i- ой строке и j- ом столбце матрицы произведения, получается в виде суммы
произведений элементов, стоящих на одинаковых местах в i-ой строке матрицы А и j-ом столбце матрицы В. Таким образом, чтобы получить 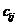 , мы должны первый элемент i-ой строки матрицы A умножить на первый элемент j-го столбца матрицы В, затем второй элемент i-ой строки матрицы А умножить на второй элемент j-го столбца матрицы В, и т.д., а затем все эти произведения сложить между собой.
, мы должны первый элемент i-ой строки матрицы A умножить на первый элемент j-го столбца матрицы В, затем второй элемент i-ой строки матрицы А умножить на второй элемент j-го столбца матрицы В, и т.д., а затем все эти произведения сложить между собой.
В данном примере произведение ВА не определено, т.к. матрицы В и А не являются сцепленными. Если даже существуют оба произведения АВ и ВА, то могут отличаться друг от друга, т.е. в общем случае АВ 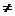 ВА.
ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными. Существует делитель нуля, т.е. существуют такие ненулевые матрицы, произведение которых есть нулевая матрица, например:
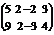
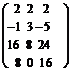 =
= 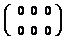
Следовательно, из того, что АВ=АС, А 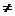 0 в общем случае не следует, что В=С.
0 в общем случае не следует, что В=С.
Если 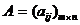 ,то домножение ее на единичную матрицу, не изменит самой матрицы :
,то домножение ее на единичную матрицу, не изменит самой матрицы : 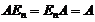
На множестве квадратных матриц одного порядка всегда выполнимы действия сложения и умножения.
3.Определитель матрицы. Вычисление определителей 2-го и 3-го порядков:
Каждой квадратной матрице А порядка n можно однозначно поставить в соответствие число D, которое называется определителем матрицы А и обозначается следующим образом:
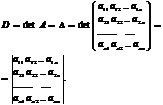 Определитель равен сумме n ! ( n! = 1
Определитель равен сумме n ! ( n! = 1  2
2  3 ... n ) слагаемых.
3 ... n ) слагаемых. 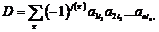 Каждое из которых представляет произведение n сомножителей, содержащее по одному элементу из каждой строки и по одному из каждого столбца. Знак
Каждое из которых представляет произведение n сомножителей, содержащее по одному элементу из каждой строки и по одному из каждого столбца. Знак 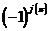 определяется числом j(
определяется числом j( 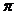 ) инверсий перестановки
) инверсий перестановки 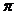 =
= 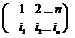
Свойства определителей.
1.Определитель не изменит своего значения, если поменять в нем местами строки и столбцы, т.е. транспонировать определитель
det A = det AT
Поэтому все свойства, сформулированные ниже для строк, верны и для столбцов.
2.Перестановка двух строк меняет знак определителя на противоположный.
3.Общий для всех элементов строки множитель можно выносить за знак определителя.
4.При сложении двух определителей, отличающихся только одной строкой, соответствующие элементы этой строки складываются, остальные остаются без изменения.
5.Прибавление к элементам i-ой строки соответствующих элементов К-ой строки, умноженных на какое-либо число, не изменяет значение определителя.
6.Определитель равен нулю, если одна строка целиком состоит из нулей или если две строки равны или пропорциональны друг другу.
Ранг матрицы
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, и называется вырожденной, если D = 0.
Говорят, что ненулевая матрица А имеет ранг rang(A)=S, если А имеет по меньшей мере одну невырожденную подматрицу порядка S, а все подматрицы А более высоких порядков вырождены.
Нахождение ранга матрицы данным образом (т.е. по определению) является достаточно трудоемким процессом. Поэтому на практике ранг матрицы вычисляют иначе, используя следующую теорему.
Теорема. Ранг матрицы не изменяется:
1) при перестановке двух строк матрицы;
2) при умножении какой-либо строки на число С 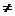 0;
0;
3) при сложении любого кратного одной строки с другой строкой;
4) при транспонировании А.
Теоремы, указанные выше для строк, справедливы и для столбцов.
Нахождение ранга матрицы А сводится к тому, чтобы с помощью данной теоремы матрицу А перевести в трапециевидную матрицу 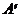 равного ранга:
равного ранга:
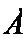

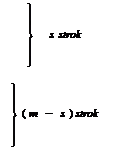
s столбцов ( n- s ) столбцов
в которой :
1) все элементы, стоящие ниже главной диагонали, равны нулю;
2) или все элементы последних( m - s) строк обращаются в нуль, или m= s
3) все элементы начала главной диагонали 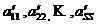 отличны от нуля.
отличны от нуля.
Тогда rang (A)= rang ( 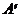 ) = s (число главных диагональных элементов, отличных от нуля). Преобразование матрицы А в трапециевидную матрицу
) = s (число главных диагональных элементов, отличных от нуля). Преобразование матрицы А в трапециевидную матрицу 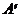 равного ранга проводится методом, который называется алгоритмом Гаусса: 1) Так как не все элементы А равны нулю, то перестановкой строк и столбцов можно добиться того, чтобы первый главный диагональный элемент был отличен от нуля
равного ранга проводится методом, который называется алгоритмом Гаусса: 1) Так как не все элементы А равны нулю, то перестановкой строк и столбцов можно добиться того, чтобы первый главный диагональный элемент был отличен от нуля 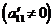 .
.
2) Сложением первой строки, умноженной на соответствующий множитель, с другими строками всегда можно добиться, чтобы все элементы, стоящие ниже 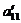 , были равны нулю.
, были равны нулю.
3) Если в строках со 2-й по последнюю имеется по крайней мере один ненулевой элемент, то он с помощью перестановок строк и столбцов может быть поставлен на второе место в главной диагонали. Тогда, складывая теперь уже вторую строку, умноженную на соответствующий множитель с нижними строками, получаем, что все элементы второго столбца. стоящие ниже второго главного диагонального элемента, равны нулю, и т.д., пока не получим трапециевидную матрицу.
Пример :
А= 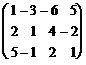 ~
~ 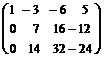 ~
~ 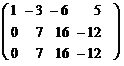 ~
~
( ко 2-й строке прибавили ( разделили 3-ю строку на 2) 1-ю, умноженную на (-2); к 3-й строке прибавили 1-ю, умноженную на (-5)
~ 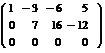 =
= 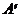 ; rang (A) = rang (
; rang (A) = rang ( 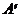 ) = 2
) = 2
( из 3-й строки вычли 2-ю).
Теорема о ранге матрицы.
Ранг матрицы равен максимальному числу линейно независимых строк (столбцов).
Строки А1 , А2 , ......... АК называются линейно независимыми, если их линейная комбинация равна нулю. 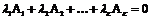 только при нулевых значениях коэффициентов
только при нулевых значениях коэффициентов 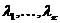 .
. 
5. Матричная форма записи системы линейных алгебраических уравнений. Виды СЛАУ:
Система уравнений вида.
(1) 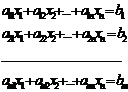
Называется системой m линейных уравнений с n неизвестными 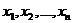 .
.
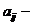 коэффициенты при неизвестных,
коэффициенты при неизвестных, 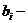 свободные члены.
свободные члены.
Если все свободные члены равны нулю, то система называется однородной.
Решением системы линейных уравнений (1) называется такая система n чисел 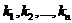 , что каждое из уравнений системы (1) превращается в тождество после замены в нем неизвестных
, что каждое из уравнений системы (1) превращается в тождество после замены в нем неизвестных 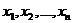 соответствующими числами
соответствующими числами 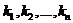 .
.
Совокупность всех решений называется множеством решений.
Две системы линейных уравнений называются эквивалентными, если они имеют одинаковые множества решений.
Если система линейных уравнений не имеет ни одного решения, то она называется несовместной, например 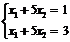
Cовместная система называется определенной, если она имеет единственное решение: 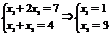
Совместная система называется неопределенной, если решений больше, чем одно: 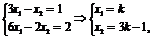 где
где 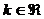
Теория системы линейных уравнений может быть наглядно описана с помощью матриц. Коэффициенты при неизвестных в системе (1) записывают в виде матрицы размера (m 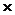 n) :
n) :
А = 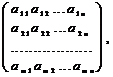 которая называется матрицей системы (1).
которая называется матрицей системы (1).
Свободные члены образуют столбец размера 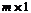
В = 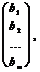 который называется столбцом свободных членов.
который называется столбцом свободных членов.
Неизвестные записываются тоже в виде столбца размера 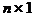
X = 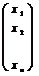 .
.
Тогда систему (1) можно записать в виде
(2) АХ = В
Такая запись называется матричной записью системы.
Убедимся, что это действительно так:
АХ = 
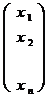 =
= 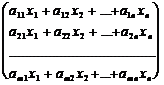
Мы получили левую часть системы (1).
Далее, из равенства матриц АХ и В следует, что соответствующие их элементы равны, и мы получаем следующую систему равенств: 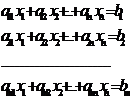
Формулы Крамера.
В определенных системах каждое из неизвестных может быть вычислено по следующей формуле:
(4) 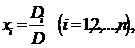
где D=detA - определитель системы, а 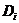 , представляет собой определитель, полученный из определителя системы D заменой i-го столбца столбцом свободных членов.
, представляет собой определитель, полученный из определителя системы D заменой i-го столбца столбцом свободных членов.
Пример 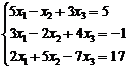 Решим систему по формулам Крамера.
Решим систему по формулам Крамера.
Определитель системы D был вычислен в предыдущем примере: 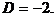
Определитель 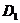 получится из определителя D, если в последнем первый столбец заменить столбцом свободных членов В:
получится из определителя D, если в последнем первый столбец заменить столбцом свободных членов В:
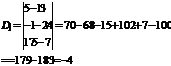
Таким образом, .
Определитель D2 получится из определителя D, если в последнем второй столбец заменить столбцом свободных членов:
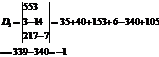
Cледовательно, 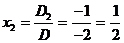
Аналогично D3 получается из D заменой третьего столбцом свободных членов:
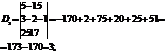
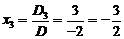
Теорема Кронекера-Капелли.
Система линейных уравнений совместнатогда и только тогда, когда ранг расширенной матрицы А* равен рангу матрицы А.
Совместная система (1) тогда и только тогда обладает единственным решением, если ранг матрицы А равен числу неизвестных;
если rang А< n  - система будет неопределенной.
- система будет неопределенной.
Определение.
Любая совокупность объектов, для которых введено соотношение равенства, а также операции сложения и умножения на число, удовлетворяющие свойствам 1-8, называется линейным векторным пространством.
Элементы такого пространства называют векторами или точками этого пространства.
Примеры линейных векторных пространств
1. Множество всех геометрических векторов.
2. Множество всех вещественных чисел. Обозначим его 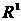 или
или 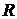 .
.
3. Множество всевозможных пар вещественных чисел. Обозначим его 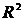 .
.
Пусть 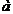 =
= 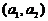 и
и 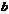 =
= 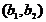 – элементы этого множества. Будем называть числа
– элементы этого множества. Будем называть числа 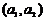 и
и 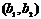 координатами векторов
координатами векторов 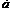 и
и  . Векторы
. Векторы 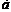 и
и 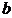 считаются равными, если равны их координаты, т.е.
считаются равными, если равны их координаты, т.е. 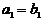 и
и 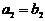
Суммой векторов 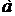 и
и 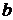 будем называть вектор
будем называть вектор 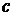 , имеющий координаты
, имеющий координаты 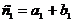 и
и 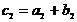 .
.
Произведением вектора 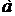 на число
на число 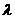 будем считать вектор
будем считать вектор 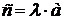 , имеющий координаты
, имеющий координаты 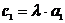 и
и 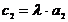 .
.
При таком введении линейных операций выполняются все свойства 1-8 и пространство 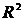 можно считать линейным векторным пространством.
можно считать линейным векторным пространством.
4. Множество всевозможных наборов из n вещественных чисел. Будем обозначать это множество 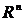 . Элементами этого множества являются наборы из
. Элементами этого множества являются наборы из 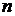 чисел.
чисел.
10.Скалярное произведение векторов и его свойства
В качестве нелинейных операций над векторами рассмотрим скалярное произведение и векторное произведение, наиболее часто встречающиеся в приложениях.
Углом между двумя векторами будем называть угол, который не превосходит p.
Угол между векторами будем обозначать 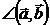
Скалярным произведением двух геометрических векторов называется число, равное произведению длин этих векторов на косинус угла между ними: 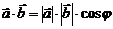
Если 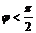 ,то
,то 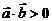 ,т.к.
,т.к. 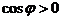 ,
,
если 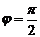 ,то
,то 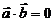 ,т.к.
,т.к. 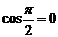 ,
,
если 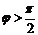 ,то
,то 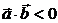 ,т.к.
,т.к. 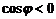 .
.
а)Ортогональной проекцией вектора 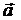 на направление, задаваемое вектором
на направление, задаваемое вектором 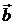 , будем называть число
, будем называть число 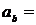
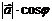
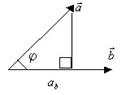
б) Аналогично число 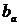 =
= 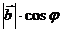 является ортогональной проекцией вектора
является ортогональной проекцией вектора 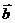 на направление
на направление 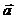 .
.
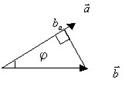
Из определения скалярного произведения следует, что
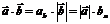
Следствие.
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны (угол между ними равен 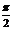 ).
).
Свойства скалярного произведения.
Коммутативность
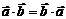
1) Ассоциативность
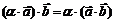
2) Дистрибутивность относительно суммы векторов
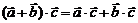
4) 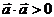 , если
, если 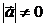 и
и 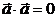 , если
, если 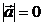
Свойства 1-4 доказываются исходя из геометрических свойств векторов.
Угол между векторами.
Зная длины векторов и их скалярное произведение можно найти угол между векторами. Действительно, т.к. 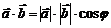 , то
, то
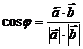
11. Векторное произведение и его свойства, вычисление через координаты
Векторным произведением 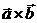 вектора
вектора 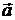 на вектор
на вектор 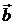 называется вектор (обозначим его
называется вектор (обозначим его 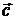 ), удовлетворяющий следующим условиям.
), удовлетворяющий следующим условиям.
1. 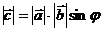 , где
, где 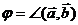 .
.
2. 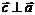 и
и 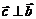 .
.
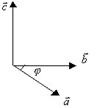
3. Направление вектора 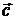 выбрано так, что со стороны вектора
выбрано так, что со стороны вектора 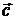 поворот от
поворот от 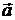 к
к 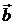 происходит против часовой стрелки.
происходит против часовой стрелки.
Свойства векторного произведения.
1. 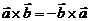
2. 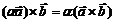 ,
, 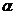 - вещественное число
- вещественное число
3. 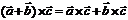
Пример
Найти площадь параллелограмма и угол 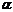 между его диагоналями, если длина сторон параллелограмма
между его диагоналями, если длина сторон параллелограмма 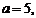
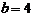 и угол между ними
и угол между ними 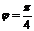 .
.
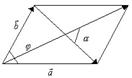
Решение.
Пусть 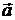 и
и 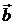 - векторы, построенные на сторонах параллелограмма. Площадь параллелограмма
- векторы, построенные на сторонах параллелограмма. Площадь параллелограмма 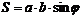 .
. 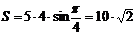 Заметим, что
Заметим, что 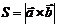 . Диагонали параллелограмма – это векторы
. Диагонали параллелограмма – это векторы 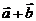 и
и 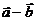 .
.
Пусть 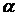 - угол между диагоналями. Тогда
- угол между диагоналями. Тогда
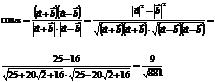
Ответ: 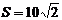 ;
; 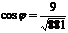 .
.
Векторное произведение векторов.
Определение: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что
- | [a,b] |=Sa,b, где Sa,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то Sa,b=0.)
- a
 [a,b]
[a,b]  b.
b. - a, b, [a,b] – правая тройка.
Свойства векторного произведения:
- [a,b] = -[b,a]
- [a,b] = θ ó a || b
- [a1+a2,b] = [a1,b]+[a2,b]
- λ·[a,b] = [λ·a,b] = [a,λ·b]
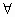 λ
λ 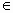 R.
R.
Утверждение 2: В декартовой системе координат (базис i, j, k), a={x1, y1, z1}, b={x2, y2, z2}
=> [a,b] = 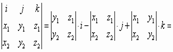
= 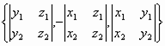
12. Смешанное произведение векторов.
Определение : Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).
Утверждение : <a,b,c>=Va,b,c, если a,b,c – правая тройка, или <a,b,c>= -Va,b,c, если a,b,c – левая тройка. Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)
Утверждение : В декартовой системе координат, если a={x1, y1, z1}, b={x2, y2, z2},
с={x3, y3, z3}, => <a,b,c>= 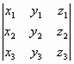 .
.
Примеры.
1. 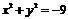 . Множество точек, удовлетворяющих этому уравнению пустое.
. Множество точек, удовлетворяющих этому уравнению пустое.
2. 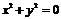 . Множество точек состоит из одной точки
. Множество точек состоит из одной точки 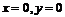 .
.
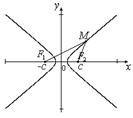
3. 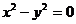 . Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии:
. Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии: 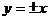 .
.
Остановимся более подробно на изучении свойств окружностей, эллипсов, гипербол и парабол.
Уравнение окружности
Окружность – это множество точек, которые находятся на одинаковом расстоянии от одной заданной точки, называемой центром окружности.
 Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку
Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку  с координатами
с координатами 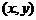 . Из определения окружности
. Из определения окружности 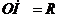 , где
, где 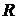 - расстояние от точек на окружности до центра. В координатной форме это условие примет вид:
- расстояние от точек на окружности до центра. В координатной форме это условие примет вид:
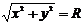 .
.
Возведя обе части уравнения в квадрат, получим каноническое уравнение окружности: 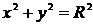 (2)
(2)
Если центр окружности расположить в точке с координатами 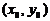 , то уравнение окружности примет вид:
, то уравнение окружности примет вид: 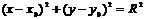 (3)
(3)
Уравнение (3) является нормальным уравнением окружности. После раскрытия скобок в этом уравнении получается общее уравнение окружности:
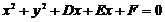 , (4)
, (4)
где 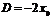 ,
, 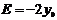 ,
,
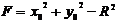 .
.
Пример 1. Найти координаты центра и радиус окружности, задаваемой уравнением: 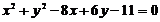 . Построить эту окружность.
. Построить эту окружность.
Решение. Сгруппируем члены, содержащие 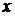 и
и 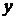 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности: 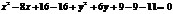 , или
, или 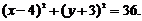
Ответ: координаты центра 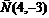 , радиус
, радиус 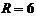 .
.
Уравнение эллипса
Эллипс – это множество точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть постоянная величина. Обозначим её 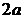 . Обозначим фокусы буквами
. Обозначим фокусы буквами 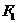 и
и 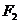 , расстояние между фокусами
, расстояние между фокусами 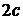 (
( 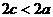 ), вершины эллипса буквами
), вершины эллипса буквами 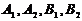 . Отрезки
. Отрезки 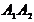 и
и 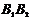 называют большой и малой осями эллипса соответственно.
называют большой и малой осями эллипса соответственно.
Введем систему координат, совместив начало координат с точкой пересечения осей 0, ось 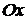 направим вдоль большой полуоси
направим вдоль большой полуоси 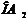 , а ось
, а ось 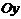 вдоль малой полуоси
вдоль малой полуоси 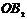 .
.
В такой системе координат уравнение эллипса примет вид:
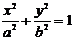 , где
, где 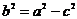 ,
, 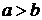 . (5)
. (5)
Уравнение (5) называют каноническим уравнением эллипса. В этом уравнении 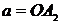 ;
; 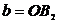 ;
; 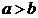 ; фокусы эллипса имеют координаты
; фокусы эллипса имеют координаты 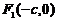 и
и 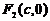 ,где
,где 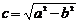 . Отношение
. Отношение 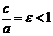 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
 Если параллельным сдвигом центр эллипса разместить в точке с координатами
Если параллельным сдвигом центр эллипса разместить в точке с координатами 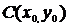 , то уравнение эллипса примет вид:
, то уравнение эллипса примет вид:
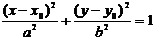 . (6)
. (6)
Пример 2. Найти координаты центра эллипса, величину большой и малой полуоси,
координаты фокусов, если эллипс задан уравнением
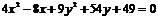 .
.
Решение. Сгруппируем члены, содержащие 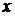 и
и 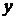 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности:
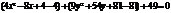 .Перегруппируем выражения в скобках, выделив полный квадрат:
.Перегруппируем выражения в скобках, выделив полный квадрат: 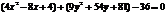 ;
; 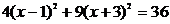 . Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса:
. Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса: 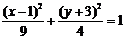 .
.
Ответ: координаты центра эллипса (1; -3), величина большой полуоси 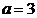 , малой полуоси
, малой полуоси
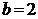 . Координаты фокусов:
. Координаты фокусов: 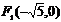 и
и 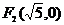 .
.
Уравнение гиперболы
Гипербола – это множество точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина.
Обозначим эту величину 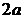 , а фокусы
, а фокусы 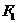 и
и 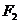 .
.
Пусть 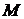 - точка на гиперболе, тогда из определения следует, что
- точка на гиперболе, тогда из определения следует, что 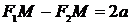 .Обозначим расстояние между фокусами
.Обозначим расстояние между фокусами 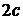 , причём
, причём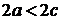 .
.
Каноническое уравнение гиперболы, симметричной относительно осей координат, примет вид
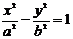 , где
, где 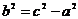 . (7)
. (7)
Обозначим вершины гиперболы буквами 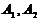 . Координаты фокусов и вершин имеют вид:
. Координаты фокусов и вершин имеют вид: 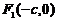 ;
; 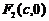 ;
; 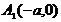 ;
; 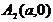 .
.
Параметр 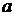 называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр
называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр 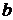 называют мнимой полуосью гиперболы, отношение
называют мнимой полуосью гиперболы, отношение 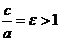 называется эксцентриситетом гиперболы. Прямые, заданные уравнениями,
называется эксцентриситетом гиперболы. Прямые, заданные уравнениями, 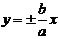 , называются асимптотами гиперболы.
, называются асимптотами гиперболы.
Если параллельным сдвигом центр гиперболы разместить в точке с координатами 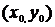 , то уравнение гиперболы примет вид:
, то уравнение гиперболы примет вид:
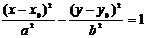 . (8)
. (8)
Пример 3. Найти координаты центра симметрии гиперболы, величину действительной и мнимой полуоси, координаты фокусов, уравнения асимптот, если гипербола задана уравнением
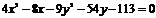 .
.
Решение. Аналогично предыдущим примерам, сгруппируем члены, содержащие 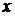 и
и 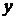 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности:
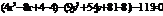 . Перегруппируем выражения в скобках, выделив полный квадрат:
. Перегруппируем выражения в скобках, выделив полный квадрат: 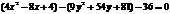 ;
; 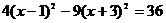 . Разделив левую и правую части выражения на 36, получим каноническое уравнение элли
. Разделив левую и правую части выражения на 36, получим каноническое уравнение элли
