Векторное произведение векторов
Определение 20. Упорядоченная тройка 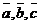 некомпланарных векторов называется положительно ориентированной (правой), если при откладывании этих векторов от одной точки кратчайший поворот от вектора
некомпланарных векторов называется положительно ориентированной (правой), если при откладывании этих векторов от одной точки кратчайший поворот от вектора  к вектору
к вектору  с конца вектора
с конца вектора 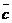 виден против часовой стрелки. В противном случае данная тройка векторов называется отрицательно ориентированной (левой).
виден против часовой стрелки. В противном случае данная тройка векторов называется отрицательно ориентированной (левой).
Определение 21. Векторным произведением упорядоченной пары неколлинеарных векторов  и
и  называется вектор
называется вектор 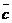 , удовлетворяющий условиям:
, удовлетворяющий условиям:
-
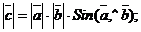
-
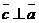 ,
, 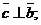
- упорядоченная тройка векторов
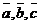 положительно ориентирована.
положительно ориентирована.
Если векторы  и
и  коллинеарны, то их векторным произведением считается нулевой вектор.
коллинеарны, то их векторным произведением считается нулевой вектор.
Векторное произведение упорядоченной пары векторов  и
и  обозначается
обозначается 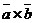 или [
или [ 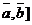 .
.
Примеры. 1. Пусть 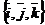 - положительно ориентированная тройка единичных взаимно перпендикулярных векторов (рис. 23). Найдём их попарные векторные произведения.
- положительно ориентированная тройка единичных взаимно перпендикулярных векторов (рис. 23). Найдём их попарные векторные произведения.
Пусть 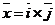 . Тогда . Тогда 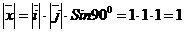 . Кроме того . Кроме того 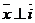 , , 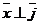 и тройка и тройка 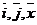 - правая. Следовательно, - правая. Следовательно, 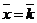 , т.е. , т.е. 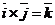 . Аналогично получим, что . Аналогично получим, что 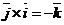 , , 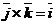 , , 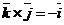 , , 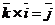 , , 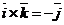 . 2. АВСD - правильный тетраэдр с ребром 1 (из точки D обход точек А, В,С виден по часовой стрелке), [DO] - его высота. Найдём . 2. АВСD - правильный тетраэдр с ребром 1 (из точки D обход точек А, В,С виден по часовой стрелке), [DO] - его высота. Найдём 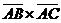 . . | 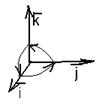 Рис. 23 Рис. 23 |
Решение. В правильном тетраэдре с ребром 1 длина высоты равна 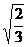 (т.е.
(т.е. 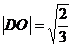 ).
).
Пусть 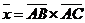 . Тогда . Тогда  (рис. 24). Кроме того, (рис. 24). Кроме того, 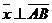 , , 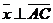 , т.е. , т.е. 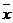 ½½ ½½ 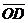 . Так как тройка векторов . Так как тройка векторов 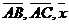 должна быть правой, а тройка должна быть правой, а тройка 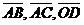 левая, то вектор левая, то вектор 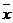 противонаправлен с вектором противонаправлен с вектором 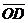 . Сравнивая длины векторов . Сравнивая длины векторов 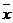 и и 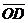 , получаем , получаем 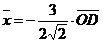 . . | 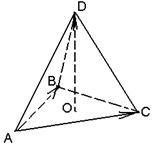 Рис. 24 Рис. 24 |
Свойства векторного произведения векторов.
10. Векторное произведение любой упорядоченной пары векторов определено и однозначно.
20. 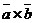 = -
= - 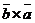 для любых векторов
для любых векторов  и
и  .
.
30. 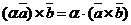 для любых векторов
для любых векторов  и
и  и любого действительного числа a .
и любого действительного числа a .
40. 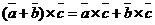 для любых векторов
для любых векторов  ,
,  и
и 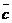 .
.
50. 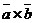 =
= 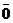 Û
Û  и
и  коллинеарны.
коллинеарны.
60. Если векторы  и и  не коллинеарны, то длина вектора, равного их векторному произведению, численно равна площади параллелограмма, построенного на этих векторах как на сторонах. Доказательство. не коллинеарны, то длина вектора, равного их векторному произведению, численно равна площади параллелограмма, построенного на этих векторах как на сторонах. Доказательство. 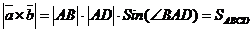 (рис. 25). 70. (Векторное произведение в координатах). (рис. 25). 70. (Векторное произведение в координатах). | 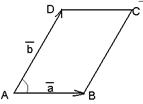 Рис. 25 Рис. 25 |
Пусть В = 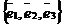 - базис,
- базис, 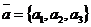 ,
, 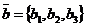 . Тогда
. Тогда
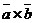 =
= 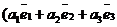 )
) 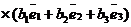 =
= 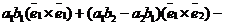
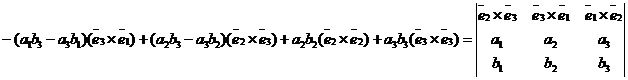
 (9)
(9)
Если базис В = 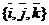 ортонормированный, то, используя пример 1, получим
ортонормированный, то, используя пример 1, получим
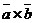 =
= 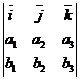 (10)
(10)
Задача 9. В ортонормированном базисе 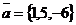 ,
, 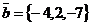 ,
, 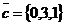 . Найдите (
. Найдите ( 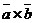 )
) 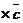 и
и 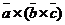 .
.
Решение. Используем формулу (10). Получим
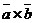 =
= 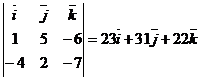 , (
, ( 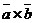 )
) 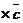 =
= 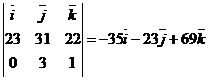 .
.
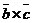 =
= 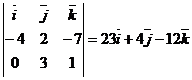 ,
, 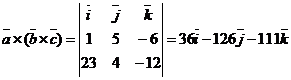 .
.
Из результатов решения этой задачи видно, что ( 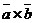 )
) 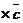 не обязано быть равно
не обязано быть равно 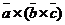 , т.е. векторное умножение векторов не подчиняется ассоциативному закону.
, т.е. векторное умножение векторов не подчиняется ассоциативному закону.
Задача 10. В параллелограмме АВСD угол ÐDАВ = 600, 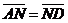 ,
, 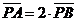 ,
, 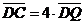 ,
, 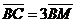 , AB = 6, AD = 4. Найдите площадь четырёхугольника MQNP и длину его высоты QE, опущенной из вершины Q.
, AB = 6, AD = 4. Найдите площадь четырёхугольника MQNP и длину его высоты QE, опущенной из вершины Q.
Решение. Разобьём четырёхугольник MQNP на два треугольника, тогда 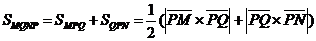 . Так как длины векторов . Так как длины векторов 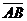 и и 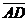 и угол между ними известны, то выберем базис и угол между ними известны, то выберем базис 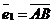 , , 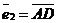 . Тогда . Тогда 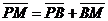 . . | 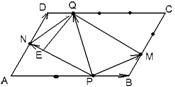 Рис. 26 Рис. 26 |
Отсюда 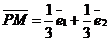 .
. 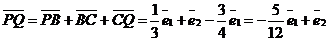 .
.
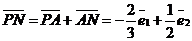 . Найдём векторные произведения.
. Найдём векторные произведения.
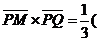
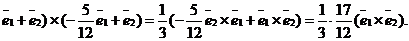 Отсюда
Отсюда
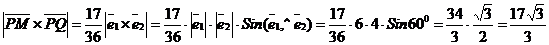 .
.
Аналогично, 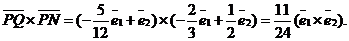
Отсюда 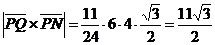 .
.
Следовательно, 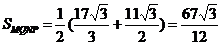 .
.
Искомая высота является высотой в треугольнике QNP. Следовательно,
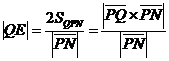 . Найдём длину вектора
. Найдём длину вектора 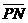 Получим
Получим 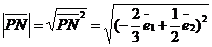 = =
= = 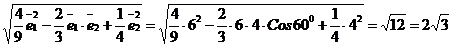 . Следовательно,
. Следовательно,
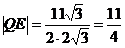 .
.
