Умножение вектора на действительное число
Определение 6. Произведением ненулевого вектора  на отличное от нуля действительное число a называется такой вектор
на отличное от нуля действительное число a называется такой вектор  (обозначение
(обозначение 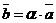 ), что
), что
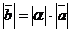 ,
,

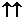
 , если a > 0,
, если a > 0,

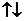
 , если a < 0.
, если a < 0.
Если 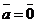 или a = 0, то вектор
или a = 0, то вектор  считается равным нулевому вектору.
считается равным нулевому вектору.
Свойства операции умножения вектора на действительное число.
10. Произведение любого вектора на любое действительное число определено и однозначно.
20. 1 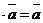 для любого вектора
для любого вектора  .
.
30. 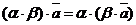 для любого вектора
для любого вектора  и любых действительных чисел a, b.
и любых действительных чисел a, b.
Доказательство. Возможны случаи.
1) a = 0, или b = 0, или  =
= 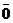 . В этом случае равенство очевидно.
. В этом случае равенство очевидно.
2) a ¹ 0, b ¹ 0 и  ¹
¹ 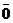 . Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
. Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
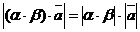 ,
,
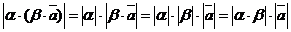 .
.
Следовательно, 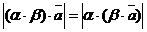 . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
. Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
а) a и b одного знака (пусть a > 0, b > 0). В этом случае a × b > 0.
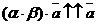 ,
,
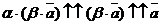 , следовательно,
, следовательно, 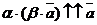 .
.
Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
б) a и b имеют разные знаки (пусть a > 0, b < 0). В этом случае a × b < 0.
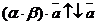 .
.
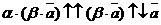 .
.
Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
40. 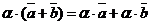 и (
и ( 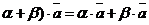 для любых векторов
для любых векторов  ,
,  и любых действительных чисел a, b. (Докажите это свойство самостоятельно).
и любых действительных чисел a, b. (Докажите это свойство самостоятельно).
Коллинеарные векторы
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Свойства коллинеарных векторов.
10. Нулевой вектор коллинеарен с любым вектором.
20. Противоположные векторы коллинеарны.
30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
40. Если вектор умножить на действительное число, то получится вектор, коллинеарный данному. Следовательно, множество коллинеарных векторов замкнуто относительно операции умножения на действительное число.
50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число.
Доказательство. Пусть векторы  и
и  коллинеарны. Если вектор
коллинеарны. Если вектор  =
= 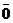 , то
, то  = 0
= 0 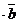 . Если
. Если  =
= 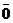 , то
, то  = 0 ×
= 0 ×  . Если
. Если  ¹
¹ 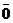 ,
,  ¹
¹ 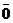 и
и 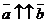 , то
, то  =
= 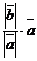 . Если
. Если 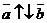 , то
, то  = -
= - 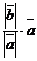 .
.
Из двух последних свойств следуют следующие два свойства.
60. (Необходимое и достаточное условие коллинеарности двух векторов)
Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них можно представить в виде произведения другого на действительное число.
70. Если вектор  не нулевой, то любой вектор, коллинеарный с вектором
не нулевой, то любой вектор, коллинеарный с вектором  , можно представить в виде
, можно представить в виде 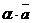 . Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
. Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
Наконец, из всех приведённых свойств можно сделать вывод, что относительно сложения векторов и умножения вектора на действительное число множество коллинеарных векторов ведёт себя так же как множество всех геометрических векторов.
Задача 2. Отрезок АВ точками С, Р, О, К, М, Т разбит на семь равных частей. Пусть
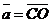 . Выразить через вектор . Выразить через вектор  векторы векторы 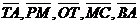 . Решение. . Решение. 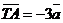 , , 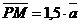 , , 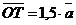 , , 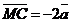 , , | 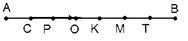 Рис. 8 Рис. 8 |
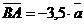 .
.
1.5. Компланарные векторы
Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости.
Свойства компланарных векторов.
10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.
30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.
Доказательство. Þ Пусть векторы 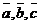 компланарны. Возможны два случая.
компланарны. Возможны два случая.
1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть  и
и  коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть
коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть 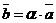 . Тогда
. Тогда 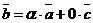 , т.е. вектор
, т.е. вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  и
и 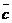 .
.
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть 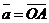 , , 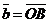 , , 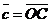 . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда 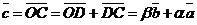 , т.е. вектор , т.е. вектор 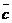 есть линейная комбинация векторов есть линейная комбинация векторов  и и  . . | 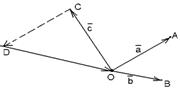 Рис. 9 Рис. 9 |
Ü Пусть 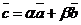 . По свойствам 10 и 20 следует, что вектор
. По свойствам 10 и 20 следует, что вектор 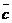 компланарен с векторами
компланарен с векторами  и
и  .
.
40. Если векторы  и
и  не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
50. Из свойств 10 и 20 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.
Задача 3. АВСD и AB1C1D1 - два произвольных параллелограмма. Докажите, что
векторы 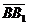 , , 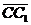 , , 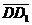 параллельны одной плоскости. Решение. Для решения задачи достаточно показать, что эти векторы компланарны. параллельны одной плоскости. Решение. Для решения задачи достаточно показать, что эти векторы компланарны. 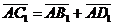 ; ; 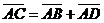 ; ; 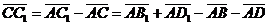 = = ( = = ( 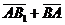 ) + ( ) + ( 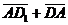 ) = ) = 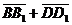 . Так как . Так как 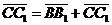 , то эти векторы компланарны . , то эти векторы компланарны . | 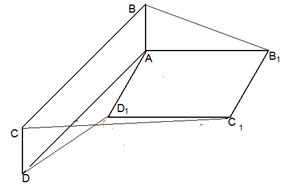 Рис. 10 Рис. 10 |
Векторные пространства
Определение 8. Множество векторов V называется векторным пространством, если в нём определены две алгебраические операции: сложение векторов и умножение вектора на действительное число, удовлетворяющие следующим требованиям:
1. Множество V замкнуто относительно обеих операций.
2. 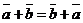 для любых векторов
для любых векторов  и
и  (коммутативный закон сложения).
(коммутативный закон сложения).
3. 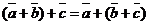 для любых векторов
для любых векторов 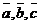 (ассоциативный закон сложения).
(ассоциативный закон сложения).
4. Существует 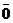 , такой, что
, такой, что 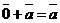 для любого вектора
для любого вектора  .
.
5. Для любого вектора  существует противоположный вектор (-
существует противоположный вектор (-  ) такой, что
) такой, что  + (-
+ (-  ) =
) = 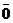 .
.
6. 1 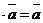 для любого вектора
для любого вектора  .
.
7. 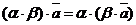 для любого вектора
для любого вектора  и любых действительных чисел a, b.
и любых действительных чисел a, b.
8. 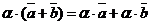 и (
и ( 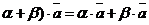 для любых векторов
для любых векторов  ,
,  и любых действительных чисел a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
и любых действительных чисел a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
Примеры векторных пространств (следуют из предыдущего материала).
1. Множество всех геометрических векторов.
2. Множество всех компланарных векторов.
3. Множество всех коллинеарных векторов.
4. Множество, состоящее из одного нулевого вектора.
