Аппроксимация выборки случайных чисел методом наименьших квадратов

Пусть требуется аппроксимировать случайную выборку значений f_i в точках x_i. Если предполагается, что вид выборки приблизительно линейный, то в качестве аппроксимационной зависимости можно выбрать линейную функцию y = ax + b.

Получим коэффициенты a и b методом наименьших квадратов.

Запишем формулу для суммы квадратов отклонений функции f_i от аппроксимационных значений y_i = ax_i + b

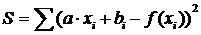(5)

Сумма квадратов отклонений S зависит от коэффициентов a и b. Необходимо найти такие а и b, при которых S минимально. Запишем условия минимума функции S(a,b) по переменным a и b:

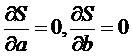(6)

Из условий (6) следуют два уравнения на коэффициенты a, b.

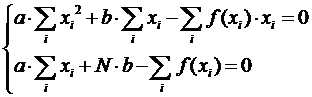(7)

Из системы (7) легко получить значения коэффициентов a и b.

Описание примера алгоритма аппроксимации выборки случайных чисел методом наименьших квадратов на естественном языке:

Задаем начальные данные для аппроксимации: границы отрезка x₀ и x_n, количество узлов координатной сетки n, шаг сетки h, массив значений координат сетки z(n) и массив значений выборки случайных чисел f(n).

Графически изображаем выборку случайных чисел f(n) на отрезке от x₀ до x_n с шагом sh.

Задаем нулевые значения вспомогательным переменным s₁=0, s₂=0 s₃=0 s₄=0 s₅=0.

Задаем цикл по i от 1 до n.

Вычисляем в цикле s₁=s₁+(x(i))²; s₂=s₂+x(i); s₃=s₃-f(i)×x(i); s₅=s₅-f(i).

Конец цикла по i.

Задаем s₄=s₂.

Вычисляем коэффициенты прямой a и b:

a=-(s₃/s₂-s₅/n)/(s₁/s₂ -s₄/n) и b=-s₃/s₂-a×s₁/s₂.

Вычисляем значение аппроксимирующей прямой в точках x₀ и x_n: f₁=a×x₀+b и f₂=a×x_n+b.

Графически изображаем аппроксимирующую прямую.

Выводим на экран значения коэффициентов прямой a и b.

Конец программы.

Пример алгоритма линейной аппроксимации выборки случайных чисел методом наименьших квадратов на естественном языке:

n=количество_узлов_сетки

Определить Массив f(n),z(n)

h=шаг_сетки

Цикл по i от 1 до n

z(i)=(i-1)*h

x=z(i)

f(i)= func1(x)

Конец Цикла

x0=начало_границы_отрезка

xn=конец_границы_отрезка

sh=шаг_аппроксимации

x1=x0

f1 = func1(x1)

Цикл по x от x0 до xn с шагом sh

x2=x+sh

f2 = func1(x2)

x1=x2

f1=f2

Конец Цикла

a=0

b=0

Вызвать м_н_к(@f,@z,n,@a,@b)

f1=a*x0+b

f2=a*xn+b

Печать a,b

Определить Процедуру м_н_к

Параметры f,x,n,a,b

s1=0

s2=0

s3=0

s4=0

s5=0

Цикл по i от 1 до n

s1=s1+x(i)^2

s2=s2+x(i)

s3=s3-f(i)*x(i)

s5=s5-f(i)

Конец Цикла

s4=s2

a=-(s3/s2-s5/n)/(s1/s2 -s4/n)

b=-s3/s2-a*s1/s2

Конец Процедуры

Определить Функцию func1

Параметры x

Возврат 2*x+0.5+0.4*Случайный()

Конец Определения Функции

Здесь запись Случайный() означает вызов стандартной функции, возвращающей псевдослучайную величину в диапазоне от 0 до 1.

Пример реализации линейной аппроксимации выборки случайных чисел методом наименьших квадратов на VFP:

SET DECIMALS TO 10

n=100

DIMENSION f(n),z(n)

h=0.1

FOR i=1 TO n

z(i)=(i-1)*h

x=z(i)

f(i)= func1(x)

ENDFOR

x0=0.05

xn=2

sh=0.05

x1=x0

f1 = func1(x1)

_screen.Cls

FOR x=x0 TO xn STEP sh

x2=x+sh

f2 = func1(x2)

_screen.Line(xe(x1),ye(f1),xe(x2),ye(f2))

x1=x2

f1=f2

ENDFOR

a=0

b=0

метод_наименьших_квадратов(@f,@z,n,@a,@b)

f1=a*x0+b

f2=a*xn+b

_screen.Line(xe(x0),ye(f1),xe(xn),ye(f2))

? a,b

procedure метод_наименьших_квадратов

PARAMETERS f,x,n,a,b

s1=0

s2=0

s3=0

s4=0

s5=0

FOR i=1 TO n

s1=s1+x(i)^2

s2=s2+x(i)

s3=s3-f(i)*x(i)

s5=s5-f(i)

ENDFOR

s4=s2

a=-(s3/s2-s5/n)/(s1/s2 -s4/n)

b=-s3/s2-a*s1/s2

RETURN

FUNCTION func1

PARAMETERS x

RETURN 2*x+0.5+0.4*RAND()

FUNCTION xe

PARAMETERS x

RETURN 50 + x*400

FUNCTION ye

PARAMETERS y

RETURN 400 - y*150

Данная реализация алгоритма для графического изображения значений выборки случайных чисел f(x) и аппроксимирующей прямойиспользует метод line(x1,y1,x2,y2) объекта _screen.

Пример реализации линейной аппроксимации выборки случайных чисел методом наименьших квадратов на VBA (для макроса MS EXCEL):

Sub MNK_Test()

Dim f(100), z(100)

Set xlSheet = Application.ActiveSheet

n = 100

h = 0.1

For i = 1 To n

z(i) = (i - 1) * h

x = z(i)

f(i) = func1(x)

Next i

x1 = 0.05

f1 = func1(x1)

sh = 0.05

xlSheet.Cells(1, 1).Value = x1

xlSheet.Cells(1, 2).Value = f1

i = 1

For x = 0.05 To 2 Step sh

i = i + 1

x1 = x + sh

f1 = func1(x1)

xlSheet.Cells(i, 1).Value = x1

xlSheet.Cells(i, 2).Value = f1

Next x

a = 0

b = 0

MNK f, z, n, a, b

x1 = 0.05

f2 = a * x1 + b

xlSheet.Cells(1, 3).Value = f2

i = 1

For x = 0.05 To 2 Step sh

i = i + 1

f2 = a * x + b

xlSheet.Cells(i, 3).Value = f2

Next x

Debug.Print "a= " & Format(a, "00.000 000 000") & " : b= " & Format(b, "00.000 000 000")

Call AddChart("C1", "C2", "C3")

End Sub

Sub MNK(fd, xd, n, a, b)

s1 = 0

s2 = 0

s3 = 0

s4 = 0

s5 = 0

For i = 1 To n

s1 = s1 + xd(i) ^ 2

s2 = s2 + xd(i)

s3 = s3 - fd(i) * xd(i)

s5 = s5 - fd(i)

Next i

s4 = s2

a = -(s3 / s2 - s5 / n) / (s1 / s2 - s4 / n)

b = -s3 / s2 - a * s1 / s2

End Sub

Function func1(x)

func1 = 2 * x + 0.5 + 0.4 * Rnd()

End Function

Sub AddChart(Col1, Col2, Col3)

ASheetName = Application.ActiveSheet.Name

Charts.Add

ActiveChart.ChartType = xlXYScatterSmooth

' ActiveChart.SetSourceData Source:=Sheets(ASheetName).Range("A1")

ActiveChart.SeriesCollection.NewSeries

ActiveChart.SeriesCollection.NewSeries

ActiveChart.SeriesCollection(1).XValues = "=" & ASheetName & "!" & Col1

ActiveChart.SeriesCollection(1).Values = "=" & ASheetName & "!" & Col2

ActiveChart.SeriesCollection(1).Name = "=""f(x)"""

ActiveChart.SeriesCollection(2).XValues = "=" & ASheetName & "!" & Col1

ActiveChart.SeriesCollection(2).Values = "=" & ASheetName & "!" & Col3

ActiveChart.SeriesCollection(2).Name = "=""g(x)"""

ActiveChart.Location Where:=xlLocationAsObject, Name:=ASheetName

ActiveChart.SeriesCollection(2).ChartType = xlXYScatterSmoothNoMarkers

ActiveChart.SeriesCollection(1).Select

ActiveChart.ChartArea.Select

End Sub

В данной реализации для графического изображения значений выборки случайных чисел f(x) и аппроксимирующей прямой (g(x))используются средства построения графиков MS’EXCEL. Значения x, f(x) и g(x) заносятся в ячейки первых трех колонок рабочего листа:

xlSheet.Cells(i, 1).Value = x1

xlSheet.Cells(i, 2).Value = f1

xlSheet.Cells(i, 3).Value = g1

и в конце программы для построения графика вызывается метод AddChart(Col1, Col2, Col3).

Результат работы программы на VBA:

Таблица значений интерполируемой и интерполяционной функций

№	x	f(x)	g(x)	№	x	f(x)	g(x)
	0,05	0,746	0,8217		1,05	2,6296	2,7175
	0,1	0,896	0,8217		1,1	2,7422	2,8173
	0,15	0,8623	0,9215		1,15	2,9327	2,917
	0,2	1,0898	1,0213		1,2	2,9513	3,0168
	0,25	1,1029	1,1211		1,25	3,0001	3,1166
	0,3	1,3515	1,2209		1,3	3,3147	3,2164
	0,35	1,4168	1,3206		1,35	3,4628	3,3161
	0,4	1,3625	1,4204		1,4	3,5176	3,4159
	0,45	1,7754	1,5202		1,45	3,731	3,5157
	0,5	1,7618	1,62		1,5	3,5328	3,6155
	0,55	1,8024	1,7197		1,55	3,6768	3,7152
	0,6	1,8562	1,8195		1,6	3,9716	3,815
	0,65	1,843	1,9193		1,65	3,9817	3,9148
	0,7	2,2136	2,0191		1,7	4,0428	4,0146
	0,75	2,1839	2,1188		1,75	4,06	4,1143
	0,8	2,4015	2,2186		1,8	4,3818	4,2141
	0,85	2,4384	2,3184		1,85	4,5715	4,3139
	0,9	2,6331	2,4182		1,9	4,5121	4,4137
	0,95	2,4075	2,5179		1,95	4,4359	4,5134
		2,5841	2,6177			4,8031	4,6132

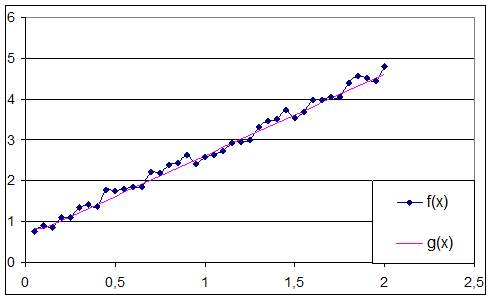
Рис 3. Графики интерполируемой (f(х)) и интерполяционной (g(x)) функций

Контрольные вопросы

1. Дать определение интерполяции функции одной переменной.

2. Что представляют собой начальные данные для интерполяции функции?

3. В чем заключается процедура интерполяции?

4. Дать определение экстраполяции функции одной переменной.

5. Что представляют собой начальные данные задачи экстраполяции функции?

6. В чем заключается процедура экстраполяции?

7. Дать определение аппроксимации функции одной переменной.

8. В чем заключается процедура аппроксимации?

9. Вывести формулы линейной интерполяции.

10. Вывести формулы линейной экстраполяции.

11. Что представляют собой начальные данные алгоритмов линейной интерполяции и экстраполяции?

12. Привести алгоритм линейной интерполяции.

13. Привести алгоритм линейной экстраполяции.

14. Как оценить погрешности при линейной интерполяции и экстраполяции?

15. Что значит «достаточно малый шаг» при линейной интерполяции и экстраполяции?

16. Привести алгоритм определения индексов соседних узлов координатной сетки.

17. Привести алгоритм задания равномерной координатной сетки.

18. Привести алгоритм задания неравномерной координатной сетки.

19. Объясните процедуру нелинейной интерполяции с использованием полинома степени n.

20. Объясните процедуру интерполяционного полинома Ньютона.

21. Объясните процедуру интерполяционного полинома Лагранжа.

22. Дать определения максимума и минимума функции двух переменных.

23. Дать определения частной производной. Что такое разностное представление частной производной? Где применяется разностное представление частной производной?

24. В чем состоит условие максимума или минимума функции двух переменных?

25. Что представляют собой начальные данные для аппроксимации методом наименьших квадратов?

26. Привести концепцию аппроксимации методом наименьших квадратов.

27. Вывести основную формулу метода наименьших квадратов.

28. Вывести основную формулу линейной аппроксимации методом наименьших квадратов.

29. Вывести основную формулу параболической аппроксимации методом наименьших квадратов.

30. Вывести основную формулу экспоненциальной аппроксимации методом наименьших квадратов

31. Привести алгоритм линейной аппроксимации методом наименьших квадратов.

32. Привести алгоритм параболической аппроксимации методом наименьших квадратов.

33. Привести алгоритм экспоненциальной аппроксимации методом наименьших квадратов

Задания

1. Написать программу на языке VFP для линейной интерполяции любой из функций, содержащейся в задании для лабораторной работы №3, на произвольном отрезке, границы которого задаются пользователем, программа выводит на экран графическое изображение интерполирующей и интерполяционной функций, а также выполняется табуляция функций с анализом ошибок интерполяции.

2. Написать программу-макрос в MS’Excel (VBA) для линейной интерполяции любой из функций, содержащейся в задании для лабораторной работы №3, на произвольном отрезке. Значения функции и ее аргумента должны считываться из текстового файла. Вывести в рабочий лист MS’Excel график интерполирующей и интерполяционной функций, а также выполнить табуляцию функций с анализом ошибок интерполяции.

3. Написать программу-макрос в MS’Word (VBA) для линейной интерполяции любой из функций, содержащейся в задании для лабораторной работы №3 на произвольном отрезке. Значения функции и ее аргумента должны считываться из документа MS’Excel. Вывести в документ MS’Excel (из макроса MS’Word) график интерполирующей и интерполяционной функций, а также выполнить табуляцию функций с анализом ошибок интерполяции.

4. Написать программу на языке VFP для линейной интерполяции любой из функций, содержащейся в задании для лабораторной работы №3, на произвольном отрезке. Значения функции и ее аргумента должны считываться из базы данных VFP. Вывести на экран графики интерполирующей и интерполяционной функций, также создать новую таблицу базы данных, содержащую данные табуляции функций с анализом ошибок интерполяции.

5. Написать программу на языке VFP для линейной интерполяции любой из функций, содержащейся в задании для лабораторной работы №3, на произвольном отрезке. Значения функции и ее аргумента должны считываться из базы данных VFP. Вывести в документ MS’Excel графики интерполирующей и интерполяционной функций, а также выполнить в MS’Excel (из программы VFP) табуляцию функций с анализом ошибок интерполяции.

6. Написать программу на языке VFP для аппроксимации методом наименьших квадратов выборки случайных чисел из заданного пользователем диапазона. Программа выводит на экран графическое изображение выборки случайных чисел и аппроксимационной функции, а также выполняется табуляция функций с анализом ошибок аппроксимации.

7. Написать программу-макрос в MS’Excel (VBA) для аппроксимации методом наименьших квадратов выборки случайных чисел из заданного пользователем диапазона. Значения функции и ее аргумента должны считываться из текстового файла. Вывести в рабочий лист MS’Excel графики выборки случайных чисел и аппроксимационной функции, а также выполнить табуляцию функций с анализом ошибок аппроксимации.

8. Написать программу-макрос в MS’Word (VBA) для аппроксимации методом наименьших квадратов выборки случайных чисел из заданного пользователем диапазона. Значения функции и ее аргумента должны считываться из документа MS’Excel. Вывести в документ MS’Excel (из макроса MS’Word) графики выборки случайных чисел и аппроксимационной функции, а также выполнить табуляцию функций с анализом ошибок аппроксимации.

9. Написать программу на языке VFP для аппроксимации методом наименьших квадратов выборки случайных чисел из заданного пользователем диапазона. Значения функции и ее аргумента должны считываться из базы данных VFP. Вывести на экран графики выборки случайных чисел и аппроксимационной функции, также создать новую таблицу базы данных, содержащую данные табуляции функций с анализом ошибок аппроксимации.

10. Написать программу на языке VFP для аппроксимации методом наименьших квадратов выборки случайных чисел из заданного пользователем диапазона. Значения функции и ее аргумента должны считываться из базы данных VFP. Вывести в документ MS’Excel графики случайных чисел и аппроксимационной функции, а также выполнить в MS’Excel (из программы VFP) табуляцию функций с анализом ошибок аппроксимации.