Приведение к общему знаменателю трех дробей с использованием разложения на множители

Рассмотрим теперь аналогичные примеры, но уже с тремя дробями.

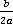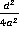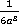Пример. 7.Привести дроби , и к общему знаменателю.

Решение.У знаменателей каждой из дробей присутствует численный коэффициент, наименьшим общим кратным для чисел 2, 4 и 6 является число 12. Буквенные множители знаменателей, в свою очередь, являются делителями выражения 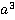. Следовательно, наименьшим общим знаменателем дробей будет 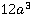. Дополнительные множители для числителей дробей находим, как и ранее: для первой дроби – 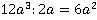, для второй – 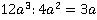, для третьей – .

; ; .

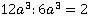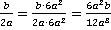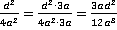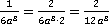Ответ. 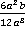, 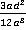и .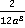

Пример 8.Привести дроб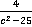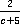и , и 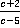к общему знаменателю.

Решение.Знаменатель первой дроби можно разложить на множители 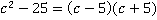. Мы видим, что он уже содержит в себе знаменатели двух других дробей в виде множителей, следовательно, для первой дроби знаменатель менять не нужно, а для двух других найдем дополнительные множители: вторая дробь – 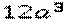, третья дробь – .

; .

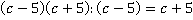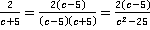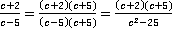Ответ. 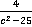, 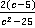и .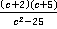

Пример 9.Привести дроб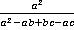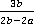и , и 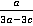к общему знаменателю.

Решение.Очевидно, что основной частью метода приведения к общему знаменателю здесь будет разложение на множители для дальнейшего поиска дополнительным множителей. Разложим первый знаменатель методом группировки множителей:

.

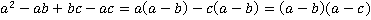Второй и третий знаменатели раскладываются с вынесением общего множителя, причем, проделаем это таким образом, чтобы получить в качестве множителей выражения соответствующие множителям первого знаменателя, чтобы проще находить затем дополнительные множители.

; .

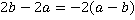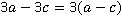Общий знаменатель дробей должен содержать все различные множители, которые мы нашли, т. е. будет равен: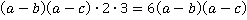

Дополнительные множители: первая дробь – 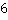, вторая дробь – ,

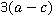третья дробь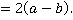

; ; .

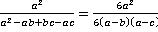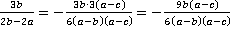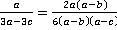Ответ. 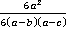, 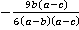и .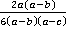

Пример на вычитание дробей с одинаковым знаменателем

Основное внимание на уроке мы уделили сложным случаям нахождения общих знаменателей у дробей. В дальнейшем это умение пригодится для проведения простейших операций с дробями, таких как сложение и вычитание. Рассмотрим один такой пример.

Пример 10.Найдите значение выражения 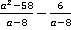при .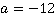

Решение.В подобных примерах подстановка числового значения в исходное выражение не является рациональной, сначала следует проделать все возможные операции в буквенном виде, т. е. упростить выражение, а уже затем подставлять числа. В данном случае необходимо вычесть дроби, они уже с одинаковыми знаменателями, поэтому поступаем, как и в случае обыкновенных дробей.

.

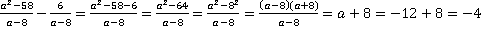Сокращение дроби на множитель 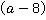мы имеем полное право проводить, т. к. значение подставляемой в дальнейшем переменной не входит в область недопустимых значений (см. урок №1). Недопустимым значением переменной в данном случае является: .

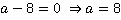Ответ. .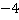

На следующих уроках мы более подробно рассмотрим технику сложения и вычитания алгебраических дробей и убедимся, что она аналогична методам работы с обыкновенными дробями.

Домашнее задание

1. Привести к общему знаменателю дроб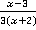и и .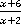

2. Привести к общему знаменателю дроб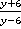и и .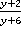

3. Привести к общему знаменателю дроб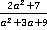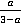и , и .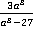

Урок 10:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (более сложные случаи).

Данный урок является логическим продолжением предыдущего, т. к. на прошлом уроке рассматривалась техника сложения и вычитания алгебраических дробей, а в рамках сегодняшнего урока будут рассмотрены более сложные случаи тех же операций над дробями. Дополнительно в рассматриваемых примерах будет делаться акцент на применение формул сокращенного умножения и на замену знака множителя на противоположный. Оказывается, что подобные процедуры могут существенно помочь при решении сложных примеров на сложение и вычитание алгебраических дробей.

Пример №1 на сложение/вычитание дробей с одинаковыми знаменателями

Вспомним изученное на прошлом уроке правило сложения и вычитания алгебраических дробей с одинаковым знаменателем:

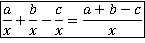
Примечательно то, что оно одинаково применимо и для простейших случаев, рассмотренных ранее, и для более сложных, которые мы сейчас разберем на примерах.

Пример 1.Сложить и вычесть указанные дроби: .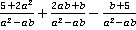

Решение.Очевидно, что указанные дроби уже с одинаковым (общим) знаменателем, и мы можем воспользоваться упомянутым ранее правилом их сложения/вычитания.

.

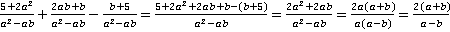Прокомментируем последовательность действий. В процессе применения правила сложения/вычитания дробей следует помнить, что такой знак, как минус перед дробью, относится ко всему числителю, и вычитать его необходимо в скобках. После приведения подобных слагаемых необходимо попытаться разложить знаменатель и числитель дроби на множители в надежде сократить на какой-то из них, что мы успешно и проделали. Затем при удачном стечении обстоятельств дробь сокращается, как в нашем случае, например, на 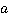. При этом стоит помнить, что любые сокращенные элементы необходимо учесть в области недопустимых значений переменных, так как они пропадают из дроби, и о них можно забыть. В нашем случае запишем, что .

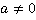Ответ. .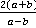

Пример №2 на сложение/вычитание дробей с одинаковыми знаменателями

Пример 2. Сложить и вычесть указанные дроби: .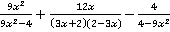

Решение.В указанном условии неочевидно, одинаковы ли знаменатели у дробей. Чтобы это проверить, разложим их на множители. При разложении на множители первого знаменателя 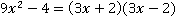видим, что он почти такой же, как и у второй дроби, противоположен только знак второго множителя. Чтобы привести знаменатели к одинаковому виду, вынесем минус из второго множителя второй дроби, и он окажется перед дробью, так как знак знаменателя и числителя относятся и ко всей дроби сразу:

.

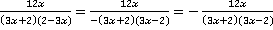Знаменатель третьей дроби тоже очень похож на знаменатель первой до разложения. Поступим с ним аналогично – вынесем минус и разложим на множители:

.

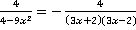Все полученные преобразования дробей подставим в исходное условие (знак перед третьей дробью получится положительным, т. к. «минус на минус дает плюс»).

.

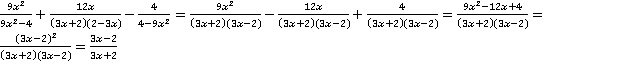В числителе воспользовались формулой квадрата разности. После сокращения учтем, что .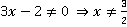

Ответ. .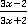

Рассмотрим теперь пример на применение умения складывать дроби с одинаковыми знаменателями в других целях.

Пример на применение сложение/вычитания дробей при доказательстве положительности выражения

Пример 3.Доказать, что выражение 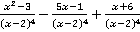принимает положительные значения при всех допустимых значениях переменной.

Решение.Поскольку необходимо исследовать выражение при всех допустимых значениях переменной, определим эти значения. По уже известному принципу, это все значения 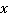, кроме 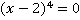. Следовательно, 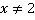. Выполним действия:

.

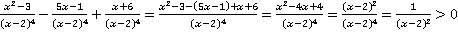После приведения подобных слагаемых мы воспользовались формулой квадрата разности 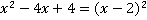, далее, т. к. 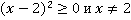, то 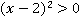. Числитель и знаменатель положительные числа, значит, и дробь положительна.

Доказано.

На следующих уроках мы поговорим уже о сложении и вычитании дробей с разными знаменателями, используя похожую на изученную нами технику.

Домашнее задание

1. Упростить выражение .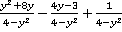

2. Упростить выражение .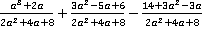

3. Упростить выражение .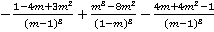

Урок 11:Сложение и вычитание алгебраических дробей с разными знаменателями.

На данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с разными знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями – одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.