N-мерные векторы, операции над ними.

В разделе векторы - основные определения мы ввели понятие вектора в двумерном пространстве (на плоскости) и в трехмерном пространстве. В этой статье мы отойдем от геометрического истолкования вектора и посмотрим на него не как на направленный отрезок, а как на упорядоченный набор чисел с присущими ему свойствами. То есть, мы рассматрим векторы с позиций алгебры, что позволит расширить понятие вектора на случай n-мерного пространства. Итак, мы дадим понятие n-мерного вектора, зададим операции над n-мерными векторами, перечислим свойства этих операций и покажем их применение при решении задач.

Определение.

Упорядоченная совокупность n действительных или комплексных чисел 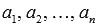называется n-мерным вектором.

Числа 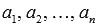называются координатами вектора.

Векторы обозначаются строчными латинскими буквами, например, a, b, c и т.п., координаты вектора указываются в скобках.

Если записать вектор a как 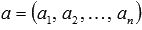, то имеем вектор-строку; если записать 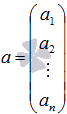, то имеем вектор-столбец. Это две формы записи одного и того же объекта - n-мерного вектора.

Обратите внимание: при обозначении n-мерных векторов стрелочка сверху над буквой (которая ставится при обозначении вектора на плоскости и в трехмерном пространстве) отсутствует.

Определение.

Вектор 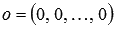, все координаты которого равны нулю, называют нулевым вектором.

Определение.

Вектор 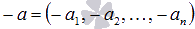называется противоположным вектору .

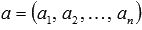Для n-мерных векторов задаются две операции: сложение векторов и умножение вектора на число.

Определение.

Суммой двух векторов 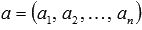и 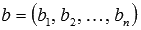называется вектор, координаты которого равны сумме соответствующих координат, то есть, .

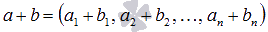Следует отметить, что складывать можно только векторы количество координат которых совпадает. Операция сложения для векторов, имеющих различное число координат, не определена.

Определение.

Произведением действительного или комплексного числа 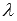и вектора 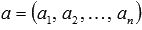называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на 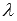, то есть, .

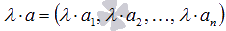Введенные таким образом операции над n-мерными векторами при n = 2 и n = 3 полностью согласуются с операциями сложения и умножения вектора на число на плоскости и в трехмерном пространстве в геометрическом смысле. Под координатами двумерного или трехмерного вектора в этом случае понимаем координаты вектора в заданной прямоугольной системе координат на плоскости или в пространстве соответственно.

Перечислим свойства операций над n-мерными векторами.

Для любых векторов 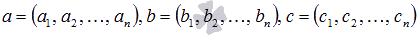и произвольных действительных или комплексных чисел 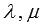справедливо:

1. свойство коммутативности сложения векторов a + b = b + a;

2. свойство ассоциативности векторов (a + b) + c = a + (b + c);

3. существует нейтральный вектор по операции сложения, им является нулевой вектор, a + 0 = a;

4. для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a + (-a) = 0;

5. Сочетательное свойство умножения .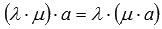

6. Первое распределительное свойство .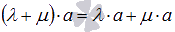

7. Второе распределительное свойство .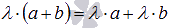

8. существует нейтральное число по операции умножения, им является единица .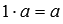

Эти свойства справедливы в силу свойств операций сложения и умножения действительных или комплексных чисел.

Операции вычитания векторов как таковой нет, так как разность векторов a и b есть сумма векторов a и -b.

Перечисленные свойства операций позволяют выполнять преобразования в выражениях содержащих векторы по тем же принципам, что и в числовых выражениях.

Билет 7