Векторы, простейшие действия над ними

Основные понятия

Понятие вектора известно из школьного курса. Наиболее часто мы будем пользоваться координатной формой записи векторов: 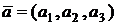. Напомним, что всегда вектор предполагается свободным, т.е. его можно без изменения длины и направления переносить в любую точку пространства. В случае координатного задания вектора его длина вычисляется по формуле:

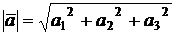. (4.1)

Направление же вектора определяется углами a, b, g, образованными вектором с положительными полуосями координат Ох, Оу, Oz, которые можно найти из формул для направляющих косинусов этих углов:

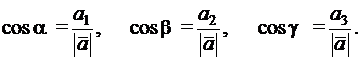(4.2)

Операции над векторами

Произведение вектора на скалярный множитель l определяется по формуле l = (lа₁, lа₂, lа₃).

Для двух векторов 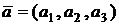, 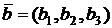их сумма и разность определяются по правилам:

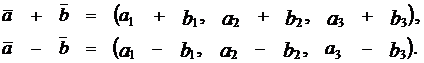
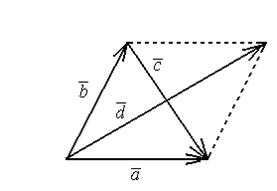
Геометрически сумма и разность векторов строится как на рисунке:

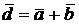Если точка О - начало координат, а М - точка с координатами (x, y, z), то вектор 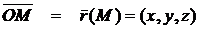называется радиусом-вектором точки М.

Вектор 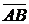с началом в точке А(x₁, y₁, z₁) и концом в точке В(x₂, y₂, z₂) в координатном виде записывается так: = .

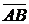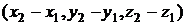Примеры.

а) В треугольнике АВС сторона АВ точками М и N разделена на три равные части: 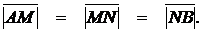Найти вектор 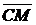, если 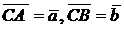. Если построить треугольник и указанные вектора, то из геометрических правил сложения и вычитания легко получаются равенства 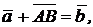т.е. 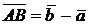. Так как 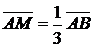, то 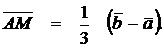Та-ким образом,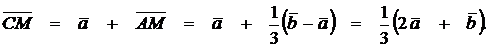

б) Найти длину вектора = (10, 15, -30) и его направляющие косинусы.

По формулам (4.1) и (4.2) определяем

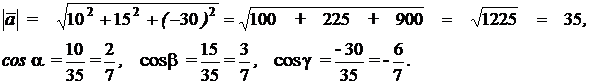
3) Найти вектор 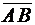, если А(2, 1, 0) и В(3, 0, 5).

Из формулы для координат вектора 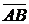имеем 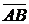= (3-2, 0-1, 5-0) =

= (1, -1, 5).

4.3. Задачи для самостоятельного решения

а) Дан треугольник АВС. На стороне ВС расположена точка М так, что 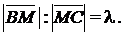Найти вектор 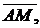если = ,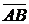

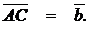
б) Найти координаты вектора 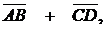где А(0, 0, 1), В(3, 2, 1), С(4, 6, 5), D(1, 6, 3).

в) Даны радиусы - векторы вершин треугольника АВС: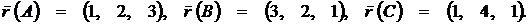

Показать, что треугольник АBC - равносторонний.

г) Вычислить длину вектора (1, 2, 1) и найти его направляющие косинусы.

д) Даны точки А(1, 2, 3) и В(3, -4, 6). Найти длину и направление вектора .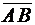

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Определение и свойства

Пусть даны два вектора и 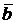.Тогда их скалярное произведение определяется из равенства 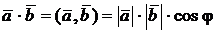, где j - угол между этими векторами.

Если векторы заданы в координатной форме 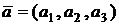, , 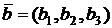то их скалярное произведение вычисляется по формуле:

.

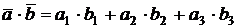Скалярное произведение векторов обладает следующими свойствами:

а) ;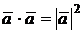

б) если ^ 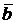(ортогональные вектора), то 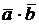= 0;

в) ;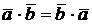

г) ;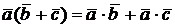

д) 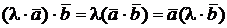, где λ- любое число.

Примеры.

а) Найти скалярное произведение векторов = (2, 1, 1) и 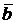= (2, -5, 1).

Из определения имеем = .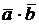

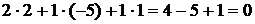б) Даны вектор = (m, 3, 4) и вектор 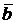= (4, m, -7). При каких значениях m вектор ортогонален вектору ?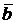

Из условий ортогональности имеем: 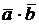= 4m + 3m -28 = 0,

7m = 28, m = 4.

в) Найти 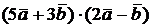, есл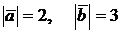и и ^ .

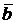Из свойств скалярного произведения имеем: ,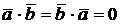

т.к. ^ 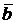, тогда

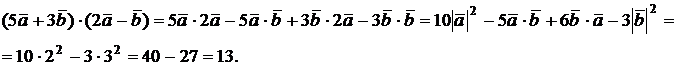
г) Определить угол между векторами = (1, 2, 3) и 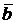= (0, 4, -2).

Так как 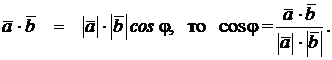Из координатного представления векторов находим 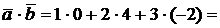0+8-6=2,

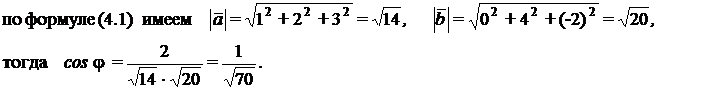
5.2. Задачи для самостоятельного решения

а) Даны векторы = (3, -2, -4), 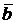= (6, -2, 3). Найти ( )( ).

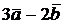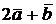б) Вычислить работу силы 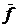= (1, 2, 1) при перемещении материальной точки из положения М₁(-1, 2, 0) в положение М₂(2, 1, 3) . Напомним, что работа вектора силы 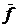равна скалярному произведению вектора 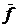на вектор перемещения _.

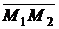в) Найти координаты вектора 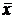, если он коллинеарен вектору

= (2, 1, 0) и его скалярное произведение на вектор равно 3, т.е.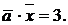

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ