Вычисление обратной матрицы с помощью алгебраических дополнений
Задана квадратная матрица 3–го порядка
| A = | æ ç ç ç è |
| ö ÷ ÷ ÷ ø | ||||||||||
Для вычисления обратной матрицы методом алгебраических дополнений
1. Вычисляем определитель матрицы A . Если det A ≠ 0 , то матрица A имеет обратную.
2. Составляем матрицу из алгебраических дополнений элементов матрицы A
| ˜A = | æ ç ç ç è |
| ö ÷ ÷ ÷ ø | . | |||||||||
3. Находим транспонированную матрицу:
| ˜AT = | æ ç ç ç è |
| ö ÷ ÷ ÷ ø | . | |||||||||
4. Разделив матрицу ˜AT на определитель, получаем искомую обратную матрицу:
A−1 =
· | æ ç ç ç è |
| ö ÷ ÷ ÷ ø | . | |||||||||||
5. Проверяем, что A · A−1 = E , и записываем ответ.
Транспонированная матрица — матрица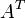 
, полученная из исходной матрицы 
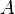заменой строк на столбцы.
Формально, транспонированная матрица для матрицы 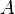размеров 
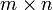— матрица 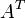размеров 
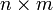, определённая как AT[i, j] = A[j, i].
Например,
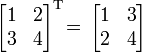и 
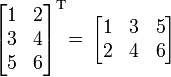
[править]Свойства транспонированных матриц
§ 
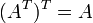
Дважды транспонированная матрица А равна исходной матрице А.
§ 
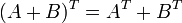
Транспонированная сумма матриц равна сумме транспонированных матриц.
§ 
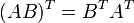
Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
§ 
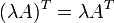
При транспонировании можно выносить скаляр.
§ 
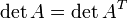
Определитель транспонированной матрицы равен определителю исходной матрицы.
Ранг матрицы
Рангом системы строк (столбцов) матрицы 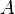с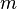 
строк и 
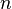столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа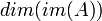 
линейного оператора, которому соответствует матрица.
Обычно ранг матрицы 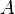обозначается 
( 
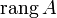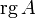) или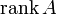 
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Определение
Пусть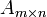 
— прямоугольная матрица.
Тогда по определению рангом матрицы 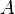является:
§ нуль, если 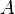— нулевая матрица;
§ число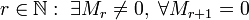 
, где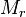 
— минор матрицы 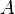порядка 
, а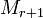 
— окаймляющий к нему минор порядка 
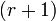, если они существуют.
Билет 8
Определение. Ранг матрицы А - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы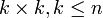 
). Обозначается 
.
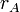Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, называются базисными строками и столбцами.
Определение. Система столбцов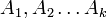 
называется линейно зависимой 
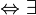числа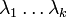 
, не все равные нулю и такие что: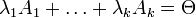 
Теорема о базисном миноре. Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.
Доказательство. Предположим противное - система длинных столбцов линейно зависима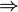 
система коротких столбцов (входящих в длинные) 
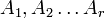линейно зависима ( 
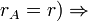по свойству определителя
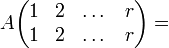БМ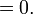 
Противоречие, т.к. БМ 
.
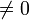Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу. Покажем, что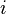 
-ый столбец линейно выражается через столбцы из БМ. 
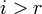(иначе он сам является столбцом из БМ). Рассмотрим минор порядка на один больше, он будет нулевой.
Фиксируем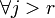 
. Раскладываем определитель по 
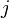-ой строке:
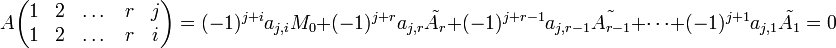так как минор порядка 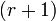- нулевой (где 
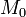- БМ 
. Выражаем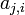 
: 
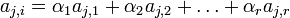Получены коэффициенты 
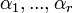. Для любого 
: 
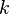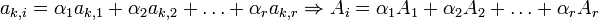(так как 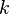- любое)
Следствие. Если все столбцы матрицы А линейно выражаются через r столбцов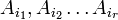 
, которые образуют линейно независимую систему, то 
.
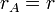Доказательство. Столбцы входящие в максимальную линейно независимую систему (в кол-ве 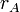штук) линейно выражаются через 
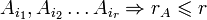. столбцы 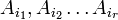(в кол-ве r штук) линейно выражаются через максимальную линейно независимую систему в кол-ве 
.
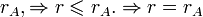Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).
Доказательство. Пусть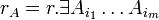 
- столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов 
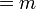(число столбцов входящих в максимальную линейно независимую систему ) 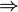по утверждению 1 (если система линейно независима (количество 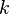) и выражается через другую (количество 
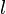) то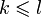 
) 
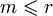. по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы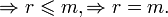 
Определение ранга матрицы
Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называетсярангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядкаr, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение
