Наибольшее/наименьшее значение функции

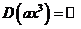, то функция не имеет наибольшего и наименьшего значения

График функции.

О. Графиком кубической функции является кривая, называемая кубическойпараболой (рис.4).

6. Свойства функции 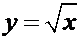и её график

Рассмотрим функцию вида: .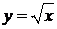

Свойства:

1. Область определения функции: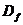

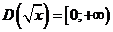(по свойствам квадратного корня) (см. § 28)

2. Множество значений функции: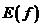

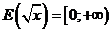(почему?)

3. Периодичность:

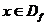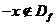Если , то , значит функция не определена в точке 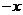, а значит, функция 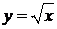не является периодической.

Чётность/нечётность

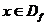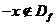Если , то , значит, функция не определена в точке 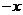, а, значит, функция не является ни четной, ни нечетной.

Точки пересечения графика с осями координат.

Точки пересечения с осью 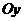: если

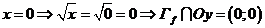
Точки пересечения с осью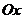

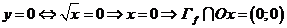
6. Промежутки знакопостоянства функции:

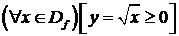
Интервалы возрастания/убывания

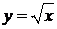возрастает на всей области определения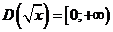

8. Наибольшее/наименьшее значение функции

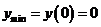
- не существует.

График функции

(рис 11).

7. Свойства функции 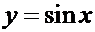и её график

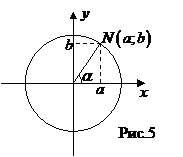Рассмотрим окружность с центром, расположенным в начале координат, и радиусом, равным единице (это так называемая тригонометрическая окружность).

Для любогодействительного числа 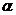можно провести радиус ON этой окружности, образующий с осью 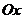угол, радианная мера которого равна числу 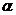(положительным считается направление поворота против хода часовой стрелки). (рис 5)

О. Число, равное ординате конца единичного радиуса, задающего угол 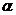, называется синусом угла 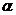и обозначается .

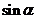Т.к. каждому значению величины угла 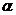на тригонометрической окружности соответствует единственная точка 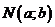, такая, что радиус ON образует угол 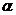с осью 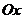, то данное определение задает функцию .

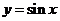Свойства:

1. Область определения функции: .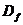

Т.к. для любого значения угла однозначно определена точка, являющаяся концом соответствующего радиуса, то область определения функции : .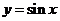

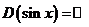2. Множество значений функции:

Теорема.

Множеством значений функции является промежуток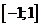

Доказательство:

Действительно, ордината всякой точки, являющейся концом радиуса тригонометрической окружности, может принимать лишь значения из отрезка .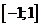

С другой стороны, для значения ординаты 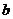из этого отрезка можно указать хотя бы одну точку на окружности, имеющую эту ординату.

Следовательно, это значение 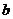будет синусом угла, образованного положительным направлением оси 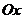и радиусом, соединяющим центр окружности и построенную точку.

3. Периодичность:

Наименьший положительный период функции 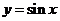равен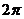

Доказательство:

Т.к. центральный угол, соответствующий полной окружности, равен 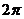, то точки, соответствующие углам 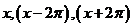изображаются на тригонометрической окружности одной и той же точкой, следовательно, синусы этих углов равны.

Это означает, что число 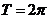является периодом рассматриваемой функции.

Докажем, что 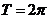- наименьший положительный период.

Рассмотрим значение функции 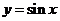, равное 1. Оно достигается только при 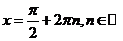. Значит, никакое число, меньшее 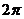, не может быть периодом. Значит, что 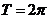- действительно наименьший положительный период функции .

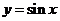Чётность/нечётность

Рассмотрим точки M и N, соответствующие на тригонометрической окружности углам 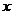и 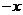. Поскольку всякая окружность симметрична себе относительно своего диаметра (диаметр тригонометрической окружности лежит на оси 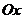), а равные по величине углы при симметрии переходят в равные углы, то точки M и N симметричны относительно оси 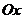, следовательно, их ординаты противоположны. Это означает, что для всех х из области определениявыполняется равенство 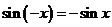, т.е. функция 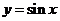является нечетной.