Описание пограммы EL12Maltus.

Программа EL12Maltusпредназначена для расчета и отображения

- функций рождаемости, смертности, мальтузианской функции,

- скорости изменения относительной численности популяции

- при заданных значениях параметров популяции,

- на заданном промежутке значений ее относительной численности,

- при заданном шаге вычислений.

Войдите в среду МАТЛАБ и с помощью меню «Файл» откройте программу.

Рассмотрите ее состав, использование команд.

В приводимых ниже строках ввода данных установлены промежуток и шаг расчетов, параметры популяции. Вы можете согласиться с введенными данными или изменить их по своему усмотрению.

Остальные строки программы в лаборатории изменять не разрешается, дома тоже лучше воздержаться от этого.

N=0:.1:5;

NChild=3; % стандарт - 3, варьируйте от 1 до 5;

Narc=.001; % стандарт - .001, варьируйте до .05-.1;

Commun=1.5; % >1, стандарт - 1.5;

QLife=1; % стандарт - 1, диапазон - от 0.5 до 1.5;

Contest=1.1; % стандарт - 1.1, диапазон - от 1 до 2.

Сохраните программу.

В рабочем окне МАТЛАБ-а

- наберите ее название EL12Maltus,

- получите графики функций рождаемости, смертности, мальтузианской функции (Рис.1).

После повторного нажатия на клавишу «Ввод» получите график скорости изменения относительной численности популяции в функции этой численности при заданных значениях параметров, то есть фазовый портрет популяции (Рис.2).

Рис. 1 Функции рождаемости, смертности, мальтузианская функция.

Рис. 2 Фазовый портрет популяции.

Оценка динамику популяции с помощью этих графиков (Рис. 1, 2).

Первой характеристикой этой динамики является факт наличия или отсутствияпромежутка значений численности N, в котором N’ > 0, то есть популяция развивается.

При отсутствии такого промежутка популяция затухает, темп затухания будет лучше виден впоследствии на временном графике.

Но будем рассматривать в основном оптимистичные сценарии.

При наличии промежутка развития в качестве характеристик области и темпа развития используем следующие параметры фазового портрета (см. Рис. 2):

- N(пор) - пороговое значение относительной численности популяции, превышение которого

ведет к росту популяции, а недостижение которого - к ее затуханию;

- N’(m) - максимальный темп роста популяции,

- N(m) - относительная численность, при которой этот экстремум достигается,

- N(ар) - емкость ареала обитания популяции, относительная численность популяции, при

достижении которой меняется знак производной N’.

Рассмотрим вопрос об устойчивости стационарных точек фазовой плоскости с координатами (N(пор),0) и (N(ар),0).

Пусть в исходном состоянии N=N(пор), N’=0 (первая стационарная точка).

Пусть теперь по каким-то причинам возникло малое отклонение N от N(пор)истало N=N(пор)+∆N.

При этом возникло и отклонение производной ∆N’. Как видно из графика на Рис. 2, последнее отклонение таково, что sign(∆N’)=sign(∆N).

Отклонение производной от N, имеющее один знак с отклонением N, приведет к дальнейшему росту (по модулю) этого отклонения.

Если исходное ∆N>0, то и ∆N’>0, и изображающая точка на фазовой кривой будет двигаться вправо до N=N(ар).

Если же исходное отклонение ∆N<0, то и ∆N’<0, и изображающая точка будет двигаться влево, к началу координат.

Таким образом, малые отклонения изображающей точки от стационарной точки (N(пор),0) ведут к дальнейшему нарастанию отклонений.

Следовательно, эта стационарная точка неустойчива.

Вторая стационарная точка (N(ар),0) устойчива.

Действительно, как видно из фазовой кривой, малое отклонение ∆N=N-N(ар) приводит к возникновению ненулевой производной ∆N’, такой, что sign(∆N’)=-sign(∆N).

Последнее предопределяет возврат изображающей точки к исходной стационарной.

Стационарные точки, будучи точками стабильности относительной численности популяции, разделяют ось этой численности на промежутки:

1) 0<=N<N(пор) - промежуток затухания популяции до 0;

2) N(пор)<N<N(ар) - промежуток роста относительной численности популяции до N(ар);

3) N>N(ар) - промежуток затухания относительной численности популяции до N(ар).

Отметим, что ненулевые (отличные от начала координат) стационарные точки мальтузианской функции и фазового портретасовпадают.

Теперь перейдем непосредственно к другому исследованию:

4. Исследование зависимости динамических свойств популяции

от ее параметров.

В качестве показателей динамических свойств популяции, определяемых с помощью ее фазового портрета и мальтузианской функции, используем следующие величины:

- пороговая относительная численность популяции N(пор.),

- емкость ареала или предельное установившееся значение относительной численности

N(ар.),

- значение относительной численности популяции в точке, где производная от этой

численности максимальна, N(m),

- максимальное значение производной от относительной численности популяции

N’(m)=Nprime(m).

В качестве параметров, влияние которых оценивается, примем описанные выше коэффициенты: NChild, Narc, Commun, QLife, Contest.

Рекомендуемый следующий порядок вычислительного эксперимента.

1.- Установите «стандартные» значения параметров,

- с помощью программы EL12Maltus постройте графики, показанные на Рис. 1 и 2,

- приближенно определите и занесите в строку «эксперимент №1» таблицы 1

(приложение 5) величины четырех выбранных показателей динамических свойств

популяции: N(пор.), N(ар.), N(m), N’(m).

Пятый столбец таблицы показателей пока остается свободным.

2.- Выберите три различных значения параметра NChild: (NChild(1), NChild(2) и

NChild(3)), вместе со «стандартным» перекрывающие рекомендованный или

выбранный вами самостоятельно диапазон варьирования этого параметра.

- Поочередно вводя эти значения, постройте на компьютере графики вида показанных

на Рис. 1 и 2 для каждого значения параметра приближенно определите величины

четырех выбранных показателей динамических свойств популяции и занесите их

в строки «эксперимент №21», «эксперимент №22» и «эксперимент №23».

3. Восстановите стандартный набор параметров популяции в программе (!).

4.- По данным экспериментов 1 и 21 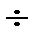23 постройте графики зависимости показателей

динамических свойств популяции от рассматриваемого ее параметра:

N(пор.)(NChild), N(ар.)(NChild), N(m)(NChild), N’(m)(NChild).

- Сделайте выводы о характере влияния.

Далее:

Задание п.2 следует четырежды,

каждый раз увеличивая на единицу первую цифру номера эксперимента и заменяя параметр популяции следующим в списке:

NChild, Narc, Commun, QLife, Contest.

В каждом эксперименте варьируется относительно «стандартных» значений лишь один параметр, остальные сохраняются «стандартными».

5.- Выберите три различных значения параметра Narc (Narc(1), Narc(2), Narc(3)),

вместе со «стандартным» перекрывающие рекомендованный или выбранный вами

самостоятельно диапазон варьирования этого параметра.

- Поочередно вводя эти значения, постройте на компьютере графики вида показанных

на Рис. 1 и 2 для каждого значения параметра приближенно определите величины

четырех выбранных показателей динамических свойств популяции и занесите их в

строки «эксперимент №31», «эксперимент №32» и «эксперимент №33».

6. Вновь восстановите стандартный набор параметров популяции в программе.

7.- По данным экспериментов 1 и 31 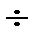33 постройте графики зависимости показателей

динамических свойств популяции от рассматриваемого ее параметра:

N(пор.)(Narc), N(ар.)(Narc), N(m)(Narc), N’(m)(Narc).

- Сделайте выводы о характере влияния.

8.- Выберите три различных значения параметра Commun (Commun(1), Commun(2),

Commun(3)), вместе со «стандартным» перекрывающие рекомендованный или

выбранный вами самостоятельно диапазон варьирования этого параметра.

- Поочередно вводя эти значения, постройте на компьютере графики вида,

показанных на Рис. 1 и 2 и для каждого значения параметра приближенно

определите величины четырех выбранных показателей динамических свойств

популяции и занесите их в строки «эксперимент №41», «эксперимент №42» и

«эксперимент №43».

9. Восстановите стандартный набор параметров популяции в программе.

10. -По данным экспериментов 1 и 41 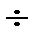43 постройте графики зависимости

показателей динамических свойств популяции от рассматриваемого ее параметра:

N(пор.)(Commun), N(ар.)(Commun), N(m)(Commun), N’(m)(Commun).

- Сделайте выводы о характере влияния.

11. -Выберите три различных значения параметра QLife (QLife(1), QLife(2), QLife(3))

вместе со «стандартным» перекрывающие рекомендованный или выбранный вами

самостоятельно диапазон варьирования этого параметра.

- Поочередно вводя эти значения, постройте на компьютере графики вида

показанных на фиг. 1 и 2 для каждого значения параметра приближенно

определите величины четырех выбранных показателей динамических свойств

популяции и занесите их в строки «эксперимент №51», «эксперимент №52» и

«эксперимент №53».

12. Восстановите стандартный набор параметров популяции в программе.

13. -По данным экспериментов 1 и 51 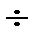53 постройте графики зависимости

показателей динамических свойств популяции от рассматриваемого ее параметра:

N(пор.)(QLife), N(ар.)(QLife), N(m)(QLife), N’(m)(QLife).

- Сделайте выводы о характере влияния.

14. -Выберите три различных значения параметра Contest (Contest(1), Contest(2),

Contest(3)), вместе со «стандартным» перекрывающие рекомендованный или

выбранный вами самостоятельно диапазон варьирования этого параметра.

- Поочередно вводя эти значения, постройте на компьютере графики вида

показанных на Рис. 1 и 2 для каждого значения параметра приближенно

определите величины четырех выбранных показателей динамических свойств

популяции и занесите их в строки «эксперимент №61», «эксперимент №62» и

«эксперимент №63».

15. Восстановите стандартный набор параметров популяции в программе.

16. -По данным экспериментов 1 и 61 63 постройте графики зависимости

показателей динамических свойств популяции от рассматриваемого ее параметра:

N(пор.)(Contest), N(ар.)(Contest), N(m)(Contest), N’(m)(Contest).

- Сделайте выводы о характере влияния.

17. Анализ переходных процессов в популяции.