Понятия и основные элементы графика.

В практике с. материалы таблицы удачно дополняют графики. Статистический график – наглядное изображение и обобщение данных при помощи геометрич. образов, знаков или геогр-х картосхем. Главное их достоинство – наглядность (80% информации воспринимается глазами). Показатели через графическое изображение становятся понятными, выразительными, лаконичными и запоминающими. Графики прочно вошли в повседневную работу экономистов и статистов=> надо уметь их правильно строить и читать. В настоящее время разработаны пакеты прикладных программ компьютерной графики, кот. облегчает задачу исследователя в практическом применении графика. Наиб. распространенными пакетами прикладных программ явл. Harvard grathics, Statgraf, Supercalc, Excel. Основными элементами графика явл. след.: Поле графика – пространство, где размещаются геометрич. знаки или образы, образующие график. Оно характ-ся размером и пропорцией. Размер должен соответствовать назначению. Напр. лекция, доклад, книга. Пропорции должны соответствовать нашим представлениям о гармонии. Этому в наиб. степени удовлет-т графики с неравными сторонами. Наилучшее соотношение масштаба по осям 1,66:1, называемое золотым сечением. Это 5/3 или 8/5. В практике применяют форматы с соотношением сторон 1:1,3 – 1:1,5. Этому соответ-но соотв-т формат бумаги 814 на 1152 мм. Во многих сл. удобным явл. квадратные графики. Геом. знаки или образы – знаки, с пом. кот. изображаются статистические величины. Это м. б. отрезки прямых линий, точки, квадраты, прямоугольники, круги или фигуры. Знак – основа графика. Поэтому очень важно его выбрать. Пространственные ориентиры, размещение геометр. знаков, поле графика задаются системой координатных сеток или контурных линий, кот. делят это поле на части. Применяются декартовые или полярные координаты. Криволинейные контурные линии применяются в статистических картах. Напр. границы районов, гос-в и т.д. Масштабные ориентиры определяются системой масштабных шкал, которые бывают равномерные и неравномерные. Чаще применяются равномерные шкалы. Экспликация графика – словесное пояснение его содержания. Включает название графика, подписи масштабных шкал, ед-цы измерения и условные обозначения. Название графика должно в краткой форме передавать его содержание

Понятие и сущность средних величин (СВ).

Абсолютные и относительные величины имеют важное значение в статистике, но для анализа этих показателей не достаточно. Статистика исследует признаки массовых явлений, которые различаются по величине. Напр. ст. по возрасту, рабочие по стажу работы и з/п. С одной стороны мы имеем много показателей, и с ними трудно работать. С другой – размеры признаков для каких-то условий явл. характерными. Размеры признака, характерные для массы единиц статистика измеряет при помощи средних величин(СВ). СВ – обобщающая характеристика совокупности однотипных явлений по одному кол-му признаку. Метод СВ явл. одним из важнейших статист. методов. СВ дает возможность охарактеризовать общие черты и свойства массовых явлений, закономерность их развития. СВ отражает достигнутый уровень. На массовые процессы влияют 2 группы причин: Причины, отражающие состояние массовых процессов; СВ, связанные с особенностями отдельных единиц совокупности. Это влияние при большом числе наблюдений взаимопогашается. При расчете СВ следует соблюдать ряд условий. Их следует рассчитывать и сопоставлять для качественно однородных единиц. Напр. Показатели работы общественных и специализированных организаций. При большом различии показателей следует проводить группировку. Среднее погашает индивидуальные различия у ед. совокупности - недостаток. Поэтому надо определять не только средние, но min и max-ые размеры показателей. Средние, рассчитанные по совокупности в целом, наз. общие средние. А исчисленные по гр. наз. групповой средней. Средние широко применяются в управлении отраслями, при планировании, при контроле выполнения плана.

Виды средних.

Сущ. 2 категории средних: Степенные средние, структурные или описательные средние (показательный центр распределения). К степенным средним относятся: среднее арифметическое;среднее гармоническое; среднее квадратическое; среднее геометрическое. Расчет этих средних выражается математически. Общая формула степенной средней: 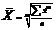, x – отдельное значение признака, 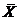- степенная среднее, n – число единиц, m – показатель степени средней. Среднее арифм-ое, гарм-ое и квадратическое м. б. простыми, если каждое отд-ое знач-е признака встречается только один раз и взвешенными – если несколько раз. Соотв-но формулы средних:

	простые	взвешенные
Ср. арифм. m=1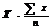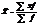
Ср. гарм.m=-1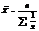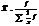
Ср. квадр.m=2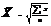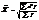
Ср. геом. m=0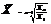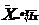

П – произведение; x – темпы роста

Эти степенные средние, исчисленные для одной совокупности единиц, имеют различное количественное значение. И чем > показатель степени m, тем > величина средней.

Это св-во средних наз. мажоратностным средним. Применение вида средних определяется материальным содержанием изучаемых явлений. Наиб. часто применяется среднее арифметическое и гармоническое.

Среднее геометрическое применяется при исчислении средних темпов динамики, а среднее квадратическое для характеристики вариации признака. Можно определить еще одну среднюю – среднюю прогрессивную.

Напр. Имеем след з/п рабочих: 105, 115, 130, 140, 155, 170, 190

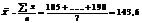Общий подход: определяют прогрессивное направление показателей: какая з/п лучшая. Отбрасываем все значения з/п < 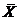. А для оставшихся рабочих определяем среднюю прогрессивную.

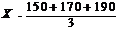
5.3.Свойство средней арифметической.

Среднее арифметическое имеет ряд свойств, которые определяют ее широкое применение в экономических расчетах и в практике статистического исследования: 1. Среднее арифметическое постоянной величины = этой постоянной: А=А при А=const. 2. Алгебраическая сумма отклонений индивидуальных значений от средней арифметической =0. 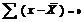. 3. Сумма квадратов отклонений индивидуальных значений признаков от средней арифметической – есть число min: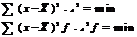

Второе и з-е свойства могут использоваться для проверки правильности расчета средней. Кроме того существуют свойства средней, имеющие прикладное значение, так называемые, расчетные свойства: а) если значение признака каждой единицы уменьшить или увеличить на постоянное число, то среднее уменьшится или увеличится на тоже число; б) если значение признака каждой единицы разделить или умножить на постоянное число, то среднее арифметическое уменьшится или увеличится во столько же раз; в) если частоту каждого значения признака разделить или умножить на какое-либо постоянное число, то среднее не изменится. Перечисленные св-ва можно использовать для облегчения расчета средней. Заключение: В настоящее время расчетные св-ва средней арифметической несколько утратили свою актуальность в связи с использованием электронной вычислительной техники при расчете обобщающих показателей.

Другие виды средних.

Среднее гармоническое применяется тогда, когда известны индивидуальные значения признака и общий объем совокупности, но не известны частоты. Напр. необходимо рассчитать среднюю з/п треста по след. данным:

№СУ	Фонд з/п ,Ф=xf	Число рабочих, f	Средняя з/п x
Итого			-

При наличии таких данных рассчитываем среднюю з/п:

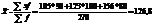Если Ф, x – известны, f нет, тогда:

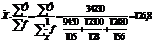
6.1.Понятие о вариации признаков.

Вариацией признака назыв.его измен. у ед.совокупности. Рабочие различаются по возрасту, по стажу работы. Вариация порождается комплексом разнообразн.усл., воздействующих на эл.совокупн. Напр.вариация оценок на экзам. порождается различиями способностей студ., соц.быт.усл. Если бы все студ.получали бы одинаков.оценки, то необходимость в ст-ке отпала бы. Влияющие факторы можно разделить на внутрен.и внешние, необход.и случайные. Их действия переплетены. Поломка машины может снизить производит.труда, но если будет резервная машина, то этого не произойдет, значит необходимость оказывает регулирующее значение на случайные факторы. Мерой вариации в некоторой степ.явл.СВ. Но при одинак.средней размеры вариации могут существенно отличаться друг от друга, поэтому для хар-ки распределения необходимы показатели степени вариации.

Ряды распределения.

В процессе группировки произв. распределен. ед.савокупности по значен-ям группировочн.признака, в результате чего получаются две колонки, одна из кот. содержит перечень значений признака, а другая - данные изучаемых ед. Такое распред.ед.совокупности по значениям групп.признака назыв. рядом распределения. Ряды распределен. могут быть образованы по качествен. признакам(назыв.атрибутивными) либо по количествен.(вариацион.). Напр.качествен.-распределен.раб. по полу, а вариац.-распределен.раб по стажу. Различают дискретные и интервальные вариац.ряды. Чаще примен.интервальн.вариац.ряды. При их построен.следует соблюдать ряд усл.:1)гр.и подгр. должны существенно отличаться друг от друга.,2)лучше применять не равные интерв., но примен равн.интерв. дает возможность исп.матем.приемы анализа явлен. 3)чем больше колеблемость признака, тем больше должно быть групп. Абсолютные численности интервалов называют частотами, а сумму всех частот его объемом.Частоты выражен.в долях и % к объему ряда назыв. частотностями. В интервальн. рядах с неравн. интервалами непосредствен. сравнение численности отдельных групп затруднено, т.к. меняются и интервалы и их численность. В этом случае определяют плотность распределения. Плотность – это отношение частот или частотностей к величине интерв. Плотность распределен.может быть абсолютн.(если рассчитана на основе частот) и относит.(если рассчитана по частотностям). Частоты в вариац.рядах с равными интерв.и плотность распределен.в рядах с неравн.интерв.выражает определен. закономерность в распределен. Для их хар-ки могут быть исп.и накопленные частоты. Накоплен.частоты для каждого интервала рассчитываются путем последоват.суммирования частот всех интервалов. Их можно рассчитать в восход.и нисход. порядке.

Гр.по з/пл Тыс.р.	Число Раб.	Накоплен.частоты
Восход порядок	Нисход. порядок
до 100
100-150		8+25=33
150-250			170-110=60
250и более
Итого:

Т.е. у 33 раб з/пл не превышает 150 тыс.р., или у 170 раб. з/пл не ниже 150 тыс.р.