Условная классическая вероятность. Свойства.
Вероятность события при условии, что произошло другое событие, называется условной вероятностью: p(A/B), p(A)
Свойства:
1. p(Ω/c)=p(Ωc)/p(c)=1
2. p(Ø/c)=p(Øc)/p(c)=0
3. AB≠Ø
p(A+B/c) 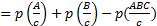
4. AB=Ø
p(A+B/c)= 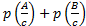
5. BcA
p(A/C)≤p(B/C)
6. p(A/C)?[0,1]
7. p(A/C)=1-p(Ā/C)
Статистическая вероятность. Ее аксиомы.
Значение относительной чистоты, полученное при бесконечном числе испытаний 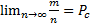 , называется статистической вероятностью.
, называется статистической вероятностью.
Аксиомы:
1. m/n≥0
2. m=n à m/n=1
3. m=m1+m2 à m/n=m1/n=m2/n
Алгебра события. Замкнутость алгебры относительно основных операций.
Пусть дано бесконечное пространство Ω. Ω={w1, w2, …, wn}. Образуем множество всех подмножеств этого пространства δ-алгебра и придадим следующие свойства:
· Ω?δ-алгебра
· A1•A2?δ-алгебра à A1+A2?δ-алгебра
· A? 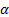 à Ā?δ-алгебра
à Ā?δ-алгебра
Теорема о замкнутости.
· A1,A2?δ-алгебра à A1+A2?δ-алгебра
· A1,A2?δ-алгебра à A1•A2?δ-алгебра
· A1,A2?δ-алгебра à A1-A2?δ-алгебра
· Симметрическая разность
A1,A2?δ-алгебра à A1∆A2?δ-алгебра
Формулировка аксиоматической вероятности.
Пусть дано бесконечное пространство Ω. Ω={w1,w2…wn}. Образуем множество всех подмножеств этого пространства А и обладающие определенными свойствами.
Свойства аксиоматической вероятности.
1. p(Ω)=1
2. p(Ø)=0
3. если события A и B несовместны, то p(A+B)=p(A)+p(B)
4. p(A+B)=p(A)+p(B)-p(AB)
5. Событие A инициазирует событие B
AсB à p(A)≤p(B)
6. Следует из предыдущих свойств
p(A)?[0,1]
7. p(Ā)=1-p(A)
Теорема сложения событий (аксиоматическая вероятность).
AB≠0
p(A+B)=p(A)+p(B)-p(AB)
Теорема умножения событий.
A1, A2, … , An ? δ-алгебра
p(A1 • A2 • … • An)=p(A1)•p( 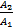 )•p(
)•p( 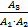 )•…•p(
)•…•p( 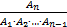 )
)
Вероятность появления хотя бы одного события.
Пусть даны события A1, A2, … An независимы в совокупности
B=Ā1•Ā2•…•Ān ( не произошло ни одного события)
Введем событие A=A1+ A2+ … +An (произошло хотя бы одно событие)
A+B=Ω
A•B=Ø
Рассмотрим формулу и вероятность на ней
p(A+B)=1
p(A)+p(B)=1
p(A)=1-p(Ā1,Ā2,…Ān)=1-p(Ā1)…p(Ān)
p(Āi)=qi
qi=1-pi
pi=p(Ai)
è p(A)=1-q1q2…qn – вероятность появления хотя бы одного события
Формула полной вероятности и формула Байеса.
Формула полной вероятности
p(A)= 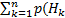 )•p(A/
)•p(A/ 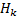 )
)
Формула Байеса

Схема испытаний Бернулли.
Система независимых испытаний, где в каждом опыте системы события появляются с постоянной вероятностью, называют схемой испытаний Бернулли:
Pn(m)= 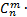 pm
pm  qn-m
qn-m
Наивероятнейшее число событий, оценка н.ч.с.
Значение числа событий, при котором достигается их наивероятнейшее значение, называют наивероятнейшим числом событий.
Теорема ( о наивероятнейшем событии)
Пусть реализуется схема Бернулли в n испытаниях, p вероятностей
q=1-p
то НЧС заключается в следующих границах:
m*: np-q≤m*≤np+q
при этом имеет место 3 случая:
· если np-q дробное, то m* - единственно
· если np-q целое положительное, то m* и m*+1
· если np целое, то m* - единственное и совпадает с np: m*=np
