Круговое свойство дробно-линейной функции.
W=az+b/cz+d ; - дробно-линейное отображение (a,b,c,d – комплексные числа) Теорема. При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая. □  w=a*z+b
w=a*z+b
рассмотрим: Это отображение сводится к подобию, повороту и переносу. Следовательно, окружности в окружности а прямые в прямые. При W=az+b/cz+d не линейной (коэфф С не нулевой) представим ее в виде W=A+B/z+z0 где A=a/c;B=(bc-ad)/c2;z0=d/c. Тогда отображение сводится к последовательному выполнению след отображений:
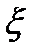 =z+z0 ;
=z+z0 ; 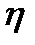 =1/
=1/ 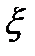 ; w=A+B
; w=A+B 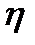 ; Первое и третье обладают круговым свойством в силу линейности. Докажем что и w=1/z обладает этим свойством. Уравнение любой окружности или прямой на комплексной плоскости имеет вид
; Первое и третье обладают круговым свойством в силу линейности. Докажем что и w=1/z обладает этим свойством. Уравнение любой окружности или прямой на комплексной плоскости имеет вид 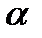 (x2+y2)+
(x2+y2)+ 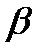 x+
x+ 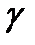 y+
y+ 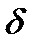 =0; (при
=0; (при 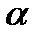 =0 это уравнение прямой) x2+y2=|z|2=z
=0 это уравнение прямой) x2+y2=|z|2=z 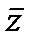 ; x=1/2(z+
; x=1/2(z+ 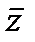 ); y=1/2i(z-
); y=1/2i(z- 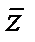 ); уравнение теперь имеет вид
); уравнение теперь имеет вид 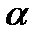 z
z 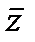 +Dz+
+Dz+ 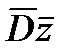 +
+ 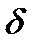 =0; где D=1/2(
=0; где D=1/2( 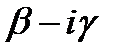 ) подставляем в w=1/z и получаем
) подставляем в w=1/z и получаем
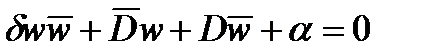 Следовательно образом окружности (или прямой при
Следовательно образом окружности (или прямой при 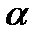 =0)
=0)
При отображении w=1/z является окружность (прямая при 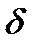 =0) ■ Отметим что W=az+b/cz+d переводит окружности и прямые, проходящие через z0=-d/c в прямые, а остальные окружности и прямые – в окружности. Прямай – это окружность бесконечного радиуса – следовательно все окружности переходят в окружности J
=0) ■ Отметим что W=az+b/cz+d переводит окружности и прямые, проходящие через z0=-d/c в прямые, а остальные окружности и прямые – в окружности. Прямай – это окружность бесконечного радиуса – следовательно все окружности переходят в окружности J
+27. Принцип сохранения симметрии при дробно-линейном отображении.
Точки M и M* симметричные относительно окружности Г, если они лежат на одном луче, выходящем из O, и OM х OM*=R2; Каждая точка окружности симметрична сама себе относительно окружности.
Теорема. При дробно-линейном отображении пара точек, симметричных относительно окр, переходят в пару точек, симметричных относительно образа этой окр. Здесь окружность может быть в частности и прямой. Чтобы доказать теорему надо сначала доказать лемму.
Лемма: Точки M и M* являются симметричными тогда и тока тогда, когда любая 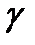 - окружность, проход через точки, пересекается и Г под прямым углом.
- окружность, проход через точки, пересекается и Г под прямым углом.
□Необходимость. Пусть M, M*симм относительно Г радиуса R с центром в O. Рассмотрим 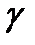 проходящую через M и M*, проведем из O прямую, касающуюся
проходящую через M и M*, проведем из O прямую, касающуюся 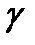 в точке P. Т.к. квадрат касательной равен произведению секущей на ее внешнюю часть то OP2=OMxOM*. Так как точки симметричны относительно Г то OP=R, следовательно окружности пересекаются под прямым углом. ■
в точке P. Т.к. квадрат касательной равен произведению секущей на ее внешнюю часть то OP2=OMxOM*. Так как точки симметричны относительно Г то OP=R, следовательно окружности пересекаются под прямым углом. ■
□Достаточность. Любая окружность 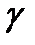 проходящая через M и M* пересекается с Г под прямым углом, тогда и любая прямая (частный случай окружности) проход через две эти точки, тоже пересекает Г под прямым углом. Значит прямая проходит центр окружности O. Более того, точки M и M* лежат на одном луче, выходящем из O, так как в противном случае окружность радиуса ½ MM* не пересекала бы Г под прямым углом. Докажем что OM х OM*=R2 : Пусть окружности пересекаются в точке P, тогда OP – касательная к
проходящая через M и M* пересекается с Г под прямым углом, тогда и любая прямая (частный случай окружности) проход через две эти точки, тоже пересекает Г под прямым углом. Значит прямая проходит центр окружности O. Более того, точки M и M* лежат на одном луче, выходящем из O, так как в противном случае окружность радиуса ½ MM* не пересекала бы Г под прямым углом. Докажем что OM х OM*=R2 : Пусть окружности пересекаются в точке P, тогда OP – касательная к 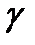 и OM х OM*=R2 (по теореме о квадрате касательной) ■
и OM х OM*=R2 (по теореме о квадрате касательной) ■
+27.Теперь имея лемму докажем Теорему о симметрии
□Пусть точки z и z* симметричны относительно Г и пусть дробно-линейное отображение w=f(z) переводит Г в 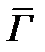 а точки z и z* в точки w и w* соответственно. В силу кругового свойства
а точки z и z* в точки w и w* соответственно. В силу кругового свойства 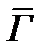 - окружность. Нужно доказать что w и w*симмотн
- окружность. Нужно доказать что w и w*симмотн 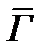 . Для этого в силу леммы достаточно доказать что любая
. Для этого в силу леммы достаточно доказать что любая
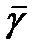 проход через эти две точки, пересекает
проход через эти две точки, пересекает 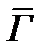 под прямым углом. Прообразом окружности
под прямым углом. Прообразом окружности 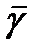
Является окружность 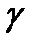 проход через z и z* и эта окружность пересекает Г под прямым углом.
проход через z и z* и эта окружность пересекает Г под прямым углом.
Следовательно, 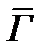 и
и 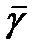 пересекаются тоже под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной комплплоскоти и сохраняет углы между кривыми в каждой точке! ■
пересекаются тоже под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной комплплоскоти и сохраняет углы между кривыми в каждой точке! ■
28. Конформное отображение дробно-линейной функцией:
а) верхней полуплоскости на единичный круг
б) единичного круга на единичный круг.
a) Imz>0 на |w|<1 имеет вид W=(z-z0/z- 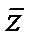 0)ei
0)ei 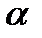 (1)
(1)
где 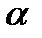 - действительно число.
- действительно число.
□Пусть дробно-линейная функция w=w(z)
Отображает полуплоскость на круг так, что w(z0)=0 (Imz0>0) Тогда в силу сохранения симметрии w( 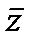 0)=
0)= 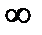 и w=A(z-z0/z-
и w=A(z-z0/z- 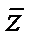 0), (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в
0), (так как всякое дробно линейное отобр, переводящее точку z1 в 0 а z2 в 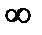 равно w=A(z-z1/z-z2) )
равно w=A(z-z1/z-z2) )
покажем что |A|=1. Так как точки действительной оси переходят в точки единичной окружности, то есть |w|<1 при действительныхz=x то
1=|A(z-z0/z- 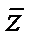 0)|= |A| (так как z-z0=z-
0)|= |A| (так как z-z0=z- 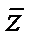 0) Следовательно A=ei
0) Следовательно A=ei 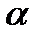 ■ Всякое комфорное отображение имеет именно вид (1) – так как по теореме Римана существует единственное такое отображение, удовлетворяющее условиям.
■ Всякое комфорное отображение имеет именно вид (1) – так как по теореме Римана существует единственное такое отображение, удовлетворяющее условиям.
б) |z|<1 на круг |w|<1 имеет видw=(z-z0/1-z 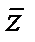 0)ei
0)ei 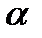 (1)
(1)
где 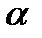 - действительно число.
- действительно число.
□Пусть дробно-линейная функция w=w(z) отображает круг |z|<1 на круг |w|<1 так, что w(z0)=0 Тогда в силу сохранения симметрии w(1/ 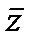 0)=
0)= 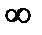 и имеем w=A(z-z0/1-z
и имеем w=A(z-z0/1-z 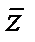 0) (так как всякое дробно линейное отобр, переводящее точку z1 в 0, а z2 в
0) (так как всякое дробно линейное отобр, переводящее точку z1 в 0, а z2 в 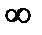 равно w=A(z-z1/z-z2) ) . Покажем что |A|=1. Так как точки единичной окр переходят в точки едокр, то 1=|A(ei
равно w=A(z-z1/z-z2) ) . Покажем что |A|=1. Так как точки единичной окр переходят в точки едокр, то 1=|A(ei 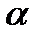 -z0/1-ei
-z0/1-ei 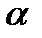 *
* 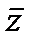 0)|=|A| (так как | ei
0)|=|A| (так как | ei 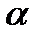 -z0|=|e-i
-z0|=|e-i 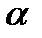 -
- 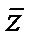 0|)Следовательно A=ei
0|)Следовательно A=ei 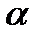 ■
■
29. Конформные отображения элементарными функциями (z2,zn,√z, n√z).
a) w=z2 = R2ei2 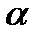 . Однолистная в области, когда в области нет точек связанных равенством z1=-z2 (нет ни одно пары точек, симметричных относительно z=0)
. Однолистная в области, когда в области нет точек связанных равенством z1=-z2 (нет ни одно пары точек, симметричных относительно z=0)
Образы лучей argz= 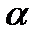 и дуг окружностей |z|=
и дуг окружностей |z|= 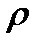 . Линии argz=const и |z|=const образуют координатную сетку на плоскости z. (полярные координаты)
. Линии argz=const и |z|=const образуют координатную сетку на плоскости z. (полярные координаты)
Образы прямыхRez=с и Imz=с Взаимо однозначно переводит Rez=с в параболу v2=2p(p/2-u) а прямую Imz=с в параболу v2=2p(u+p/2) здесь p=2c2; w=u+iv;
б) w= 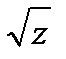 Обратная к функции w=z2 : аналитическая плоскости z с выколотыми z=0,
Обратная к функции w=z2 : аналитическая плоскости z с выколотыми z=0, 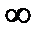 ,а в плоскости с разрезом, соединяющим 0 и
,а в плоскости с разрезом, соединяющим 0 и 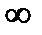 , распадается на две регулярные ветви.
, распадается на две регулярные ветви.
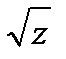 =
= 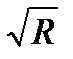 ei(
ei( 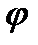 +2
+2 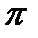 k)/2
k)/2
в) w= 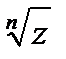 =|
=| 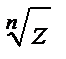 | ei(
| ei( 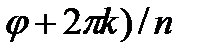
30. Конформные отображения функциями еz, Lnz, функцией Жуковского.
а)W=1/2(z+1/z) - функция регулярна в точках кроме 0 и 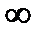 причем
причем 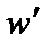 (z)=1/2(1-1/z2) а в точках z=0 и z=
(z)=1/2(1-1/z2) а в точках z=0 и z= 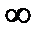 полюсы первого порядка. Однолистна в след областях
полюсы первого порядка. Однолистна в след областях
1-|z|>1
2-|z|<1
3-ImZ>0
4-ImZ<0
б)W=ez =ex+di=|ex|ediw=eceiyc=0 – единичная окружность c<0 – единичный круг, c>0 – внешнось
в)W=LnZ=ln|z|+iargz+2 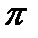 ki ;
ki ;
