Почленное интегрирование РСФР
Теорема 1. ( почленное интегрирование РСФР): Пусть члены 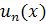 ФР
ФР 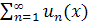 непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b].
непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. 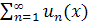 ,
, 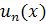 - непрерывны на[a;b]. Тогда ФР можно интегрировать почленно:
- непрерывны на[a;b]. Тогда ФР можно интегрировать почленно:  .
.
( Так как 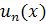 , S(x) (в силу теоремы 1) - непрерывны на [a;b], то
, S(x) (в силу теоремы 1) - непрерывны на [a;b], то 
Докажем: 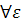 >0
>0  >
> 

 =
= 
(т.к. из равномерной сходимости ФР  >0
>0  =
=  :
:  x
x  [a;b],
[a;b],  n>
n> 
 |S(x)-
|S(x)-  |<
|<  )
)
Замечание 1: В теореме 1 интегрирование можно проводить по любому отрезку [a,x], где x  [a;b]
[a;b]

Замечание 2:  =
= 
Почленное дифференцирование РСФР
Теорема (о почленном дифференцирование РСФР):Пусть  непрерывно дифференцируемы на [a;b].
непрерывно дифференцируемы на [a;b].
ФР (1)  сходится на [a;b], (2)
сходится на [a;b], (2)  равномерно сходится на [a;b].
равномерно сходится на [a;b].
Тогда 
(Обозначим P  =
=  . Из теоремы 3 следует:
. Из теоремы 3 следует:  =
=  ;
;
 =
=  =
= 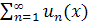 -
- 
 = S(x)-S(a). ПотеоремеБарроу: (
= S(x)-S(a). ПотеоремеБарроу: (  )´=P(x)=S´(x) ).
)´=P(x)=S´(x) ).
Замечание:  = (
= ( 
16.Предел последовательности комплексных чисел. Необходимое и достаточное условия.
Комплексное число  является пределом
является пределом 



Критерий сходимости: для того, чтобы 

(  )
) 
 и
и 
(Н)
 :
: 







(Д)
 ;
; 






 ;
; 


17.Кривые и области комплексной плоскости. Основные определения.
· t  f(t)=x(t)+iy(t) – комплекснозначная функция от действительной переменной
f(t)=x(t)+iy(t) – комплекснозначная функция от действительной переменной
· f(t) непрерывна на  если x(t) и y(t) непрерывны на
если x(t) и y(t) непрерывны на 
· f’(t)=x’(t)+iy’(t) : f(t) дифференц. на  если x(t) и y(t) дифференц. на
если x(t) и y(t) дифференц. на 
· Теорема: если на  задана непрерывная z=f(t) то говорят что задана непрерывная кривая a=f(a) и b=f(b) – концы. Кривая замкнута если a совпадает с b.
задана непрерывная z=f(t) то говорят что задана непрерывная кривая a=f(a) и b=f(b) – концы. Кривая замкнута если a совпадает с b.
· Z1=f(t1) Z2=f(t2) если t1 неравно t2 а Z1=Z2 и хотя бы одна из z не является ни a ни b то это точка самопересечения
· Криваяне содержащая точек самопересечения называется простой (жардановой)
· Если накривой  то она называется гладкой
то она называется гладкой
· Замкнутая простая кусочногладкая кривая называется контуром
· Точка z0 является внутренней точкой множества D если  которая целиком лежит в D
которая целиком лежит в D
· Множество состоящее из внутренних точек называется открытым
· Множествоназывается связнам если две его точки можно соединить непрерывной кривой лежащей в нём
· Множество D – область если оно открытое и связное
· Областьограниченная γ обозначается D γ и называется контуром
· Область с присоединенной границей называется замкнутой
· Точка z0 – изолированная если  в которой нет точек кроме неё самой
в которой нет точек кроме неё самой
· Область называется односвязной если замкнутую непрерывную кривую можно стянуть в точку не выходя за пределы области
Предел и непрерывность Функции Комплексной Переменной

Пусть W() однозначно определена в окружности z0

 если :
если :
1) 

2) 

Используя критерий сходимости комплексной последовательности (16)запишем




Основные элементарные ФКП
1) линейная w=az+b – непрерывна на z
2) степенная w=zn
3) дробнолинейная 
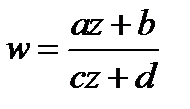
 0
0
4) w=ez=ex(cosy+isiny)
5) логорифмическая w=Lnz=ln|z|+iargz+2nki
6) тригонометрические 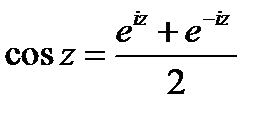
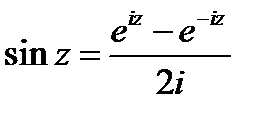
7) обратные тригонометрические cosiz=chsiniz=ish
+21.Дифференцирование ФКП. Условия Коши-Римана.
Пусть 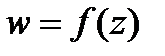 определена и одназн. в
определена и одназн. в 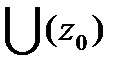 .Если
.Если 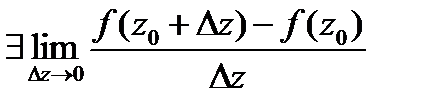
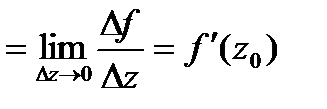 ,то ф-я дифф-ма в
,то ф-я дифф-ма в 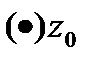 .
.
Т.е. 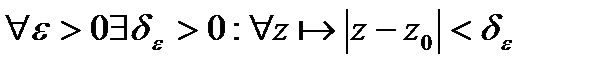
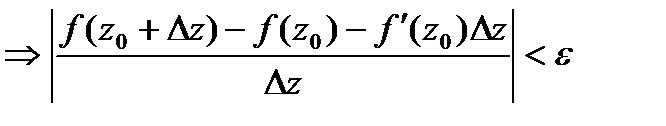
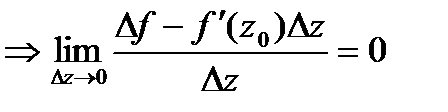 .
. 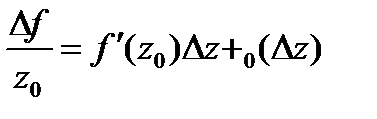 (*).
(*).
Если ф-я диф-ма в  ,то её приращение представимо в виде (*). Пусть представимо так:
,то её приращение представимо в виде (*). Пусть представимо так: 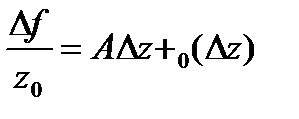 (**),
(**), 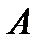 не зависит от
не зависит от 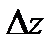 . Тогда
. Тогда 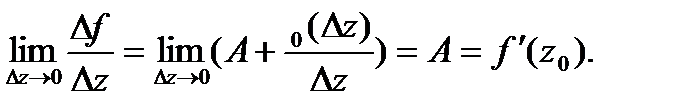 Чтобы
Чтобы 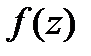 была диф-ма в
была диф-ма в 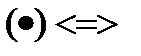 чтобы её приращ. в
чтобы её приращ. в  было в виде (*).
было в виде (*).
Если 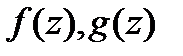 -диф-мы в
-диф-мы в 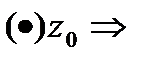 1)
1) 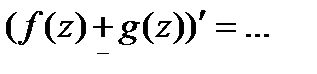
2) 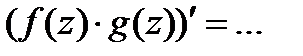 3)
3) 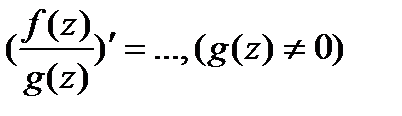 4)
4) 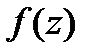 -диф-ма.в
-диф-ма.в 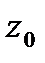
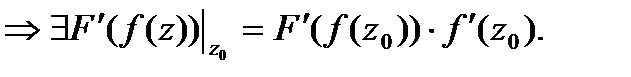 Если
Если 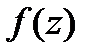 -диф. в
-диф. в 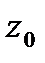 ,то
,то 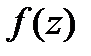 -непрерывна в
-непрерывна в 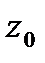 .
.
□по св-ву 1: 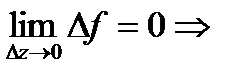 непрер. ■ Если
непрер. ■ Если 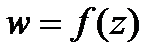 -диф. в
-диф. в 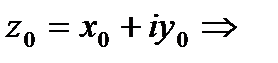
 -диф-мы в
-диф-мы в  . Обратное не всегда верно.
. Обратное не всегда верно.
+21Теорема Коши-Римана. Пусть 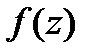 -определена и однозн.в
-определена и однозн.в 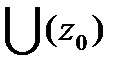 .Чтобы
.Чтобы 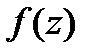 была диф-ма в
была диф-ма в 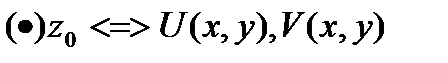 были диф-мы в
были диф-мы в 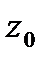 и выполнялись:
и выполнялись: 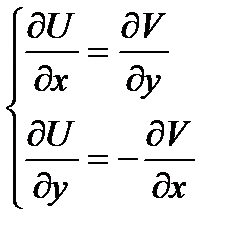 в
в 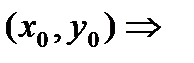
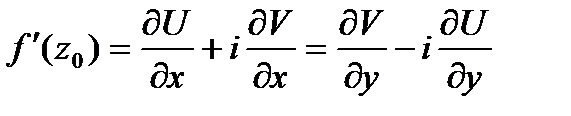 .
.
□Необ.Пусть 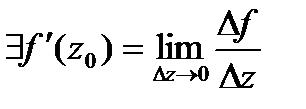 .
.
а) 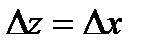 .
. 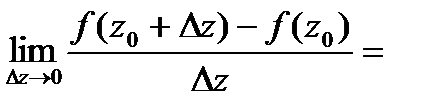
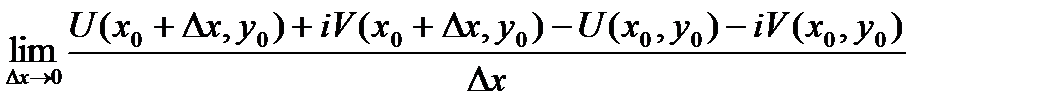
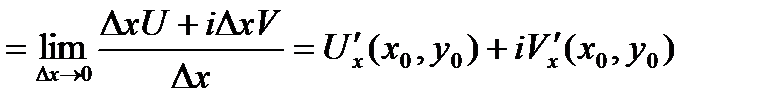 .
.
б) 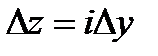 .
. 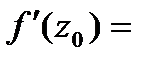
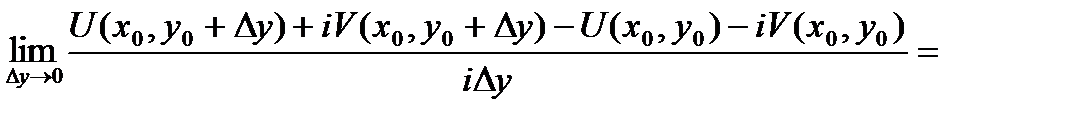
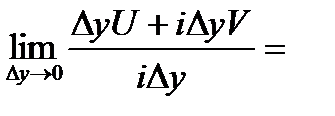
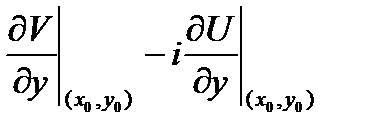 .
. 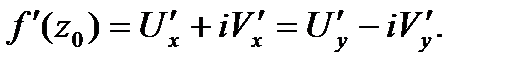
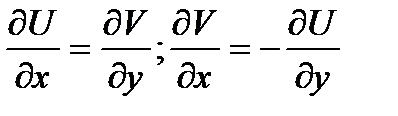 (***).
(***).
Дост. 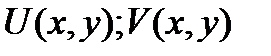 -диф-мы в
-диф-мы в 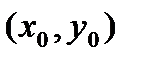 и выполняется (***).
и выполняется (***). 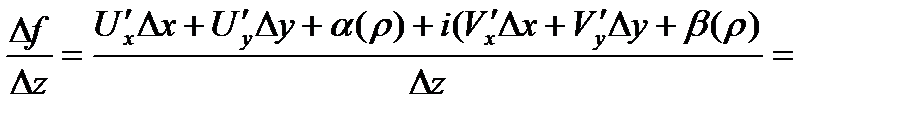
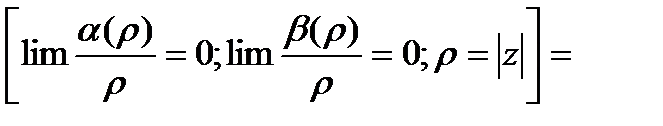
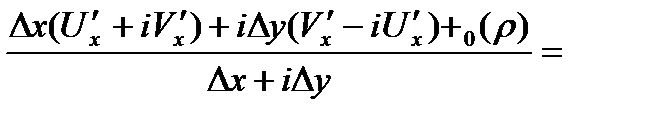
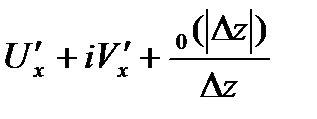 при
при 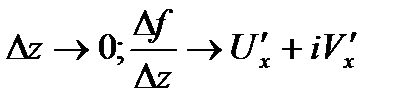 . Т.е.
. Т.е. 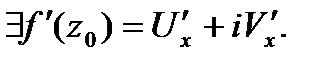 ■
■
