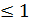Критерий Коши сходимости числовых рядов. Необходимое условие сходимости

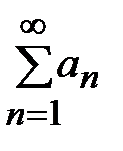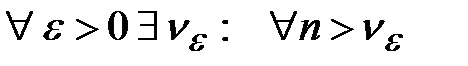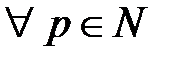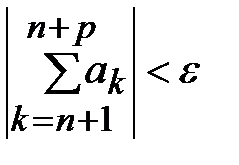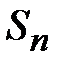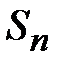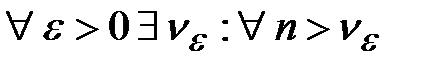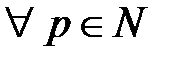Теорема (критерий Коши):Для того чтобы ряд сходился, необхо­димо и достаточно, чтобы и выполнялось бы: .{Сходимость числового ряда определяется сходимостью числовой последовательности { }. Ранее доказано: для того чтобы последователь­ность { } сходилась, необходимо и достаточно, чтобы и выполнялось бы: 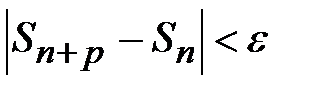или .}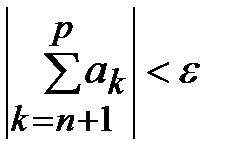

Теорема (необходимое условие сходимости) : 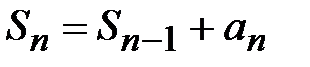. Переходя к пределу при 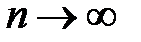, получим: 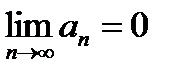. Тот же результат можно получить из критерия Коши, полагая p = 1. Очевидно, условие 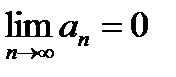является необхо­димым, но не достаточным условием сходимости числового ряда.(НО :Ряд 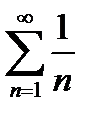расходится , однако )

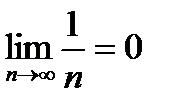Признаки сравнения числовых рядов

Теорема 1 (признак сравнения):Пусть даны два ряда: 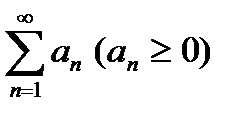(1) и 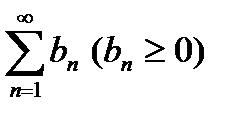(2). Если, начиная с некоторого номера выполняется: 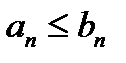(3), 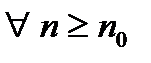, то из сходимости ряда (2) 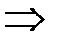сходимость ряда (1); из расходимости ряда (1) 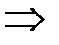расходимость ряда (2).

{Не ограничивая общности, будем считать, что неравенство 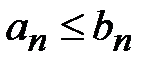вы­полняется для всех n . Пусть 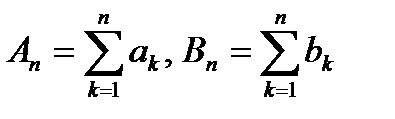. Очевидно, последовательно­ст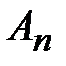и { } и { 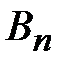} – монотонные неубывающие. Пусть ряд (2) сходится. То­гда { 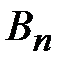} ограничена: 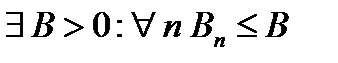. Но тогда, в силу (3), 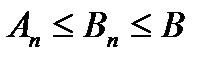и ряд (1) – также сходится.

Пусть ряд (1) расходится. Если бы ряд (2) сходился, то, по доказанному выше, сходился бы и ряд (1). Т.е. получили бы противоречие. Таким обра­зом, ряд (2) также расходится.}

Теорема 2 (признак сравнения в предельной форме):Пусть 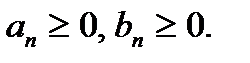Если существует 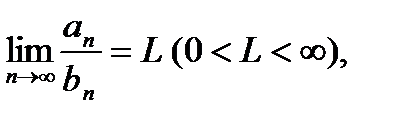то ряды (1) и (2) сходятся либо расходятся одновременно.{Пусть ряд (2) сходится.Из существования 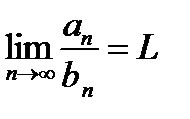: 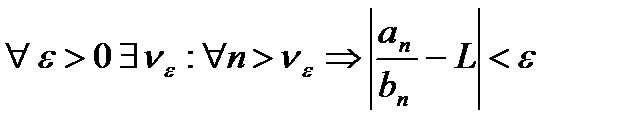, откуда получаем: 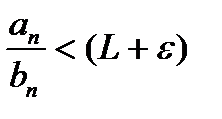или 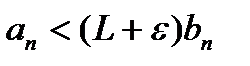следует сходимость ряда (1). Пусть ряд (2) расходится.Существует 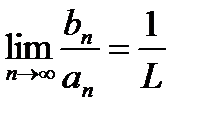, откуда аналогичным образом получаем: 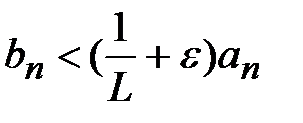. Если бы сходился ряд (1), а вме­сте с ним и ряд 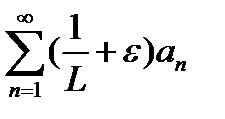, то по теореме 1 сходился бы и ряд (2). А это не так. Значит, ряд (1) также расходится.}

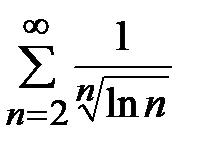. Так как 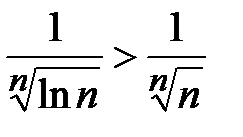, а ряд 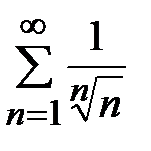- расходится ( 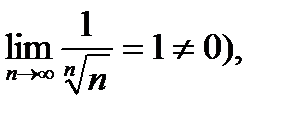то расхо­дится и ряд .

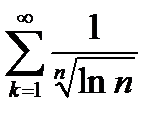Признак Коши и Даламбера

Теорема (признак Коши в предельной форме):Если существует 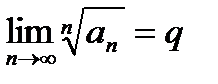, то при 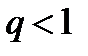ряд (1) сходится; при 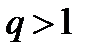расходится, при 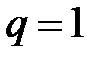этот признак не даёт возможности судить о поведении ряда.

{

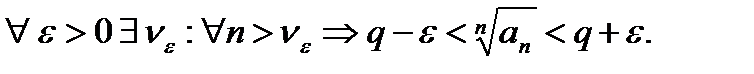
a) 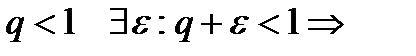начиная с некоторого номера 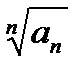< 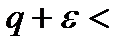1. Ряд схо­дится.

б) 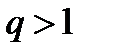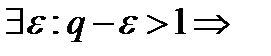начиная с некоторого номера 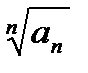>1 . Ряд расходится. }

Теорема (признак Даламбера):Пусть 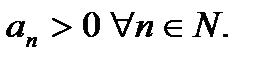Если, начиная с некото­рого номера 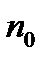, 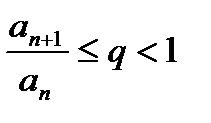для всех 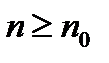, то ряд (1) сходится. Если же 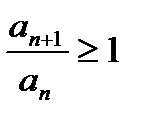, то ряд (1) расходится. { Пусть 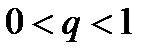. Для 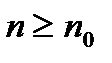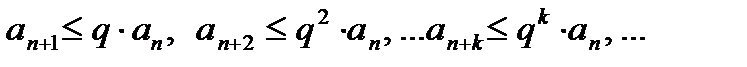Т.к. ряд 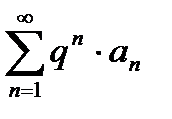- сходится, то, по признаку сравнения, сходится и остаток ряда 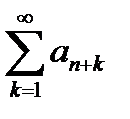, а значит, сходится ряд 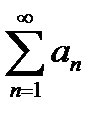(1). Пусть для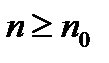 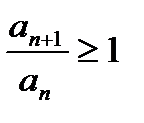. Т.е. 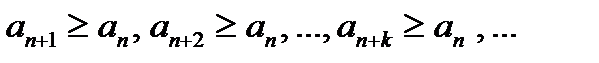и 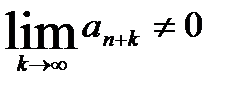, не выполня­ется необходимое условие сходимости ряда. Ряд расходится. }

Теорема (признак Даламбера в предельной форме) :Если 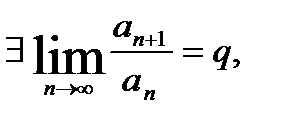то при 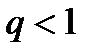ряд (1) сходится, при 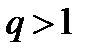расходится, при 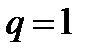этот признак не даёт возможности судить о поведении ряда.

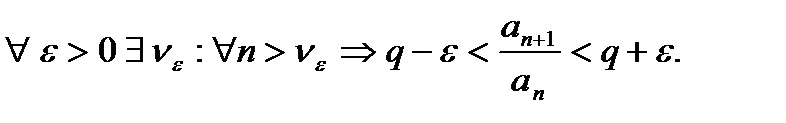{ a) 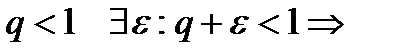начиная с некоторого номера 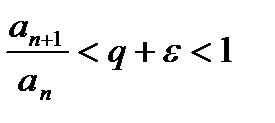Ряд сх.

б) 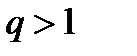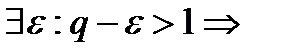начиная с некоторого номера 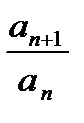>1. Ряд расх. }

5.Интегральный признак сходимости (Признак Коши - Макло­рена)

Теорема (Коши - Маклорена):Пусть функция у = f(x) определена при х≥1, неотрицательна и монотонно убывает на 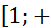∞). Тогда ряд 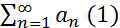, где 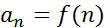сходится тогда и только тогда, ко­гда сходится несобственный интеграл 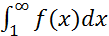(2)

[Так как f(x) монотонна на 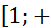∞) , то она интегрируема по Риману на любом отрезке [1, 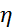], поэтому имеет смысл 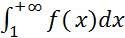. Так как f(x)-убы­вает на 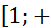∞), то для 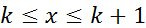f(k+1) 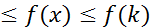. Проинте­грируем последнее неравенство по отрезку 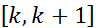: 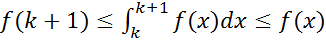, k=1,2,3.4...

Просуммируем по к:

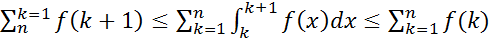Обозначим , 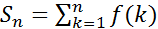Тогда

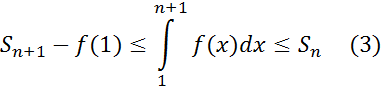
Пусть несобственный интеграл (2) сходится. Последователь­ность 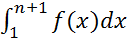монотонна ( 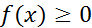) и ограничена. Тогда огра­ничена и после­довательность 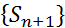. А поскольку она моно­тонно возрастает, то явля­ется сходящейся.

Пусть сходится ряд (1). Покажем, что сходится несобственный инте­грал (2). Последовательность 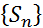– монотонная, сходящаяся последователь­ность, следовательно, ограничена.

Тогда из (3) следует ограниченность возрастающей последова­тельно­сти 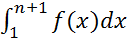, а следовательно, её сходимость. То есть су­ществует конеч­ный 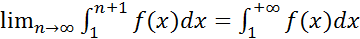; интеграл (2) сходится.}

Пример : 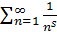, s>0, Рассмотрим f(x)= 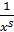на [1, );

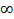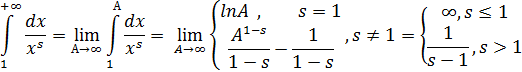
Значит, ряд сходится при s>1 и расходится при s