Критерий Коши сходимости последовательности

Пусть задана последовательность действительных чисел {x_n}, сходящаяся к конечному пределу а: 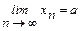, т.е: ("e>0)($kÎN):"n>k ®|x_n-a|<e/2.

Наряду с натуральным числом n>k в неравенство можно подставить и другое mÎN: m>k. Тогда : .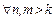

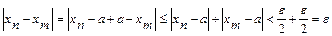Тем самым доказано утверждение:

Если последовательность {x_n} имеет предел, то для неё выполняется условие Коши:

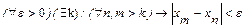. (1)

Последовательность чисел, удовлетворяющая условию Коши (1), называется фундаментальной последовательностью. Справедливо и обратное утверждение.

Теорема (критерий Коши). Для того, чтобы последовательность {x_n} сходилась, необходимо и достаточно, чтобы она была фундаментальной.

По теореме Больцано-Вейерштрасса у всякой ограниченной последовательности существует сходящаяся подпоследовательность { 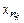}. Пусть 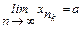. (3)

Докажем, что а является пределом исходной последовательности. Из определения предела (3):

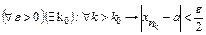. (4)

последовательность по условию фундаментальна, поэтому 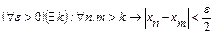.(5)

Пусть N=max(k, k₀). Фиксируем в (4) номер n_K>N (такой номер найдётся, так как n_K®¥ при k®¥). Тогда при m=n_K и при всех n>N в силу (5) выполняется неравенство: 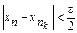. (6)

Неравенства (4), (6) выполняются одновременно при всех n>N. Поэтому

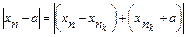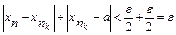£ , т.е. |x_n-a|<e ("n>N). Это означает что .

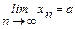1.8. Число е как предел последовательности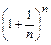

1. Методом математической индукции докажем неравенство Бернулли: ("х>-1)("nÎN)®(1+x)ⁿ³1+nx. (1)

Неравенство (1) справедливо при n=1.

Пусть при n=k неравенство (1) выполняется, т.е.

(1+x)^k³1+kx. (2)

Докажем справедливость (1) при n=k+1. Умножим обе части неравенства (2) на (1+х)>0:

(1+x)^k+1³(1+kx)(1+х) = 1+(1+k)x+kx²³ 1+(1+k)x.

Из последнего, по принципу математической индукции, неравенство Бернулли доказывается для любого nÎN.

2. Пусть 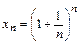, 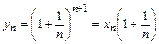. Докажем, что последовательность {y_n} монотонно убывает и ограничена снизу. Оценим отношение:

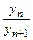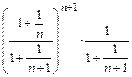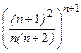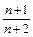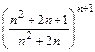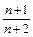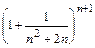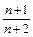= = × = × = × ³

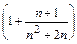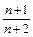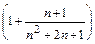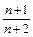³ × > × =1.

Значит, ("nÎN)® y_n+1 < y_n, т.е. {y_n}монотонно убывает.

Учитывая неравенство Бернулли (1), имеем: 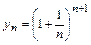³ 1+(n+1) 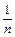=2+ 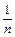> 2 ("nÎN),

т.е. {y_n} ограничена снизу.

3. По теореме о пределе монотонной, ограниченной последовательности можно установить наличие предела для {у_n}, т.е. 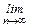у_n=е. Значение предела нам пока неизвестно, но 2<e<3.

4. В произведении 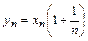, предел которого известен, существует предел второго сомножителя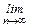 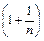=1. Поэтому можно установить и предел первого сомножителя: 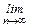x_n=е.

Число е является иррациональным и трансцендентным, т.е. нет алгебраического уравнения с целыми коэффициентами, корнем которого было это число. Его значение мы установим во второй главе.