Определение перемещений в статически неопределимых системах

Известно, что перемещение в любых системах определяется перемножением грузовой эпюры на единичную.

В С.Н.С. для определенных перемещений, очевидно, нужно дважды раскрывать статическую неопределимость. Первый раз — для построения окончательной эпюры от заданных сил, второй раз — для построения эпюры от единичной силы. Однако второй раз раскрывать неопределимость не нужно. Пусть в С.Н.С. нужно найти горизонтальное перемещение точки А (рис. 7.10).

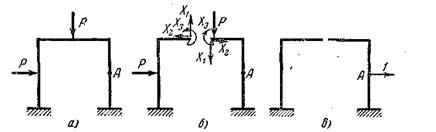
Рис. 7.10

Раскрывая статическую неопределимость, строим окончательную эпюру.

Рассмотрим эквивалентную систему (рис. 7.10,б) после того как найдены неизвестные 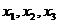, она ничем не отличается от заданной. Если находить перемещения в эквивалентной системе, то 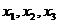войдут в разряд заданных сил и при определении перемещений они также отбрасываются. Поэтому единичную силу 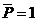нужно прикладывать к основной системе (рис. 7.10,в).

Таким образом, чтобы найти перемещение в С.Н.С. нужно:

1. Раскрыть статическую неопределимость и построить окончательную эпюру.

2. К основной системе приложить единичную силу и построить эпюру.

3. Перемножить две эти эпюры.

Глава 8. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ

Основные понятия

Ранее Вы познакомились с расчетами сооружений и их элементов на прочность и жесткость. Однако для суждения надежности конструкции перечисленных расчетов недостаточно, необходимо сжатые элементы на устойчивость. Что же такое устойчивость?

Устойчивость — это старое русское слово. В знаменитом толковом словаре Даля, опубликованного свыше 100 лет назад, слово “устойчивый” означает “стойкий, крепкий, твердый, не шаткий”. В современных словарях оно определяется как “не поддающийся, не подверженный колебаниям и изменениям”.

Понятие устойчивости встречается во всех областях науки и техники. Достаточно назвать устойчивость движения планет, ракет, самолетов, поездов; устойчивость течения воды в реке; устойчивость горения; устойчивость биологического вида, клетки; устойчивость равновесия телебашни, заводской трубы, высотного здания и т.д. Ясно, что в жизни на движущиеся или покоящиеся тела всегда действуют, не учтенные расчетом, малые возмущения, стремящиеся вывести их из этих состояний.

Если малые возмущения вызывают малые отклонения системы от невозмущенного состояния, то невозмущенное состояние является устойчивым.

Таким образом, малые возмущения являются причиной, выводящей систему от невозмущенного состояния. Следствием является ее возврат к первоначальному, либо отклонение от него. И причина и следствие не имеют общей меры и оцениваются в зависимости от обстоятельств.

Пусть имеем многоэтажные здания — близнецы в Москве и Ашхабаде. Поскольку в Москве землетрясений не бывает, то нет опасения за его устойчивость. В сейсмическом районе Ашхабада это здание уже нельзя считать устойчивым, причем одному человеку оно может казаться устойчивым, другому неустойчивым. Для количественного анализа такая оценка совершенно неприемлема. Она нуждается в точном определении, чтобы явление было переложено на язык математического анализа.

Прежде всего, возникает вопрос, что при анализе устойчивости конструкции можно не принимать во внимание и что необходимо учитывать? Короче говоря, как выбрать расчетную схему?

Выбор расчетной схемы зависит от определения понятия устойчивости. Решение большинства задач упругой устойчивости основано на двух простейших понятиях устойчивости Эйлера и Лагранжа. При этом вводятся следующие предпосылки:

1). Геометрическая и силовая схема принимается идеальными (т.е. стержень идеально прямой и идеально упругий, нагрузки приложены в ц.т. сечения).

2). Возмущения, которые налагаются на систему, являются сколь угодно малыми.

Определение устойчивости по Эйлеру:

Равновесие стержня, находящегося под действием продольной силы 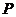, устойчиво по Эйлеру, если после статического приложения и статического снятия возмущающей силы 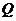, он возвращается к первоначальному положению равновесия.

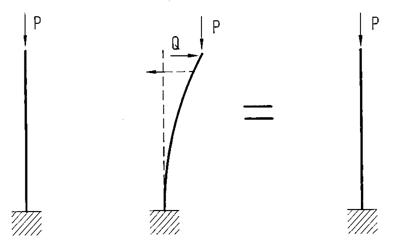
Рис. 8.1

Равновесие стержня, находящегося под действием продольной силы 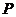, устойчиво по Лагранжу, если после статического приложения возмущающей силы 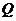и мгновенно ее снятие, стержень после колебаний возвратится к первоначальному положению равновесия.

В математическом смысле понятия устойчивости по Эйлеру — Лагранжу сводится к отысканию нагрузки, при которой происходит бифуркация форм равновесия. Нагрузка, при которой происходит разветвление форм равновесия, называется критической.

При расчете конструкций критическая нагрузка принимается за предельную, по которой и назначается запас устойчивости. Величина запаса устойчивости зависит от условий эксплуатации, а также от степени ответственности конструкции.

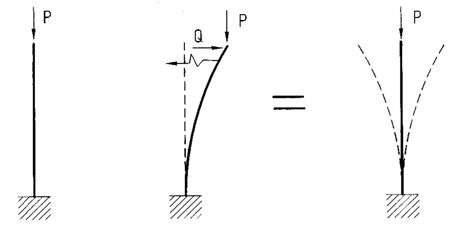
Рис. 8.2