Зависимость между моментами инерции сечения при повороте осей. Главные оси и главные моменты инерции

Пусть заданы моменты инерции 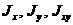. Требуется найти 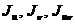, относительно осей, повернутых к заданным на угол 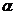(рис. 4.5).

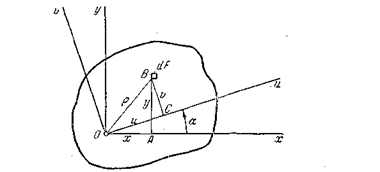
Рис. 4.5

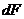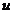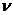Выберем произвольную площадку и выразим ее координаты в новых осях и через старые .

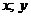Проектируем замкнутый четырехугольник 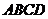на ос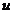и и 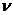. Так как проекция ломаной линии равна проекции замыкающей, находим:

.

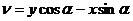
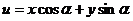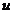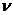
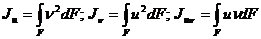В выражениях исключаем и тогда

,

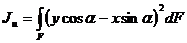
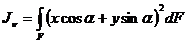
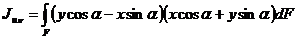откуда

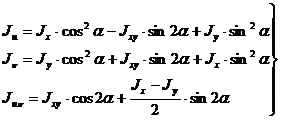(4.5)

Рассмотрим первые два уравнения из 4.5, складывая их почленно, получим:

.

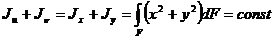Таким образом, при повороте осей сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной. Заметим, что 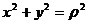, где 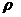— расстояние от элементарной площадки до точки 0.

Таким образом

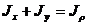, (4.6)

где 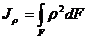— полярный момент инерции.

При помощи выражения 4.6 легко найти осевые моменты инерции для круга.

.

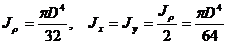С изменением 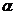каждая из величин 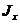и 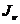меняется, а сумма их остается постоянной. Следовательно, существует такой угол 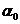, при котором один из элементов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.

Дифференцируя первое выражение из 4.5 по 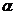, и приравнивая производную нулю, найдем

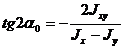(4.7)

При этом значение 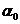один из осевых моментов достигает максимального значения, другой - минимального, а центробежный равен 0.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями.

Найдем величины главных моментов инерции. Для этого первые две формулы из 4.5 приведем к виду

.

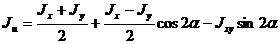
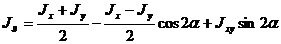Учитывая, что

,

.

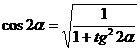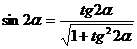Исключаем при помощи 4.7 угол 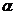, получим для определения значений главных моментов инерции.

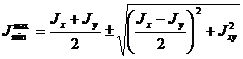. (4.8)

Глава 5. ИЗГИБ

Основные понятия

Под изгибом понимается такой вид нагружения стержня, когда в его поперечных сечениях возникают изгибающие моменты. Если изгибающий момент является единственным силовым фактором, то изгиб называется чистым. Большей частью в поперечных сечениях бруса наряду с изгибающими моментами возникают и поперечные силы. В этом случае изгиб называют поперечным. В дальнейшем встретимся с более сложными видами изгиба.

Брус, работающий на изгиб, обычно называют балкой. Кроме балок на изгиб работают элементы рам. Рамой называется конструкция, состоящая из стержней, элементы которой работают преимущественно на изгиб.

Ранее мы уже познакомились с внутренними силовыми факторами 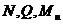, возникающими при изгибе, и строили их эпюры. Теперь перейдем к исследованию напряжений, возникающих при изгибе.

5.2. Дифференциальные зависимости между 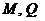и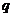

Изгибающий момент 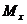, поперечная сила 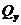и интенсивность внешней нагрузки 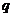связаны между собой определенной зависимостью. Вырежем из балки, загруженной распределенной нагрузкой 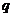, изменяющейся по какому—либо закону (рис. 5.1,а), элемент длиной 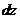(рис. 5.1,б).

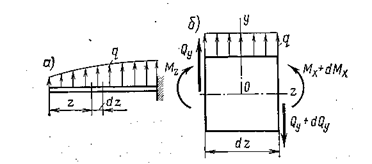
Рис. 5.1

Нагрузку считают положительной, если она направлена вверх; на протяжении длины 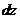ее считают равномерно распределенной.

Составим два уравнения равновесия элемента:

.

.

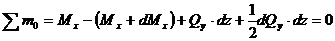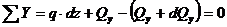В первом уравнении произведением 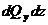как величиной второго порядка малости по сравнению с остальными слагаемыми можно пренебречь.

После элементарных преобразований из приведенных выше уравнений находим

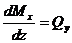. (5.1)

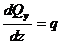. (5.2)

Из двух полученных дифференциальных зависимостей вытекает третья:

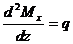. (5.3)

Зависимости (5.1) и (5.2) часто используются при проверке правильности построения эпюр моментов и поперечных сил.