Положение мгновенного центра ускорений и мгновенного центра скоростей в общем случае в любой данный момент времени не совпадают.
Сферическое движение твердого тела. Эйлеровы углы. Уравнения сферического движения.
Сферическим движением (движением тела с одной закрепленной точкой) называется такое движение тела, при котором одна его точка О остается неподвижной во все время движения. Все остальные точки тела движутся при этом по траекториям, расположенным на поверхности сфер с центром в неподвижной точке О. Положение тела определяется углами Эйлера (рис. 1): углом прецессии φ, углом нутации θ и углом собственного вращения φ. Эти углы характеризуют положение координатного трехгранника осей Oξηζ, связанного с телом, по отношению к неподвижному трехграннику Oxyz. Линия ON пересечения координатных плоскостей Оху и Oξη называется линией узлов.
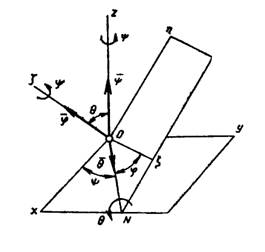
Рисунок 1.
Уравнения сферического движения:
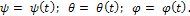
РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ. Во всякий момент времени существует проходящая через неподвижную точку О прямая OΩ, скорости точек которой равны нулю. Это мгновенная ось вращения. Мгновенная угловая скорость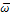 
определяется соотношением
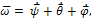
где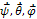 
- векторы, численно равные производным углов Эйлера и направленные соответственно по осям z, ON и ζ. Мгновенная угловая скорость может менять свое положение в пространстве, описывая коническую поверхность, поэтому вектор углового ускорения
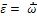
в общем случае не совпадает по направлению с 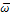(рис. 2).
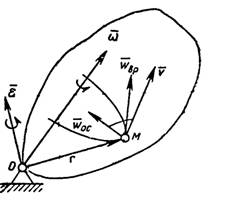
Рисунок 2.
Скорость точки при сферическом движении тела
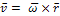
или в аналитической форме (формулы Эйлера):
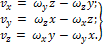
Ускорение точки складывается из осестремительной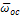 
и вращательной 
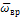составляющих (рис. 2):
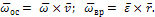
Теорема Эйлера Даламбера
Теорема Эйлера-Даламбера: всякое перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом вокруг некоторой мгновенной оси вращения, проходящей через эту точку. Скорости всех точек тела, лежащих на мгновенной оси вращения в данный момент времени равны нулю. Вектор угловой скорости (мгновенной угловой скорости) откладывается о неподвижной точки по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение происходящим против час.стр. Вектор угловой скорости со временем изменяется не только по численной величине, но и по направлению. Конец вектора описывает годограф скорости вектора . Угловое ускорение: – скорость конца вектора , совпадает по направлению с касательной к годографу вектора угловой скорости. В случае сферич. движение в отличии от случая вращения вокруг неподвижной оси вектор не совпадает с направлением . Скорости точек при сферич. движ.: – векторное произведение, – радиус-вектор точки, проведенный из неподвижной точки, модуль v=rsin=h, h– расстояние от точки до мгновенной оси вращения. Формулы Эйлера: .
МГНОВЕННАЯ ОСЬ ВРАЩЕНИЯ
прямая, неподвижная в данный момент в нек-рой инерциальнойсистеме отсчёта, относительно к-рой сложное движение твёрдого тела в этот момент можно представить каквращат. вокруг этой прямой. М. о. в. может лежать как внутри тела, так и вне его. С течением времениположение М. о. в. изменяется относительно как неподвижной системы отсчёта, так и системы отсчёта,движущейся вместе с телом.