Взаимное расположение точки, прямых и плоскостей

Взаимное расположение точки и прямой

Возможны два варианта расположения точки относительно прямой:

1) точка принадлежит прямой (рис. 3.1 а), тогда, согласно основным свойствам прямоугольного проецирования[4], на КЧ ее проекции лежат на одноименных проекциях прямой.

;

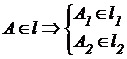2) точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой.

; .

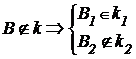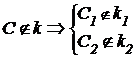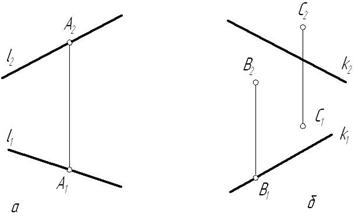
Рис. 3.1

Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

2) пересекаться;

3) скрещиваться.

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

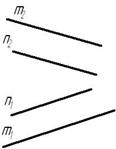
Рис. 3.2

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

.

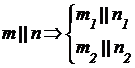Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная ( 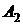) и горизонтальная ( 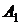)проекции этой точки должны находиться на одной линии связи.

.

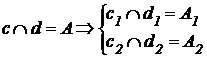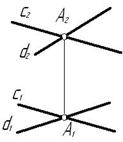
Рис. 3.3

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

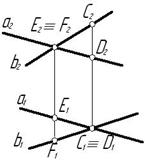
Рис. 3.4

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

Принадлежность прямой и точки плоскости

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

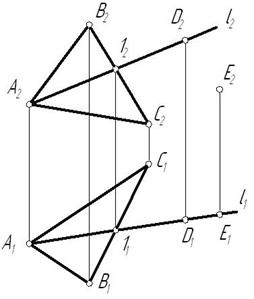
Рис. 3.5

На рис. 3.5 изображена плоскость 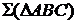и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

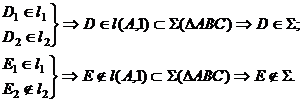
На рис. 3.6 показана плоскость 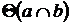и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.

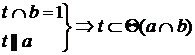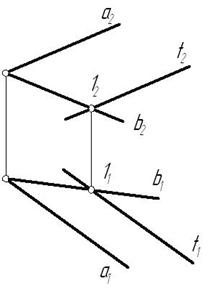
Рис. 3.6

Линии уровня плоскости

Линиями уровня плоскости называются прямые, лежащие в плоскости и параллельные одной из плоскостей проекций.

Существуют три линии уровня плоскости: горизонталь плоскости, фронталь плоскости и профильная прямая плоскости.

1. Горизонталь плоскости – прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.

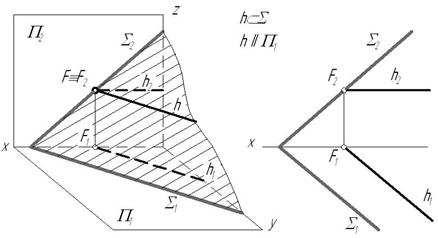
Рис. 3.7

Признаки и свойства горизонтали плоскости:

1) все горизонтали плоскости параллельны друг другу;

2) фронтальный след горизонтали (точка F) принадлежит фронтальному следу плоскости;

3) горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

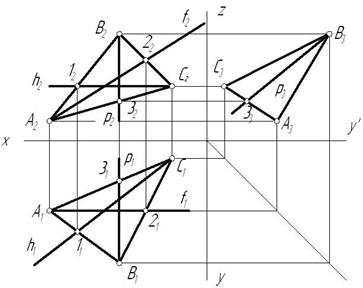
Рис. 3.8

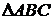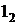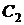На рис. 3.8 приведена плоскость общего положения, заданная ,и принадлежащая ей горизонталь h. Если плоскость не задана следами, то построение горизонтали плоскости начинают с построения ее фронтальной проекции, идущей параллельно оси х. Т.к. горизонталь принадлежит плоскости, то она имеет с ней две общие точки – 1 и С. Зная их фронтальные проекции и , по линиям связи можно получить горизонтальные проекци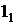и и 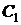,а затем, соединив между собой, получить горизонтальную проекцию горизонтали.

2. Фронталь плоскости – прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.

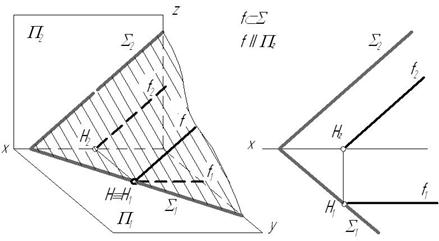
Рис. 3.9

Признаки и свойства фронтали плоскости:

1) все фронтали плоскости параллельны друг другу;

2) горизонтальный след фронтали (точка H) принадлежит горизонтальному следу плоскости;

3) фронтальная проекция фронтали параллельна фронтальному следу плоскости.

Если плоскость не задана следами, то построение фронтали плоскости начинают с построения ее горизонтальной проекции, идущей параллельно оси х (рис. 3.8). Т.к. фронталь принадлежит плоскости, то имеет с ней две общие точки – 2 и А. Имея их горизонтальные проекци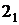и и 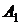, по линиям связи можно получить фронтальные проекции 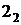и ,а затем, соединив между собой, получить фронтальную проекцию фронтали.

3. Профильная прямая плоскости – прямая лежащая в плоскости и параллельная профильной плоскости проекций (рис. 3.10).

Признаки и свойства профильной прямой плоскости:

1) все профильные прямые плоскости параллельны друг другу;

2) фронтальный след профильной прямой (точка F) принадлежит фронтальному следу плоскости, а ее горизонтальный след (точка H) – горизонтальному следу плоскости;

3) профильная проекция профильной прямой параллельна профильному следу плоскости.

Если плоскость не задана следами, то построение профильной прямой плоскости начинают с построения ее фронтальной или горизонтальной проекций, идущих перпендикулярно оси х (рис. 3.10).

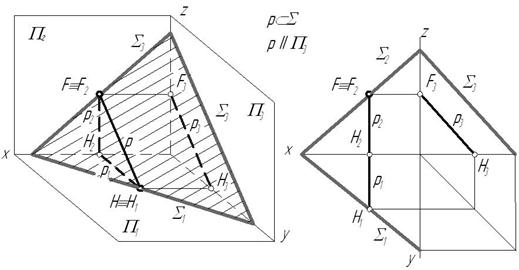
Рис. 3.10