Положение прямой относительно плоскостей проекций

По расположению относительно плоскостей проекций различают прямые общего и частного положения.

Прямые не параллельные и не перпендикулярные ни одной из плоскостей проекций называются прямыми общего положения.

Признаки и свойства прямой общего положения:

1) На КЧ ни одна из проекций прямой общего положения, не параллельна осям проекций (или не перпендикулярна линиям связи) (рис. 2.5, 2.6).

2) Длина отрезка, принадлежащего прямой общего положения проецируется на любую плоскость проекций с искажением: каждая проекция отрезка короче его натуральной величины.

Прямые общего положения могут быть восходящими или нисходящими.

Прямая называется восходящей, если по мере удаления от наблюдателя она повышается.

Прямая называется нисходящей, если по мере удаления от наблюдателя она понижается.

Для того, чтобы определить по КЧ положение прямой, необходимо обратить внимание на то, как дальняя от наблюдателя точка отрезка прямой расположена относительно ближайшей точки: выше или ниже, правее или левее. На рисунке 2.5 изображена восходящая вправо прямая, т.к. наиболее удаленная точка В располагается правее и выше ближайшей точки А.

Признак восходящих и нисходящих прямых:

1) На КЧ горизонтальная и фронтальная проекции имеют уклон в одну сторону относительно оси проекций (рис. 2.7 – прямая l).

2) У нисходящих прямых обе проекции наклонены в разные стороны относительно оси проекций (рис. 2.7 – прямая k).

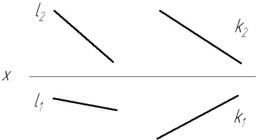
Рис. 2.7

Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Прямые, параллельные одной из плоскостей проекций, называются прямыми уровня.

Существует три вида прямых уровня: горизонталь, фронталь и профильная прямая.

1. Горизонталь(h)– прямая, параллельная горизонтальной плоскости проекций.

Признаки и свойства горизонтали:

1) На КЧ фронтальная проекция горизонтали 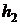располагается параллельно оси 0х (или в безосном чертеже перпендикулярно линиям связи).

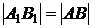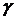2) На горизонтальную плоскость проекций без искажения проецируются отрезок, принадлежащий горизонтали ( ), и углы наклона его к фронтальной ( ) и профильной ( ) плоскостям проекций.

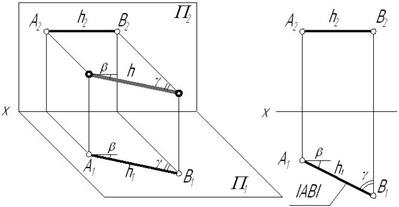
Рис. 2.8

2. Фронталь(f) – прямая, параллельная фронтальной плоскости проекций.

Рис. 2.9

Признаки и свойства фронтали:

1) На КЧ горизонтальная проекция фронтали располагается параллельно оси 0х (или в безосном чертеже перпендикулярно линиям связи).

2) На фронтальную плоскость проекций проецируются без искажения отрезок, принадлежащий фронтали ( 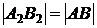), и углы наклона его к горизонтальной ( 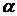) и профильной ( 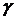) плоскостям проекций.

3. Профильная прямая – прямая, параллельная профильной плоскости проекций.

Признаки и свойства профильной прямой:

1) На КЧ фронтальная 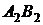и горизонтальная 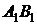проекции отрезка профильной прямой располагаются перпендикулярно оси х.

2) На профильную плоскость проекций проецируются без искажения отрезок, принадлежащий профильной прямой ( 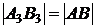), и углы наклона его к фронтальной ( 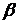) и горизонтальной ( 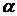) плоскостям проекций.

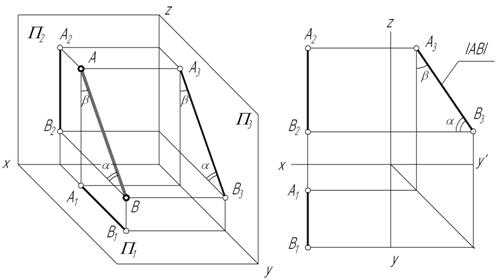
Рис. 2.10

Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими прямыми.

Существует три вида проецирующих прямых: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая прямая.

Проекцией проецирующей прямой на плоскость проекций, к которой она перпендикулярна, является точка (след прямой). Все точки, принадлежащие проецирующей прямой, проецируются на ее след.

1. Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций.

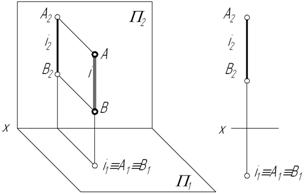Рис. 2.11

2.Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций.

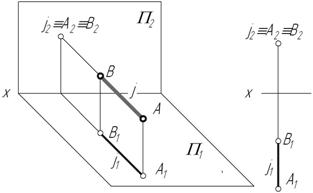
Рис. 2.12

3. Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций.

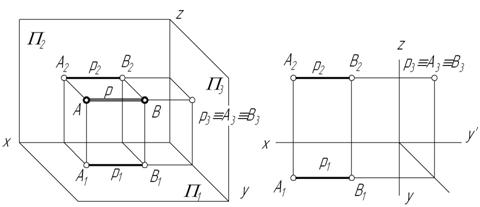
Рис. 2.13

К числу частных случаев расположения прямых можно отнести и прямые, лежащие непосредственно в плоскостях проекций. Их называют прямыми нулевого уровня. На рис. 2.14 приведены примеры таких прямых: горизонталь h и профильно-проецирующая прямая j располагаются на горизонтальной плоскости проекций, следовательно их фронтальные проекции находятся на оси 0х; фронталь f и профильно-проецирующая прямая р лежат во фронтальной плоскости проекций, а значит их горизонтальные проекции на КЧ совпадают с осью 0х.

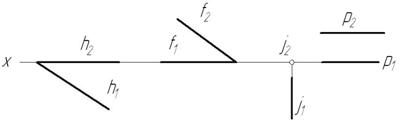
Рис. 2.14

Следы прямых линий

Точка пересечения прямой с плоскостью проекций называется следом прямой.

На рисунке 2.7 приведены пространственная модель и КЧ прямой l, пересекающей три плоскости проекций, а следовательно, имеющей три следа:

- горизонтальный ,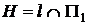

- фронтальный ,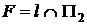

- профильный след .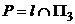

Очевидно, что фронтальная и профильная проекции горизонтального следа (H) прямой лежат на осях проекций 0х и 0y соответственно. Проекции фронтального (F) и профильного (P) следов прямой находятся аналогично.

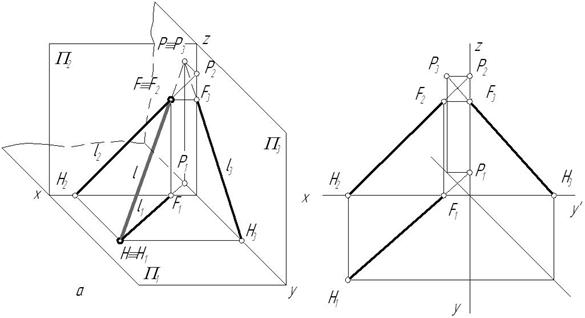
Рис. 2.15

Прямые общего положения пересекают три плоскости проекции и имеют три следа; прямые уровня пересекают две плоскости проекций (имеют два следа); проецирующие прямые пересекают одну плоскость проекции.