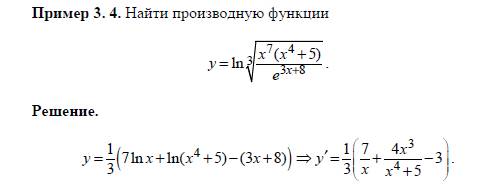Формулы для производных произведения, частного, сложной функции, функции, заданной параметрически, неявной функции.
ВОПРОСЫ
1. Формулы для производных произведения, частного, сложной функции, функции, заданной параметрически, неявной функции.
2. Действия над матрицами, вычисление обратной матрицы, решение простейших матричных уравнений, жордановы исключения.
3. Постановка задачи межотраслевого баланса (модель В.Леонтьева). Векторы объемов конечной и валовой продукции. Матрица коэффициентов прямых затрат.
4. Решение уравнений межотраслевого баланса матричным способом. Матрица коэффициентов полных затрат.
5. Общее решение однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Постановка задачи Коши.
6. Классическое определение вероятности. Геометрические вероятности. Операции над событиями. Вероятность суммы двух событий.
7. Условная вероятность. Независимость двух событий.
8. Формула полной вероятности. Формула Байеса.
9. Последовательность независимых испытаний Бернулли. Формула Бернулли для числа «успехов».
10. Понятие о дискретной случайной величине. Закон распределения, математическое ожидание, дисперсия и их свойства.
11. Важнейшие виды распределений дискретных случайных величин (геометрическое, биномиальное, Пуассона) и их характеристики.
12. Понятие о непрерывной случайной величине. Функция распределения, плотность, математическое ожидание, дисперсия и их свойства.
13. Важнейшие виды распределений непрерывных случайных величин (равномерное, показательное, нормальное) и их характеристики.
14. Группировка выборочных данных одномерной выборки, интервальный и дискретный вариационный ряд, гистограмма и полигон относительных частот.
15. Оценки для характеристик случайных величин. Среднее выборочное значение, выборочная дисперсия, среднее выборочное квадратическое отклонение. Несмещенные оценки.
16. Ковариация и коэффициент корреляции двух случайных величин. Корреляционная таблица для двумерной выборки.
17. Постановка основной задачи линейного программирования. Построение двойственной задачи к задаче линейного программирования. Экономический смысл двойственной задачи.
18. Симплекс–метод решения основной задачи линейного программирования.
19. Графический метод решения задач линейного программирования в случае двух переменных.
20. Постановка транспортной задачи. Построение первоначального плана перевозок с помощью методов северо-западного угла и наименьшей стоимости.
21. Решение транспортной задачи методом потенциалов.
22. Принцип минимакса для матричных игр.
23. Определение решения игры для матричных игр в случае неоднократного повторения игры. Смешанные стратегии.
24. Аналитический метод решения матричных игр типа 2´2.
25. Графический метод решения матричных игр типа 2´ nи типа m ´2.
26. Сетевой график производства работ. Критическое время завершения процесса работ. Некритические операции
27. Кратчайший путь из источника в сток в сети.
28. Предоставление ссуд на срок в 1 год на основе годовых процентных и учетных ставок.
29. Предоставление ссуд на срок, выражаемый в годах, по схемам простых и сложных процентов на основе процентной ставки.
30. Уравнение регрессии и его построение
31. Способы определения срока возврата ссуды в годах для ссуд, выданных на срок, исчисляемый в днях (английский, французский и немецкий способы).
32. Наращение по схемам простых и сложных процентов в случае плавающих процентных ставок.
33. Сравнение денежных сумм, выплаченных в различные моменты времени.
34. Конечные и бесконечные финансовые ренты.
35. Современная величина ренты.
36. Потребительский кредит.
37. Ломбардный кредит.
38. Операция учета векселей.
ОТВЕТЫ
Производные функций
Производные суммы, разности, произведения, частного, степени:
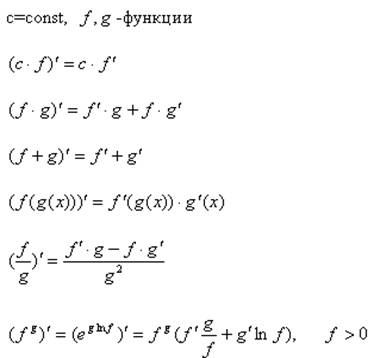
Пояснение к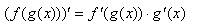 
- сложная функция.
Если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то ,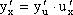 
или 
.
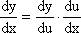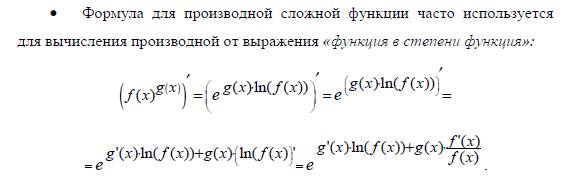
Производные степенных функций:
Производные показательных функций:
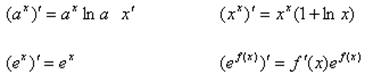
Производные логарифмических функций:
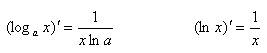
Производные тригонометрических функций:
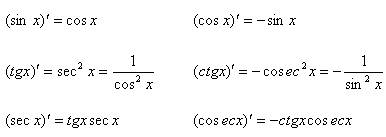
Производные обратных тригонометрических функций:
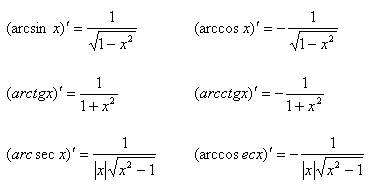
Производная функции заданной параметрически:
Пусть задана зависимость двух переменных x и y от параметра t, изменяющегося в пределах от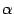 
до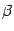 
: 
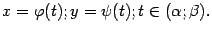
Пусть функция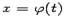 
имеет обратную: 
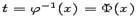. Тогда мы можем, взяв композицию функци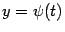й 
и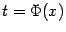 
, получить зависимость y от x: 
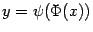. Зависимость величины y от величины x, заданная через зависимость каждой из них от параметра t в виде 
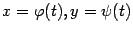, называется функцией 
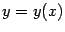, заданной параметрически.
Производную функции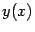 
, заданной параметрически, можно выразить через производные функци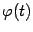й 
и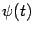 
: поскольку 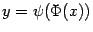и, по формуле производной обратной функции, 
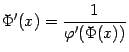, то
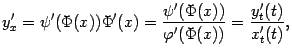
где 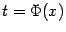- значение параметра, при котором получается интересующее нас при вычислении производной значение .
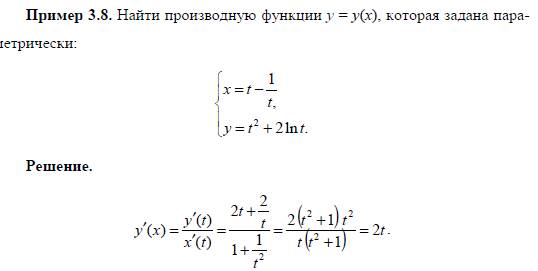
Производная неявной функции:
Если функция y=y(x) задана неявно уравнением F(x,y)=0 , F(x,y) — дифференцируемая функция и F 'y( x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = - F'x(x, y) / F'y(x, y).
или
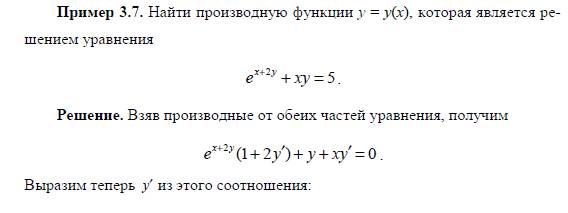
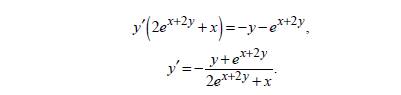
ПРИМЕРЫ:
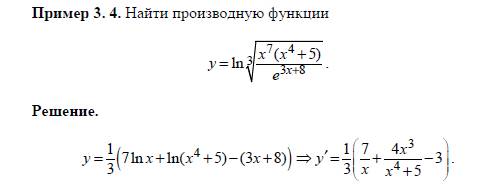
Постановка задачи Коши.
Определение. Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданному начальному условию, называется задачей Коши.
Из всех разделов математического анализа, дифференциальные уравнения являются одним из самых важных по своим приложениям, ибо решая дифференциальное уравнение, т.е. находя некоторую функцию, мы устанавливаем закон, по которому происходит то или иное явление или процесс.
Определение. Решить задачу Коши для уравнения y'=f(x,y) (6.1) – это значит найти решение уравнения y'=f(x,y) в виде функции у(х), удовлетворяющей начальному условию у(х0)=у0. Геометрически это означает, что требуется найти интегральную кривую у=у(х), проходящую через заданную точку M0(x0,y0) при выполнении равенства (6.1).
Операции над событиями.
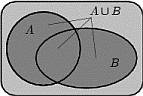
1. Объединением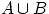 
(или суммой A+B) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С.
Объединением событий A и B называется событие, состоящее в том, что произошло либо A, либо B, либо оба события одновременно.
2. Совмещением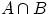 
(или произведением A*B) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.
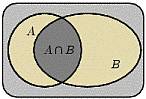
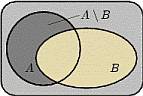
3. Разностью (дополнение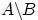 
) событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.
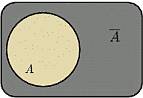
4. Противоположным к событию A называется событие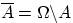 
, состоящее в том, что событие A в результате эксперимента не произошло. Т.е. множество 
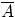состоит из элементарных исходов, не входящих в A.
5. События A и B называют несовместными, если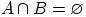 
, т.е. совмещение (произведение) А и В равно пустому множеству (нулю), они не могут произойти одновременно.
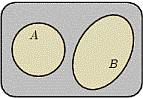
Биномиальное распределение.
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, распределение Бернулли, - распределение вероятностей случайной величины X, принимающей целочисленные значения х = 0, 1, ..., n с вероятностями соответственно.
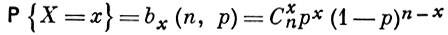
(Сxn - биномиальный коэффициент; р - параметр Б. р., наз. вероятностью положительного исхода, принимающей значения на отрезке 0 ≤ р ≤ 1). Б. р. - одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Пусть Y1, Y2,... - последовательность независимых случайных величин, каждая из к-рых может принимать лишь два значения 1 или 0 с вероятностями р и 1 - р соответственно. Величины Yi можно трактовать как результаты независимых испытаний, причем Yi = 1 в случае «положительного исхода» и Yi = 0 в случае «отрицательного исхода» испытания с номером i.
М(Х)=np
D(X)=np(1-p)
Распределение Пуассона.
Дискретная случайная величина X имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, ..., m, ... (бесконечное, но счётное множество значений) с вероятностями
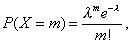где m=0, 1, 2, ...
Ряд распределения закона Пуассона имеет вид:
xi 0 1 2 ... m ...
pi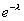 
... 
...
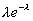
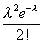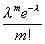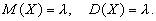
При условии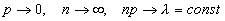 
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Наряду с "предельным" случаем биномиального распределения закон Пуассона может возникнуть и в ряде других случаев. Так для простейшего потока событий число событий, попадающих на произвольный отрезок времени, есть случайная величина, имеющая пуассоновское распределение. Также по закону Пуассона распределены, например, число рождения четверней, число сбоев на автоматической линии, число отказов сложной системы в "нормальном режиме", число "требований на обслуживание", поступивших в единицу времени в системах массового обслуживания, и др.
Метод наименьшей стоимости.
При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них.
Пример:
| Пункты отправления | Пункты назначения | Запасы | |||||||||
 |  |  |  |  | |||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
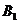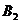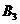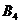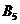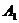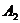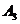| Потребности |
В данном случае заполнение таблицы начинается с клетки для неизвестного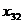 
, для которого мы имеем значение 
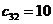, наименьше из всех значений 
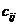. Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе 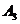и второму заказчику 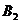. Третья база 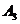может полностью удовлетворить потребность второго заказчика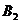 
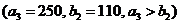. Полагая 
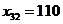, вписываем это значение в клетку 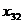и исключаем из рассмотрения второй столбец. На базе 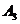остается изменённый запас 
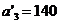. В оставшейся новой таблице с тремя строками 
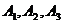и четырьмя столбцами 
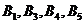клеткой с наименьшим значением 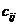клетка, где 
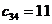. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В результате оказываются заполненными (в приведенной последовательности) следующие клетки:
.
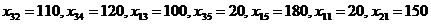На пятом шаге клеток с наименьшими значениями 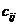оказалось две 
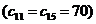. Мы заполнили клетку для 
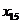, положив 
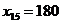. Можно было выбрать для заполнения другую клетку, положив 
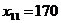, что приведет в результате к другому опорному плану. Общий объем перевозок в тонно-километрах для этого плана составит
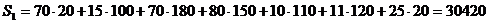
Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами (что и имеет место в нашем примере), хотя это и не обязательно.
Современная величина ренты.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 71
Потребительский кредит.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 47
Ломбардный кредит.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 30
Операция учета векселей.
Самаров- ФИНАНСОВАЯ МАТЕМАТИКА.pdf СТР 73
ИНТЕГРАЛЫ:
- ---------------------------------------------------------------------------------------------------------
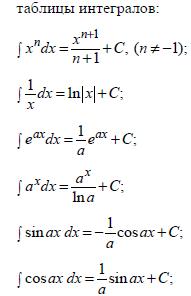
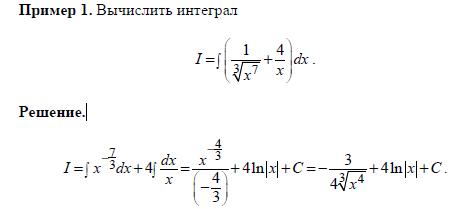
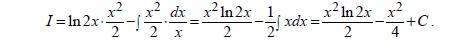
[1] Апатенок Р.Ф. Математика для экономистов. М, Просвещение, 2004. – С. 120
ВОПРОСЫ
1. Формулы для производных произведения, частного, сложной функции, функции, заданной параметрически, неявной функции.
2. Действия над матрицами, вычисление обратной матрицы, решение простейших матричных уравнений, жордановы исключения.
3. Постановка задачи межотраслевого баланса (модель В.Леонтьева). Векторы объемов конечной и валовой продукции. Матрица коэффициентов прямых затрат.
4. Решение уравнений межотраслевого баланса матричным способом. Матрица коэффициентов полных затрат.
5. Общее решение однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Постановка задачи Коши.
6. Классическое определение вероятности. Геометрические вероятности. Операции над событиями. Вероятность суммы двух событий.
7. Условная вероятность. Независимость двух событий.
8. Формула полной вероятности. Формула Байеса.
9. Последовательность независимых испытаний Бернулли. Формула Бернулли для числа «успехов».
10. Понятие о дискретной случайной величине. Закон распределения, математическое ожидание, дисперсия и их свойства.
11. Важнейшие виды распределений дискретных случайных величин (геометрическое, биномиальное, Пуассона) и их характеристики.
12. Понятие о непрерывной случайной величине. Функция распределения, плотность, математическое ожидание, дисперсия и их свойства.
13. Важнейшие виды распределений непрерывных случайных величин (равномерное, показательное, нормальное) и их характеристики.
14. Группировка выборочных данных одномерной выборки, интервальный и дискретный вариационный ряд, гистограмма и полигон относительных частот.
15. Оценки для характеристик случайных величин. Среднее выборочное значение, выборочная дисперсия, среднее выборочное квадратическое отклонение. Несмещенные оценки.
16. Ковариация и коэффициент корреляции двух случайных величин. Корреляционная таблица для двумерной выборки.
17. Постановка основной задачи линейного программирования. Построение двойственной задачи к задаче линейного программирования. Экономический смысл двойственной задачи.
18. Симплекс–метод решения основной задачи линейного программирования.
19. Графический метод решения задач линейного программирования в случае двух переменных.
20. Постановка транспортной задачи. Построение первоначального плана перевозок с помощью методов северо-западного угла и наименьшей стоимости.
21. Решение транспортной задачи методом потенциалов.
22. Принцип минимакса для матричных игр.
23. Определение решения игры для матричных игр в случае неоднократного повторения игры. Смешанные стратегии.
24. Аналитический метод решения матричных игр типа 2´2.
25. Графический метод решения матричных игр типа 2´ nи типа m ´2.
26. Сетевой график производства работ. Критическое время завершения процесса работ. Некритические операции
27. Кратчайший путь из источника в сток в сети.
28. Предоставление ссуд на срок в 1 год на основе годовых процентных и учетных ставок.
29. Предоставление ссуд на срок, выражаемый в годах, по схемам простых и сложных процентов на основе процентной ставки.
30. Уравнение регрессии и его построение
31. Способы определения срока возврата ссуды в годах для ссуд, выданных на срок, исчисляемый в днях (английский, французский и немецкий способы).
32. Наращение по схемам простых и сложных процентов в случае плавающих процентных ставок.
33. Сравнение денежных сумм, выплаченных в различные моменты времени.
34. Конечные и бесконечные финансовые ренты.
35. Современная величина ренты.
36. Потребительский кредит.
37. Ломбардный кредит.
38. Операция учета векселей.
ОТВЕТЫ
Формулы для производных произведения, частного, сложной функции, функции, заданной параметрически, неявной функции.
Определение производной :
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке хo называется предел:
= 
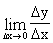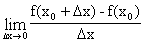
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен ∞ (или -∞ ), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хo бесконечную производную.
Производная обозначается символами:
y ' ; f ' (xo) ;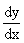 
; 
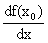
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t0.
Производные функций
Производные суммы, разности, произведения, частного, степени:
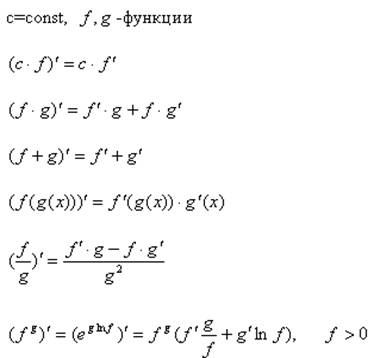
Пояснение к 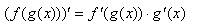- сложная функция.
Если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то , 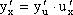или .
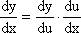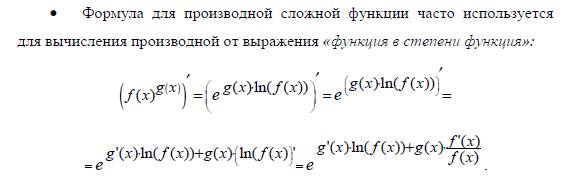
Производные степенных функций:
Производные показательных функций:
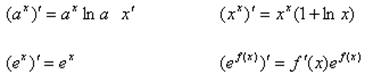
Производные логарифмических функций:
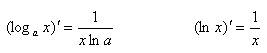
Производные тригонометрических функций:
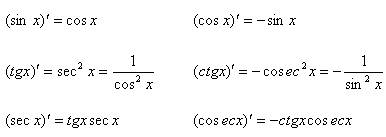
Производные обратных тригонометрических функций:
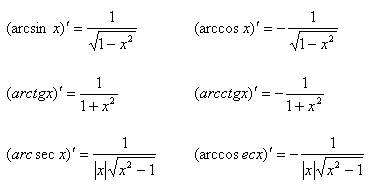
Производная функции заданной параметрически:
Пусть задана зависимость двух переменных x и y от параметра t, изменяющегося в пределах от 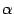до :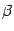
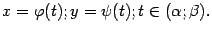
Пусть функция 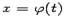имеет обратную: 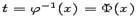. Тогда мы можем, взяв композицию функци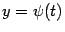й и 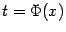, получить зависимость y от x: 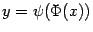. Зависимость величины y от величины x, заданная через зависимость каждой из них от параметра t в виде 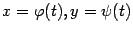, называется функцией 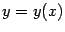, заданной параметрически.
Производную функции 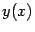, заданной параметрически, можно выразить через производные функци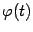й и 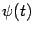: поскольку 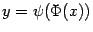и, по формуле производной обратной функции, 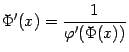, то
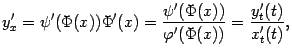
где 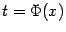- значение параметра, при котором получается интересующее нас при вычислении производной значение .
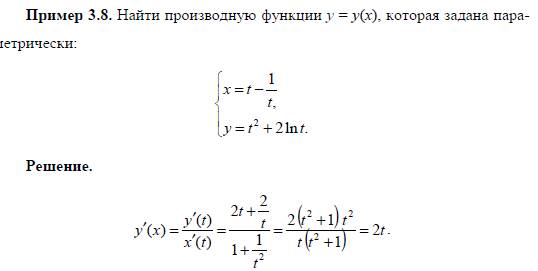
Производная неявной функции:
Если функция y=y(x) задана неявно уравнением F(x,y)=0 , F(x,y) — дифференцируемая функция и F 'y( x, y) не равен 0, то производная y'(x) вычисляется по формуле y'(t) = - F'x(x, y) / F'y(x, y).
или
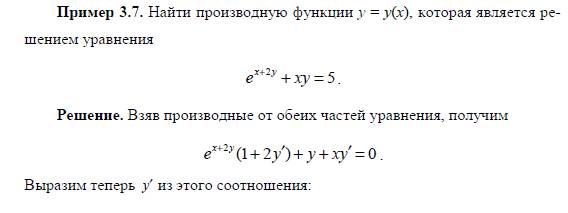
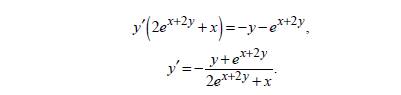
ПРИМЕРЫ: