Билинейные и квадратичные формы.
Классификация квадратичных форм. Теорема об инерции.
Понятие билинейной формы.
Билинейной формой назовем отображение 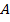 пары векторов
пары векторов 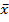 и
и 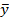 в вещественное число, ктр удовлетворяет следующим условиям: 1).
в вещественное число, ктр удовлетворяет следующим условиям: 1). 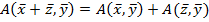 ; 2).
; 2). 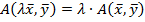 ; 3).
; 3). 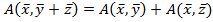 ; 2).
; 2). 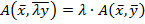 .
.
Билинейная форма 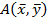 называется симметричной, если
называется симметричной, если 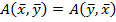 .
.
Билинейная форма 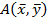 называется кососимметричной, если
называется кососимметричной, если 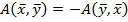 .
.
Матрицы билинейной формы, ее изменение при преобр.базисов
Пусть задан базис 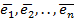 .Вектор
.Вектор 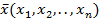 и вектор
и вектор 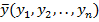 .Тогда билинейная форма
.Тогда билинейная форма 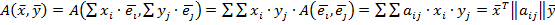 . Где
. Где 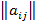 -матрица билинейной формы в заданном базисе.
-матрица билинейной формы в заданном базисе.
Матрица билинейной формы определяет некоторый линейный оператор.
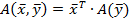 , где
, где 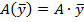
Тогда матрица линейного оператора преобразуется по следующему закону: 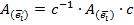 , где
, где 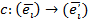 .
.
Рангом билинейной формы называется ранг матрицы этой формы.
Если определитель матрицы билинейной формы равен 0, то билинейная форма называется вырожденной. Если определитель не равен 0, то билинейная форма невырожденная.
Симметричные билинейные формы
Билинейная форма называется симметричной, если для любых векторов 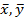 линейного пространства выполняется соотношение:
линейного пространства выполняется соотношение: 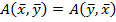
Квадратичные формы
Квадратичной формой называется симметричная билинейная форма от одинаковых аргументов. 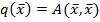 .
.
Свойства: 1). 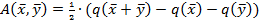 ; 2).Матрицей квадратичной формы называется матрица полярной билинейной формы.
; 2).Матрицей квадратичной формы называется матрица полярной билинейной формы.
Определение ранга вырожденности/невырожденности аналогичен определению для билинейной формы.
Канонический вид квадратичной формы
Каноническим видом квадратичной формы называется 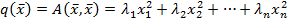 .
.
Определение: число ненулевых коэффициентов в каноническом виде квадратичной формы называется индексом инерции 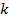 . Количество положительных коэффициентов называется положительным индексом инерции
. Количество положительных коэффициентов называется положительным индексом инерции 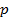 . Количество отрицательных – отрицательным индексом инерции
. Количество отрицательных – отрицательным индексом инерции 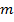 .
.
Метод Лагранжа канонизации квадратичной формы
Метод выделения полных квадратов.
Группируем слагаемые 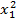 и все слагаемые, содержащие
и все слагаемые, содержащие 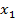 и выделяем полный квадрат относительно
и выделяем полный квадрат относительно 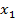 . Аналогичным способом поступаем со всеми остальными переменными в квадратичной форме. В результате получим квадратичную форму в каноническом виде.
. Аналогичным способом поступаем со всеми остальными переменными в квадратичной форме. В результате получим квадратичную форму в каноническом виде.
Замечание: Если в квадратичной форме отсутствуют квадраты переменных, то сначала производим преобразование: 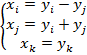
Классификация квадратичных форм.
1. 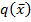 - знакоположительная, если
- знакоположительная, если 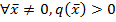 .
.
2. 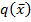 - знакоотрицательная, если
- знакоотрицательная, если 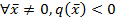 .
.
3. 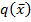 - знакопеременная, если
- знакопеременная, если 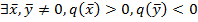 .
.
4. 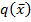 - квазизнакоположительная, если
- квазизнакоположительная, если 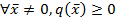 .
.
5. 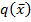 - квазизнакоотрицательная, если
- квазизнакоотрицательная, если 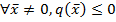 .
.
6. 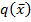 - квазизнакопеременная, если
- квазизнакопеременная, если 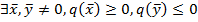
Классификация квадратичных форм с использованием индексов инерции.
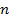 - размерность пространства
- размерность пространства
1. 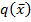 - знакоположительная, если
- знакоположительная, если 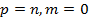 .
.
2. 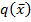 - знакоотрицательная, если
- знакоотрицательная, если 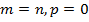 .
.
3. 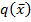 - знакопеременная, если
- знакопеременная, если 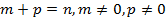 .
.
4. 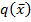 - квазизнакоположительная, если
- квазизнакоположительная, если 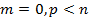 .
.
5. 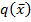 - квазизнакоотрицательная, если
- квазизнакоотрицательная, если 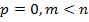 .
.
6. 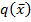 - квазизнакопеременная, если
- квазизнакопеременная, если 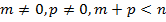 .
.
Критерий Сильвестра.
Пусть задана 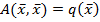 ,
, 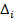 - угловые миноры матрицы квадратичной формы, тогда квадратичная форма знакоположительна, если
- угловые миноры матрицы квадратичной формы, тогда квадратичная форма знакоположительна, если 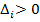 , и знакоотрицательна, если
, и знакоотрицательна, если 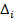 - знакочередующиеся, причем
- знакочередующиеся, причем 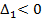 .
.
Теорема об инерции.
Теорема(закон инерции квадратичных форм): Количество положительных и отрицательных коэффициентов в канонической форме записи квадратичной формы не зависит от способа приведения квадратичной формы к каноническому виду.
