Стандарная схема исследования.

Первая производная:

1. Обл. определения, обл. знаяения.

2. Чётность, нечётность.

3. Периодичность.

4. Крит. т.

5. Экстремум.

Вторая производная:

1. Выпуклость, вогнутость.

2. Перегибы.

3. Асимптоты.

Первообразная и неопределенный интеграл.

Основные методы интегрирования. Интегрирование рациональных, иррациональных и тригонометрических функций.

Первообразная и неопределенный интеграл.

Опр1 (Первообразная).

Ф. 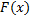в данном промежутке называется первообразной функцией для ф. или интегралом от , если во всём этом промежутке, является производной для ф. 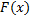или, что то же, служит для 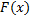дифференциалом: или .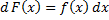

Теорема1.Если в некотором (конечном или бесконечном, замкнутом или нет) промежутке Ω ф. 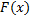есть первообразная для ф. , то и ф. , где 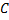– любая постоянная, также будет первообразной. Верно и обратное, каждая ф., первообразная для в промежутке Ω, может быть представлена в этой форме.

Док-во: То обстоятельство, что, наряду с 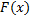, и является первообразной для , вполне очевидно, ибо . Пусть теперь 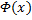будет любая первообразная для , такая что в промежутке Ω: 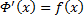. Т.к. ф. 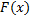и 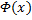в рассматриваемом пром. имеют одну и ту же производную, то они разнятся на постоянную: 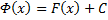, что и требовалось доказать.

Опр2 (Неопределенный интеграл).

В силу Т1 выражение , где 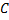– произвольная постоянная, представляет собой общий вид ф., которая имеет производную или дифференциал . Это выражение называется неопределённым интегралом . Обозначается символом: в котором (неявным образом) уже заключена произвольная постоянная. Произведение называется подинтегральным выражением, а ф. – подинтегральной функцией.

Свойства неопределённого интеграла.

1) .

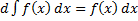2) .

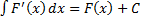Основные методы интегрирования.

Простейшие правила интегрирования.

1) 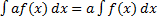, где , .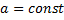

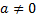2) .

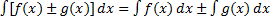3) Если 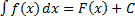, то .

Таблица основных интегралов.

1) .

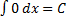2) .

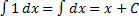3) 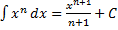, где .

4)

5) .

6) .

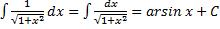7) .

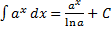8) .

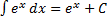9) .

10) .

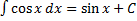11) .

12) .

13) .

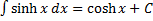14) .

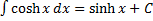15) .

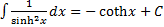16)

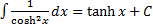
Замена переменной.

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если ф. непрерывна на , и ф. 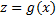имеет на непрерывную производную и 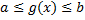, то

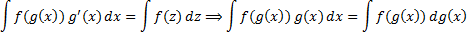
причём после интегрирования а правой части следует сделать обратную подстановку 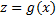.Пример: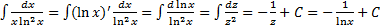

Метод интегрирования по частям.

Пусть ф. и 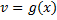имеют непрерывные производные. Тогда, по правилу дифференцирования произведения: 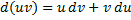, для выражения 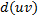первообразной будет 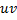, и имеет место формула: . Эта формула отражает суть правила интегрирования по частям.

Пример: Найти 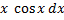. Положим , , 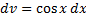следовательно , .

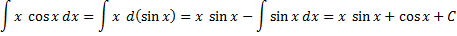
Интегрирование рациональных функций.

Интегрирование рац. ф. 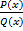, где и 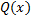– полиномы, выполняется в несколько шагов:

1) Преобразование неправильной рац. дроби.

Если дробь неправильная (т.е. степень больше 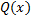), то разделим многочлен на :

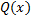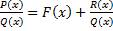, где 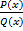– правильная рац. дробь.

Разложение знаменателя на простейшие дроби.

Запишем многочлен знаменателя 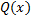в виде: 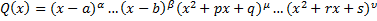, где квадратичные ф. являются несократимыми. т.е. не имеют действительных корней.