Опр3 (Предел интегральной суммы).

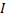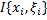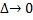Число называется пределом интегральной суммы при , если для любого положительного числа 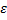можно указать такое положительное число 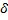, что для любого разбиения 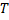сегмента , максимальная длина 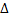частичных сегментов которого меньше 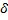, независимо от выбора точек 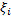на сегментах 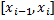выполняется неравенство: .

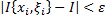Обозначается так: .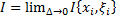

Опр4 (Интеграл Римана. Определённый интеграл).

Ф. называется интегрируемой (по Риману) на сегменте , если 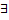конечный предел 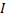интегральных сумм этой ф. при 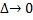. Указанный предел 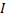называются определённым интегралом от ф. по сегменту и обозначается следующим образом: .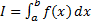

Формула Ньютона – Лейбница.

Основная формула интегрального исчисления.

Теорема1.Любая непрерывна на интервале 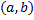ф. имеет на этом интервале первообразную. Одной из первообразных является ф.: 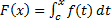, где 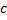– любая фиксированная т. интервала .

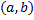Зам.: Первообразная также 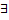у непрерывной на сегменте ф. И в качестве 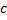можно взять .

Очевидно, что две любые первообразные данной ф. отличается на постоянную. Поэтому, по Т1 и замечанию к ней, можно утверждать что любая первообразная 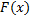непрерывной на сегменте функции имеет вид: 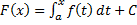, где 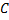– некоторая постоянная. Полагая в последней ф. 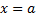, затем 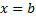, получим: 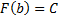, 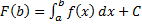. Из этих равенств получаем формулу Ньютона – Лейбница: .

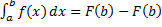Замена переменной и интегрирование по частям.

Замена переменной под знаком определённого интеграла.

Пусть выполнены следующие условия:

1) ф. непрерывна на сегменте ;

2) сегмент является множеством значений некоторой ф. 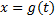, определённой на сегменте 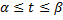и имеющие на этом сегменте непрерывную производную;

3) , .

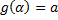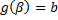Тогда справедлива формула: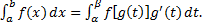

Называемая формулой замены переменной под знаком определённого интеграла.

Интегрирование по частям.

Пусть ф. 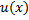и 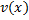имеют непрерывные производные на сегменте . Тогда имеет место следующая формула интегрирования по частям для определённых интегралов:

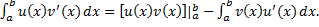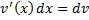Т.к. и 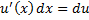, то формулу можно переписать: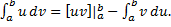

Несобственные интегралы.

Определённый интеграл 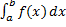называется несобственным интегралом, если выполняется хотя бы одно из условий:

1) Предел и 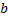(или оба предела) являются бесконечными;

2) Ф. имеет одну или несколько точек разрыва внутри интервала .

Бесконечные пределы интегрирования:

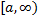1) Если непрерывна в интервале , то .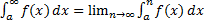

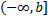2) Если непрерывна в интервале , то .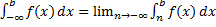

Если пределы 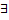и конечны, то несобственный интеграл сходится. Иначе расходится.

3) Если непрерывна на 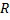, то .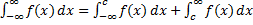

Если для 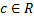оба интеграла в правой части сходятся, то и интеграл 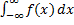тоже сходится. Иначе он расходится.

Геометрические приложения определенного интеграла.

Площадь плоской фигуры.

1) 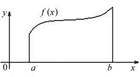Если ф. 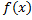непрерывна и неотрицательна на отрезке . Тогда площадь фигуры, ограниченной 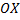, отрезками прямых 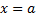, 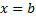и графиком ф. 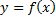, вычисляется по формуле: .

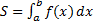2) 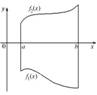Если 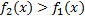на отрезке а так же непрерывны на нём, то площадь фигуры ограниченной прямыми 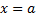, , 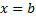графиками ф. 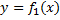, 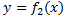вычисляется по формуле: .

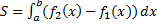3) 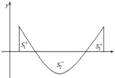Если ф. на отрезке принимает значения разных знаков, то площадь фигуры, заключённая между криво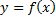й и 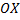, равна: .

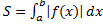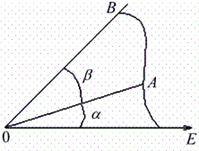Вычисление площади криволинейного сектора.

Пусть кривая 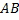задана в полярных координатах ур. 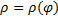, , 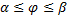причём 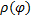– непрерывная и неотрицательная на отр. 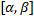ф. Фигуру, ограниченную кривой 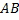и двумя полярными радиусами, составляющими с полярной осью углы 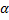и 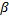, будем называть криволинейным сектором. Площадь вычисляется по формуле: .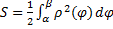