Свойства функций, непрерывных в точке.
Т1. (Арифм. опер.)
Пусть ф.  и
и 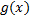 непрерывны в т.
непрерывны в т.  . Тогда ф.:
. Тогда ф.: 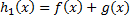 ,
, 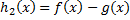 ,
, 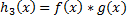 ,
, 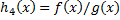 где
где 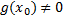 также непрерывны в точке
также непрерывны в точке  .
.
Т2. (Арифм. опер. при непр. справа( слева))
Аналогично Т1.
Свойства функций, непрерывных на отрезке.
Свойство1. (Первая теорема Вейерштрасса)
Если ф.  непр. на отрезке
непр. на отрезке  , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Зам.: Для интервала 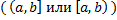 это утверждение несправедливо.
это утверждение несправедливо.
Док-во: Докажем, что ф.  ограничена сверху на сегменте
ограничена сверху на сегменте  (огр. снизу док. аналогично). Предположим противное, т.е. допустим,
(огр. снизу док. аналогично). Предположим противное, т.е. допустим,  не является огр. сверху на сегменте
не является огр. сверху на сегменте  . Тогда для
. Тогда для 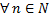 ,
, 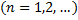 найдётся хотя бы одна т.
найдётся хотя бы одна т. 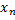 из сегмента
из сегмента  такая, что
такая, что 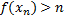 (иначе
(иначе  была бы огр. сверху на сегменте). Таким образом,
была бы огр. сверху на сегменте). Таким образом, 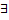 послед. знач.
послед. знач. 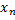 из сегмента
из сегмента  такая, что соответствующая послед. знач. ф.
такая, что соответствующая послед. знач. ф. 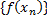 является б.б. В силу теоремы Больцано-Вейерштрасса (см. вопр.1) из послед.
является б.б. В силу теоремы Больцано-Вейерштрасса (см. вопр.1) из послед. 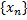 можно выделить подпослед., сходящуюся к т. ξ, принадлежащей, в силу 2 замечания к т. Б-В, сегменту
можно выделить подпослед., сходящуюся к т. ξ, принадлежащей, в силу 2 замечания к т. Б-В, сегменту  . Обозначим эту подпослед. символом
. Обозначим эту подпослед. символом 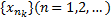 . В силу непрерывности ф.
. В силу непрерывности ф.  в т. ξ соотв. подпослед. значений ф.
в т. ξ соотв. подпослед. значений ф. 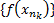 обязана сходится к
обязана сходится к 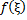 . Но это невозможно, ибо подпослед.
. Но это невозможно, ибо подпослед. 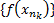 , будучи выделена из б.б. послед.
, будучи выделена из б.б. послед. 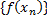 , сама является б.б. Получили противоречие. Ч.т.д.
, сама является б.б. Получили противоречие. Ч.т.д.
Свойство2 . (Вторая теорема Вейерштрасса).
Если ф.  непр. на отрезке
непр. на отрезке  , то она достигает на этом отрезке своих точных верхней и нижней граней (т.е. наибольшего и наименьшего знач.). Иными словами, на отрезке
, то она достигает на этом отрезке своих точных верхней и нижней граней (т.е. наибольшего и наименьшего знач.). Иными словами, на отрезке  найдутся такие т.
найдутся такие т. 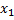 и
и 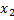 , что
, что 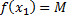 и
и 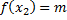 .
.
Свойство3 . (Первая теорема Больцано – Коши).
Если ф.  непр. на отрезке
непр. на отрезке  и имеет на концах отрезка значения противоположных знаков, то
и имеет на концах отрезка значения противоположных знаков, то 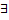 такая т. внутри отрезка, где
такая т. внутри отрезка, где 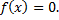
Свойство4 . (Вторая теорема Больцано – Коши).
Ф., непр. на отрезке  , принимает на этом отрезке все знач. между двумя произвольными величинами.
, принимает на этом отрезке все знач. между двумя произвольными величинами.
Свойство5 .
Если ф.  непрерывна в т.
непрерывна в т. 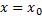 , то
, то 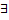 некоторая окрестность т.
некоторая окрестность т. 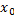 , в которой ф. сохраняет знак.
, в которой ф. сохраняет знак.
Равномерная непрерывность.
Опр7 (Равном. непр.)
Ф.  наз. равномерно непрерывной на отрезке
наз. равномерно непрерывной на отрезке  , если для
, если для 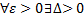 такое, что для
такое, что для 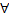 т.
т. 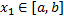 и
и 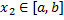 , таких что
, таких что 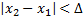 верно нерав.:
верно нерав.: 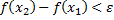 .
.
Зам.:Отличие равномерной от «обычной» непр. в том, что для 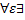 своё
своё 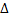 , не зависящее от
, не зависящее от 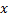 , а при «обычной» непр.
, а при «обычной» непр. 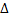 зависит от
зависит от 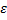 и
и 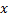 .
.
Свойство6 . (Теорема Кантора).
Ф., непрерывная на отрезке, равномерно непрерывна на нём.
Зам.: Только для отрезков.
Свойство6 .
Если ф.  определена, монотонна и непр. на. некотором промежутке, то и обратная ей ф.
определена, монотонна и непр. на. некотором промежутке, то и обратная ей ф. 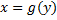 тоже однозначно определена, монотонна и непр.
тоже однозначно определена, монотонна и непр.
Классификация точек разрыва.
Опр8 (Общее опр. т. разрыва)
Рассмотрим некоторую ф.  , непр. в окрестности т.
, непр. в окрестности т. 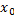 , за исключением быть может самой т. И так
, за исключением быть может самой т. И так 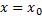 является точкой разрыва, если ф. не определена в этой т., или не является в ней непрерывной.
является точкой разрыва, если ф. не определена в этой т., или не является в ней непрерывной.
Типы точек разрыва:
Устранимый разрыв.
Т.  наз. точкой устранимого разрыва ф.
наз. точкой устранимого разрыва ф. 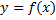 , если пред. знач. ф. в этой т.
, если пред. знач. ф. в этой т. 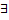 , но в т.
, но в т.  функция
функция  или не определена, или её частное значение
или не определена, или её частное значение 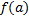 в т.
в т.  не равно пред. знач.
не равно пред. знач.
Разрыв 1-го рода.
Т.  наз. точкой разрыва 1-го рода, если в этой т. ф.
наз. точкой разрыва 1-го рода, если в этой т. ф.  имеет конечные, но не равные друг другу правое и левое предельные значения. т.е.
имеет конечные, но не равные друг другу правое и левое предельные значения. т.е. 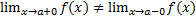 .
.
Разрыв 2-го рода.
Т.  наз. точкой разрыва 2-го рода, если в этой т. ф.
наз. точкой разрыва 2-го рода, если в этой т. ф.  не имеет по крайней мере одного из односторонних пред. знач. или если хотя бы одно из односторонних пред. знач. бесконечно.
не имеет по крайней мере одного из односторонних пред. знач. или если хотя бы одно из односторонних пред. знач. бесконечно.
Кусочно непрерывная ф.
Ф. 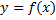 наз. кусочно непрерывной на отрезке
наз. кусочно непрерывной на отрезке  , если она непрерывна во всех внутренних т.
, если она непрерывна во всех внутренних т.  , за исключением, быть может, конечного числа т., в которых имеет разрыв 1-го рода и, кроме того, имеет односторонние предельные значения в т.
, за исключением, быть может, конечного числа т., в которых имеет разрыв 1-го рода и, кроме того, имеет односторонние предельные значения в т.  и
и 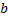 .
.
Ф. 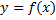 наз. кусочно непрерывной на интервале или бесконечной прямой, если она кусочно непрерывна на любом принадлежащем им отрезке.
наз. кусочно непрерывной на интервале или бесконечной прямой, если она кусочно непрерывна на любом принадлежащем им отрезке.
