Полуплоскости на которые прямая разбивает плоскость.

Пусть в плоскости дана прямая L. Будем говорить, что две точки принадлежат разным полуплоскостям, на которые L разбивает плоскость, если отрезок, соединяющий эти точки, пересекает L.

Две точки лежат в одной полуплоскости, если отрезок их соединяющий не пересекает L.

Пусть L:A*x+B*y+C=0, тогда при подстановке любой точки из одной полуплоскости в уравнение получим число больше нуля, такая полуплоскость называется положительной. А при подстановке любой точки из другой полуплоскость, будем называть отрицательной.

Доказательство:

1) Пусть точки Р₁ и Р₂ имеют разный знак при подстановке в уравнение (P₁(x₁,y₁), P₂(x₂,y₂)), докажем, что они лежат в разных полуплоскостях.

Проведем через точки Р₁ и Р₂ прямую L₁ . Запишем её параметрическое уравнение.

L₁:

Пусть t=0, тогда получим точку Р₁.

Пусть t=1, тогда получим точку Р₂.

Отрезку Р₁Р₂ соответствует tÎ[0,1]

Рассмотрим j(t)=A*( ))+B* ( )+C

Функция j(t) – непрерывна в частности на отрезке Р₁Р₂ (так как линейная функция от первого аргумента).

j(t)=A*(x₀+a*t) + B*(y₀+b*t) + C

j(0)=A*x₁+B*y₁+C>0

j(1)=A*x₂+B*y₂+C<0

j(t) – непрерывна и на концах отрезка принимает разные значения.

По теореме Больцмана (из матанализа): существует такое t₁ принадлежащее(0,1), что j(t₁)=0.

P’( ; )), P’Î[ Р₁Р₂]

P’ÎL=> P’=L∩ L₁.

Таким образом Р₁Р₂ пересекает L => Р₁ и Р₂ лежат в разных полуплоскостях.

2) Пусть Р₁ и Р₂ имеют одинаковый знак, Докажем, что они лежат в одной полуплоскости.

Проведем через точки Р₁ и Р₂ прямую L₁ . Запишем её параметрическое уравнение.

L₁:

Пусть t=0, тогда получим точку Р₁.

Пусть t=1, тогда получим точку Р₂.

Отрезку Р₁Р₂ соответствует tÎ[0,1]

Рассмотрим j(t)=A*( ))+B* ( )+C

j(0)=A*x₁+B*y₁+C>0- Р₁

j(1)=A*x₂+B*y₂+C<0- Р₂

Отрезку Р₁Р₂ соответствует tÎ[0,1]

j(t)=A*( ))+B* ( )+C=A*x₁ + A*t*x₂ – A*t*x₁ + B*y₁ + B*t*y₂ – B*t*y₁ + C=

= A*x₁*(1-t) + B*y₁(1-t) + A*t*x₂ + B*t*y₂ + C, C=C*(1-t)+C*t

=>(1-t)*( A*x₁+B*y₁+C) + t*( A*x₂+B*y₂+C), 1-t≥0, t≥0, при чем одновременно t≠0 и t-1≠0

=> на отрезке tÎ[0,1] j(t)>0;

Так как ни в какой точке отрезка j(t) неравно нулю, то отрезок Р₁Р₂ не пересекает прямую L => все точки отрезка Р₁Р₂ лежат в одной полуплоскости.

Взаимное расположение двух прямых в пространстве.

L₁: A₁*x+B₁*y+C₁=0

L₂: A₂*x+B₂*y+C₂=0

1) Прямые пересекаются

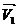=( -B₁; A₁), 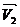=( -B₂; A₂)

L₁∩L₂<=>вектора 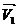и 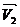не коллениарны, то есть 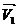≠k* , =>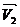

2) Прямые параллельны

3) Прямые совпадают

Уравнения плоскости.

1) Общее уравнение плоскости

Уравнение вида A*x+B*y+C*z+D=0 называется общим уравнением плоскости.

Уравнение A*x+B*y+C*z+D=0 является уравнением плоскости.

Уравнение является A*x+B*y+C*z+D=0 уравнением плоскости.

Доказательство:

Пусть есть плоскость γ. Точка Р₀(x₀,y₀,z₀) и вектора (x_a,y_a,z_a), (x_b,y_b,z_b) лежат в плоскости γ, Вектора и не коллениарны.

Пусть точка Р(x,y,z) не лежит в плоскости γ.

=( x-x₀,y-y₀,z-z₀)

Точка Р принадлежит плоскости γ тогда и только тогда, когда тройка векторов , , является компланарной, то есть < >=0.

=0

(x-x₀)* - (y-y₀)* + (z-z₀)* =0

Заменим: = A, = -B, =C

Так как вектора не коллениарны, то хотя бы один из трёх определителей не равен нулю.

(x-x₀)*A - (y-y₀)* B+ (z-z₀)* C=0

A*x + B*y + C*z – (A*x₀ + B*y₀ + C*z₀)=0, – (A*x₀ + B*y₀ + C*z₀)=D

A*x + B*y + C*z + D=0

Уравнение A*x + B*y + C*z +D=0 задаёт плоскость(Противоположно предыдущей теореме).

Доказательство:

A*x + B*y + C*z +D=0, A≠0 (1)

Р(x₀,y₀,z₀), пусть Р является решением уравнения (1)

A*x₀ + B*y₀ + C*z₀ + D=0 (2)

(1)-(2): A*(x-x₀) – B*(y-y₀)+ C*(z-z₀)=0 (3)

Уравнение (3) эквивалентно (1)

, А≠0

- это уравнение (3).

Из доказательства предыдущей теоремы следует, что уравнение (3) – уравнение плоскости, содержащей точку Р(x₀,y₀,z₀), (-B, A, 0), (-C, 0, A), вектора и не коллениарны => исходное уравнение задаёт плоскость.

Следствие: Пусть плоскость имеет уравнение A*x + B*y + C*z +D=0 => плоскость содержит 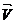(-B, A, 0) и (-С, 0, А).

Найдем вектор нормали к плоскости в прямоугольной системе координат.

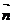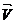=[ , ]=( , B*A, C*A)=(A, B, C)

Таким образом можно сформулировать геометрический смысл коэффициентов в общем уравнение плоскости: А,В,С – координаты вектора нормали.

2) Параметрическое уравнение плоскости

Уравнение вида называется параметрическим уравнением плоскости.

Уравнение вида является уравнением плоскости.

Доказательство:

Пусть есть плоскость γ. Точка Р₀(x₀,y₀,z₀) и вектора (x_a,y_a,z_a), (x_b,y_b,z_b) лежат в плоскости γ, Вектора и не коллениарны, также возьмем точку Р(x,y,z).

Точка Р принадлежит плоскости γ тогда и только тогда, когда тройка векторов , , является компланарной, то есть =u* +v*

(x-x₀,y-y₀,z-z₀)=u*(x_a,y_a,z_a) + v*(x_b,y_b,z_b)

(x-x₀,y-y₀,z-z₀)=(u*x_a, u*y_a, u*z_a) + (v*x_b, v*y_b, v*z_b)

Критерий компланарности вектора плоскости.

Вектор 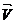(a, b, c) компланарен γ: A*x+B*y+C*z+D=0 тогда и только тогда, когда A*a+B*b+C*c=0.

Доказательство:

Возьмем точку Р₀(x₀,y₀,z₀) лежащую в плоскости γ, приложим к этой точке вектор 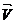, пусть конец этого вектора в точке Р₁=(x₁,y₁,z₁)=(x₀+a,y₀+b,z₀+c).

Вектор 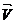компланарен γ тогда и только тогда, когда точка Р₁ принадлежит плоскости γ.

Значит: A*x₁+B*y₁+C*z₁+D=0

A*(x₀+a)+B*(y₀+b)+C*(z₀+c)+D=0

A*a + B*b + C*c + (A*x₀ + B*y₀ + C*z₀) + D=0, A*x₀ + B*y₀ + C*z₀= -D

=> A*a + B*b + C*c =0