Сведение задачи теории игр к задаче линейного программирования

Для определения 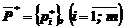и 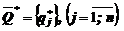используют метод сведения задачи теории игр к задаче линейного программирования.

Для игрока А задача формулируется в виде:

Найти минимум целевой функции 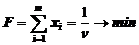, где переменные 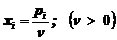удовлетворяют системе ограничений (матрица М транспонируется!)

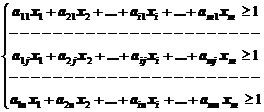
Для игрока В задача формулируется в виде:

Найти маскимум целевой функции 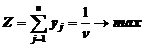, где переменные 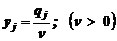, удовлетворяют системе ограничений

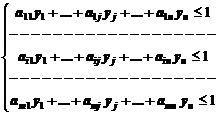
Доминирование матричной игры

Доминировать матричную игру, значит, сократить ее размер.

Для этого пользуются следующими положениями.

Если в матрице имеются одинаковые (дублирующие) строки, то одна из них оставляется, а другие убираются.

Если в матрице имеются одинаковые (дублирующие) столбцы, то один из них оставляется, а другие убираются.

Если все элементы i – й строки матрицы М меньше или равны соответствующих элементов k – й строки, то i –я стратегия игрока А называется доминирующей и ее следует убрать.

Если все элементы r – го столбца матрицы М больше или равны соответствующих элементов j – го столбца, то для игрока Вr – я стратегия является доминирующей и ее следует убрать.

Игры с природой

На практике часто встречается класс матричных игр, в которых стратегия второго игрока неопределена. Это, так называемые, «игры с природой». Например, нас интересует вопрос об объемах поставок продукции на рынок в условиях полной неопределенности о величине спроса на эту продукцию.

В этом случае выбор стратегии осуществляется на основе критериев, которые позволяют оценить «среднюю прибыль».

Критерий Вальда:

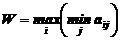
Критерий Сэвиджа:

,

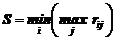где 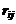- элементы матрицы R – матрицы риска. Эта матрица составляется по правилу: в столбце определяется наибольший элемент и из этого числа вычитаются последовательно все элементы этого столбца.

Критерий Гурвица:

,

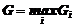где 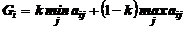, значение параметра k 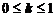- задается самим исследователем.

Пример 1. Для заданной матрицы игры

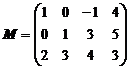
1) Показать существование или отсутствие оптимальных стратегий.

Решение.

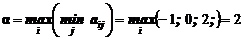
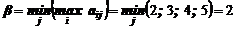
Выводы:

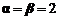, решение в чистых стратегиях;

Седловая точка ;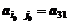

Игрок А выбирает чистую стратегию ;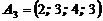

Игрок В выбирает стратегию 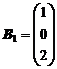. Цена игры .

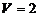2) Выполнить доминирование матрицы М.

.

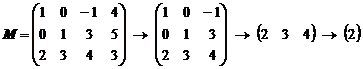Решение.

1. Элементы 4-го столбца превосходят соответствующие элементы 1-го столбца. Значит, этот столбец доминирующий. Его убираем из матрицы.

2. Во второй матрице доминирующими являются 1-я и 2-я строки, так как их элементы меньше соответствующих элементов 3-й строки. Их убираем.

3. В третьей матрице доминирующими являются 2-й и 3-й столбцы.

4. Получили матрицу, состоящую из одного элемента .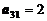

Пример 2. Свести исходную матричную игру к паре двойственных ЗЛП.

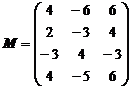
Решение.

1.

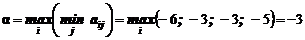
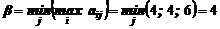
Выводы: 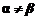. Задача решается в смешанных стратегиях.

2. Сведем матричную игру к паре двойственных ЗЛП.

Сначала получим матрицу с положительными элементами. Для этого к каждому элементу матрицы М прибавим число 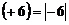, то есть абсолютную величину наименьшего элемента матрицы М.

Получим матрицу :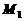

.

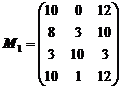ЗЛП для игрока А:

переменные ;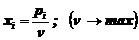

целевая функция ;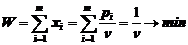

система ограничений: (матрицу М₁ транспонируем)

.

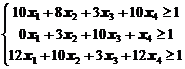ЗЛП для игрока В:

переменные ;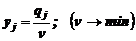

целевая функция ;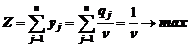

система ограничений:

.

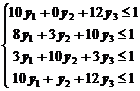Пример 3. Полагая матрицу

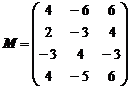
матрицей игры с природой найти решение игры, используя критерии Вальда, Сэвиджа и Гурвица при k = 0,7.

Решение.

1. Критерий Вальда:

.

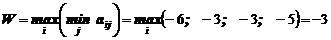Вывод: Активные стратегии А₂ или А₃.

2. Критерий Сэвиджа:

Построим сначала матрицу рисков R.

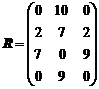
Затем вычислим

.

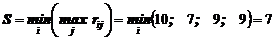Вывод: Активная стратегия А₂ .

3. Критерий Гурвица (k = 0,7)

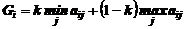
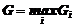
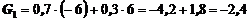
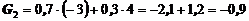
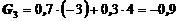
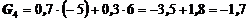
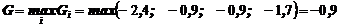
Вывод: Активные стратегии А₂ или А₃.

Ответ. Рекомендация – выбрать стратегию А₂.