Интегральная теорема Лапласа

В том случае, когда требуется найти вероятность того, что событие А появится не менее к₁ и не более к₂ раз в n опытах, используются интегральные формулы Лапласа:

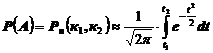(18)

или

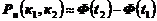, где

, , .

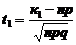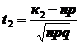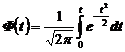Здесь функция 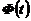–функция Лапласа находится по специальным таблицам 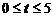при . При 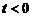следует иметь ввиду, что 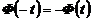. При 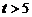полагают .

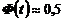Пример 18. При выпуске продукции 20% изделий не подвергаются контролю на качество. Какова вероятность того, что среди 400 изделий, выбранных случайно, окажется от 70 до 100 непроверенных изделий.

Решение. Из условия задачи вероятность того, что изделие не пройдет контроль равна 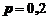. Тогда 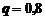. Найдем искомую вероятность по формуле

.

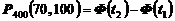Найдем

,

.

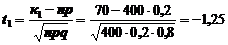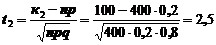Теперь по таблице находим

; .

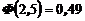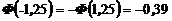Окончательно получим

.

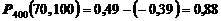Формула полной вероятности

Если событие В происходит вместе с одним из событий А₁, А₂,…, А_n, образующих полную группу несовместимых событий, то имеет место формула

.

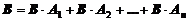Тогда вероятность события В находится по формуле полной вероятности

.

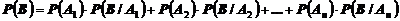Пример 19. В магазин поступили замки, изготовленные на трех заводах. Установлено, что продукция первого завода содержит 20% бракованных изделий, второго – 10%, третьего – 5%. Среди замков, взятых на реализацию, 30% изготовлено на первом заводе, 20% - на втором, 50% - на третьем. Какова вероятность купить исправный замок.

Решение. Обозначим события:

В – куплен исправный замок,

А₁ – куплен замок, изготовленный на первом заводе,

А₂ – куплен замок, изготовленный на втором заводе,

А₃ – куплен замок, изготовленный на третьем заводе.

Тогда, так как события А₁, А₂, А₃ несовместимые и образуют полную группу, и событие В происходит вместе с одним из этих событий, искомую вероятность найдем по формуле полной вероятности.

Представим событие В как

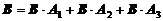
Эта формула означает, что куплен исправный замок с первого завода или со второго, или с третьего завода.

.

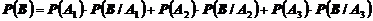Найдем все вероятности, входящие в эту формулу. Из условия задачи имеем

, , .

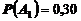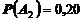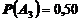Условные вероятности равны

.

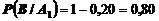
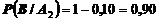
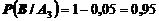Итак, получим

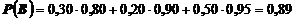
Формула Бейеса

Эта формула применяется для нахождения условной вероятности события А_i в предположении, что событие В уже произошло. При этом известно, что событие В может произойти вместе с одним из несовместимых событий А₁, А₂, … А_n, образующих полную группу.

Формула Бейеса имеет вид:

.

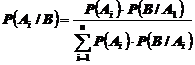Пример 20. Товар находится в трех одинаковых упаковках. В первой упаковке 20 изделий первого сорта. Во второй – 10 изделий первого сорта и 10 изделий второго сорта. В третьей – 20 изделий второго сорта. Из взятой наугад упаковки вынули изделие первого сорта. Найти вероятность того, что это изделие взято из первой упаковки.

Решение. Обозначим события:

В – взято изделие первого сорта,

А₁ - взято изделие из первой упаковки,

А₂ - взято изделие из второй упаковки,

А₃ - взято изделие из третьей упаковки.

События А₁, А₂, А₃ образуют полную группу. Нужно найти условную вероятность

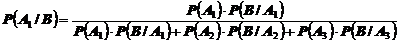
Теперь найдем вероятности всех этих событий. Так как события А₁, А₂, А₃ равновероятны, то

.

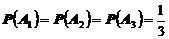Вероятность взять изделие первого сорта из первой упаковки равна

.

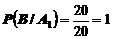Вероятность взять изделие первого сорта из второй упаковки равна

.

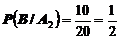Вероятность взять изделие первого сорта из третьей упаковки равна

.

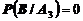Тогда, окончательно, получим

.

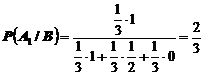Понятие случайной величины

Случайная величина (СВ) – второе основное понятие теории вероятностей. В отличие от случайного события, случайная величина это переменная.

Определение. Случайной величиной называется переменная, которая может принимать различные значения в зависимости от обстоятельств.

Примеры: урожай картофеля с га, число родившихся за день мальчиков, рост девочек определенного возраста и т.д.

Случайные величины принято обозначать последними заглавными буквами латинского алфавита: X, Y, Z и т.д. Значения этих величин обозначаются соответствующими малыми буквами: х, у, z и т.д.

Классификация СВ

Дискретными называются СВ, которые принимают отдельные возможные значения (ДСВ).

Например: число, присутствующих на семинаре студентов из группы 25 человек, может иметь значения 0, 1, 2, …, 25.

Непрерывными называются СВ, которые могут принимать все значения из некоторого конечного или бесконечного промежутка (НСВ).

Например: время работы электрической лампочки, рост мальчиков одного возраста.

Способы задания случайных величин

Дискретная СВ считается заданной, если известны все ее возможные значения х₁, х₂, …, х_n и вероятности, с которыми принимаются эти значения р₁, р₂, …, р_n. Эти данные принято записывать в форме таблицы:

Х	х1	х2	…	хn
Р	р1	р2	…	рn

Эту таблицу называют рядом распределения ДСВ.

Отметим, что события Х = х₁,Х = х₂,…,Х = х_n (т.е. СВ Х принимает значение х₁ и т.д.) образуют полную группу, так как они несовместимые и одно из них обязательно произойдет. Следовательно, сумма вероятностей p_iравна 1:

.

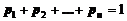Пример 21. Фирму обслуживает три автомашины. Вероятность поломки каждой в течение года равна 0,6. Составить ряд распределения СВ – числа поломавшихся автомашин в течение года.

Решение. Х – число, поломавшихся автомашин может быть равно 0, 1, 2, 3. Так как вероятность поломки постоянна, то воспользуемся формулой Бернулли (16).

Вероятность, что ни одна автомашина не сломается, т.е. Х примет значение равное нулю, находится как

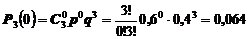
Вероятность, что сломается одна машина из трех равна

.

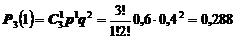Аналогично находятся вероятности поломки двух и трех автомашин

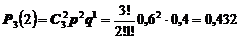
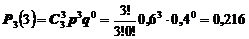
Теперь составим ряд распределения Х

Х
Р	0,064	0,288	0,432	0,216

Очевидно, что если ДСВ имеет много значений, то задавать ее в форме ряда распределения неудобно. Поэтому разработан другой способ – с помощью функции распределения.

Функцией распределения СВ Х называется функция 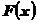, равная вероятности того, что СВ Х примет значение, меньше данного х.

С помощью функции распределения можно задать и непрерывную СВ.

Обычно для дискретной СВ функцию распределения представляют графически в виде кусочно–постоянной функции.

Пример 22. Составить функцию распределения по условиям примера 21.

Решение. Так как по условию Х не принимает значений, меньших нуля, то вероятность события 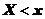при 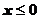равна нулю (невозможное событие).

При 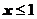вероятность события 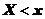равна 0,064, так как в этом случае СВ Х может иметь только значение 0 с вероятностью 0,064.

В промежутке 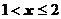, вероятность события 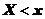будет равна сумме вероятностей 0,064 + 0,288 = 0,352, так как в этом случае СВ может принимать два значения 0 и 1. Тогда по теореме сложения вероятностей и получаем указанное значение.

Рассуждая аналогично, получим, что вероятность события 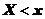в промежутке 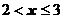равна сумме

0,064 + 0,288 + 0,432 = 0,784

Запишем теперь функцию распределения в виде

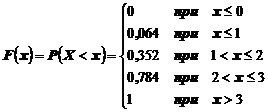
Построим график функции распределения

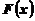
1,0

0,784

0,352

0,064

0 1 2 3 х

Как видно, функция 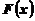постоянна на интервалах, где нет ее значений, и имеет скачки в точках, соответствующих ее значениям. Эти скачки равны вероятностям, с которыми СВ принимает свои значения.

Заметим, что функция 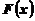отражает вероятности событий, и, следовательно, не может иметь значений меньше 0 и больше 1.