Интегральная теорема Муавра-Лапласа

Пусть 0< p <1, тогда для схемы Бернулли при n ® для любых a и b справедлива формула

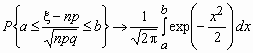
Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу

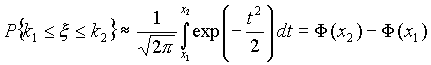
Где 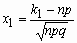, , 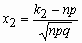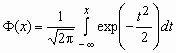функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

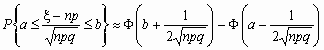и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу

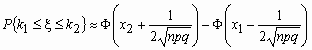где ,

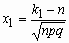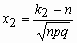
14) Теорема Ляпунова— теорема в теории вероятностей, устанавливающая некоторые общие достаточные условия для сходимости распределения сумм независимых случайных величин к нормальному закону.

Часто приходится иметь дело с такими случайными величинами, которые являются суммами большого числа независимых случайных величин. При некоторых весьма общих условиях оказывается, что эта сумма имеет распределение, близкое к нормальному, хотя каждое из слагаемых может не подчиняться нормальному закону распределения вероятностей. Эти условия были найдены Ляпуновым и составляют содержание теоремы, названной его именем.

Пусть с ξ1,ξ2,...,ξn,… последовательность попарно независимых случайных величин с математическими ожиданиями M(ξi) = αi и дисперсиями D

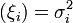причём эти величины обладают следующими двумя свойствами:

1) Cуществует такое число L, что для любого i имеет место неравенство 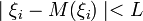т, е. все значения случайных величин, как говорят, равномерно ограничены, относительно математических ожиданий;

2) Сумма 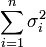неограниченно растёт при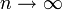

Тогда при достаточно большом n сумма ξ = ξ1 + ξ2 + ... + ξn имеет распределение, близкое к нормальному.

Пусть α и σ математическое ожидание и дисперсия случайной величины ξ = ξ1 + ξ2 + ... + ξn. .Тогда

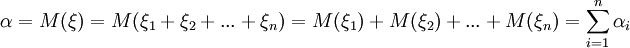
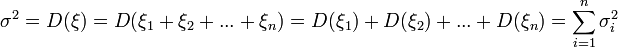
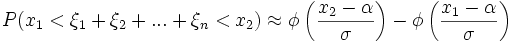Где φ — интеграл вероятности.Ξερω/

15) Первым этапом статистического изучения вариации являются построение вариационного ряда - упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.

Существуют три формы вариационного ряда: ранжированный ряд, дискретный ряд, интервальный ряд. Вариационный ряд часто называют рядом распределения. Этот термин используется при изучении вариации как количественных, так и неколичественных признаков. Ряд распределения представляет собой структурную группировку.

Если численность единиц совокупности достаточно велика, ранжированный ряд становится громоздким, а его построение, даже с помощью ЭВМ, занимает длительное время. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака.

Если признак принимает небольшое число значений, строится дискретный вариационный ряд. Примером такого ряда является распределение футбольных матчей по числу забитых мячей (табл. 5.1). Дискретный вариационный ряд - это таблица, состоящая из двух строк или граф: конкретных значений варьирующего признака хi и числа единиц совокупности с данным значением признака fi частот (f - начальная буква англ. слова frequency).

Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.

Интервальный вариационный ряд представляет собой таблицу, (состоящую из двух граф (или строк) — интервалов признака, вариация которого изучается, и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа от общей численности совокупности (частостей).

16) Корреляционная зависимостьмежду случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии.

Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости оценить ее силу по величине коэффициента регрессии. Например, ясно, что корреляционная зависимость возраста Y учеников средней школы от года Х их обучения в школе является, как правило, более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возраcте, чем у школьников одного и того же класса.

Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции, определяемого формулой:

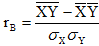
где σX и σY выборочные средние квадратические отклонения величин Х и Y, которые вычисляются по формулам:

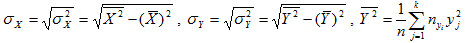
Следует отметить, что основной смысл выборочного коэффициента линейной корреляции rB состоит в том, что он представляет собой эмпирическую (т.е. найденную по результатам наблюдений над величинами Х и Y) оценку соответствующего генерального коэффициента линейной корреляции r: r=rB (9)

Принимая во внимание формулы:

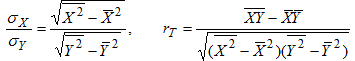
видим, что выборочное уравнение линейной регрессии Y на Х имеет вид:

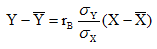
где . 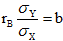То же можно сказать о выборочном уравнений линейной регрессии Х на Y

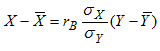
Основные свойства выборочного коэффициента линейной корреляции:

1. Коэффициент корреляции двух величин, не связанных линейной корреляционной зависимостью, равен нулю.

2. Коэффициент корреляции двух величин, связанных линейной корреляционной зависимостью, равен 1 в случае возрастающей зависимости и -1 в случае убывающей зависимости.

3. Абсолютная величина коэффициента корреляции двух величин, связанных линейной корреляционной зависимостью, удовлетворяет неравенству 0<|r|<1. При этом коэффициент корреляции положителен, если корреляционная зависимость возрастающая, и отрицателен, если корреляционная зависимость убывающая.

4. Чем ближе |r| к 1, тем теснее прямолинейная корреляция между величинами Y, X.

По своему характеру корреляционная связь может быть прямой и обратной, а по силе – сильной, средней, слабой. Кроме того, связь может отсутствовать или быть полной.

17) Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.

Пусть случайная величина x (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия Dx = s ² (s > 0). Из генеральной совокупности (на множестве объектов которой определена случайная величина) делается выборка объема n. Выборка x₁, x₂,..., x_n рассматривается как совокупность n независимых случайных величин, распределенных так же как x (подход, которому дано объяснение выше по тексту).

Ранее также обсуждались и доказаны следующие равенства:

Mx₁ = Mx₂ = ... = Mx_n = Mx;

Dx₁ = Dx₂ = ... = Dx_n = Dx;

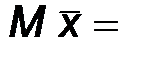Mx;

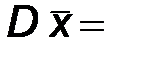Dx /n;

Достаточно просто доказать (мы доказательство опускаем), что случайная величина 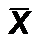в данном случае также распределена по нормальному закону.

Обозначим неизвестную величину Mx через a и подберем по заданной надежности g число d > 0 так, чтобы выполнялось условие:

P(| 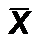– a| < d) = g

Так как случайная величина 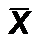распределена по нормальному закону с математическим ожиданием M 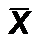= Mx = a и дисперсией D 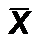= Dx /n = s ²/n, получаем:

P(| 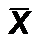– a| < d) =P(a – d < 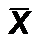< a + d) =

=

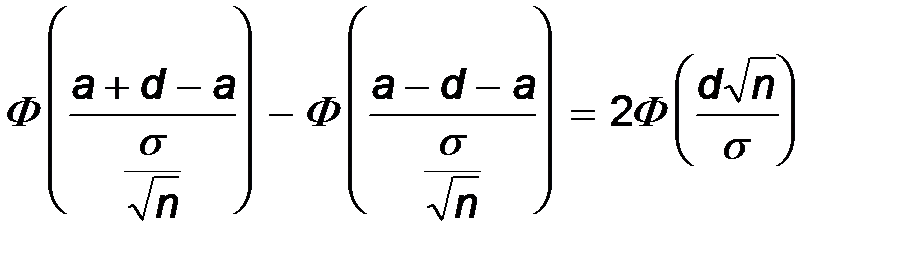
Осталось подобрать d таким, чтобы выполнялось равенство 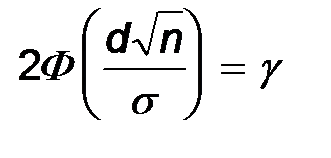или .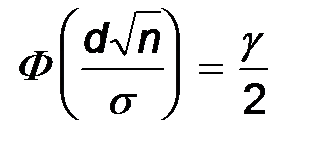

Для любого g Î[0;1] можно по таблице найти такое число t, что
F( t )= g / 2. Это число t иногда называют квантилем.

Теперь из равенства

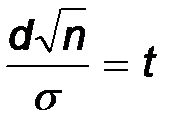
определим значение d: .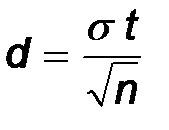

Окончательный результат получим, представив формулу (1) в виде:

.

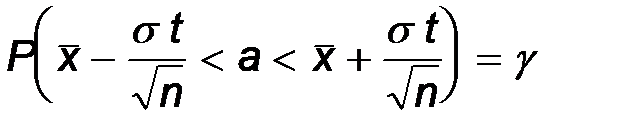Смысл последней формулы состоит в следующем: с надежностью g доверительный интервал

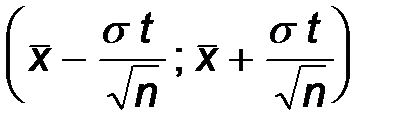
покрывает неизвестный параметр a = Mx генеральной совокупности. Можно сказать иначе: точечная оценка 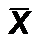определяет значение параметра Mx с точностью d=s t / 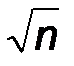и надежностью g.