Случайных величин с заданным законом распределения

Цель работы: приобретение навыков построения вероятностных моделей систем; моделирование случайных величин с заданным законом распределения; анализ статистических характеристик имитируемых случайных процессов (шумов).

Общие положения

В основу многих вероятностных моделей процессов и явлений могут быть положены законы распределения случайных величин. Например, известно, что относительная частота рождений младенцев мужского пола заметно не отличается от значения 0,515, если учтено достаточно большое число рождений. Эта частота не зависит от местности, где проводятся наблюдения, или от этнического состава населения. В свою очередь, если определять относительную частоту распада изотопа радия 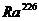за 100 лет, то всегда будет получаться величина 0,04184.

Для очень многих событий установлены те или иные законы распределений. Например, распределение Пуассона применяют при исследовании рисков отказов оборудования, возникновения пожаров, производственных аварий, природных катастроф типа тайфунов, смерчей; распределения Вейбулла, Парето – при исследовании землетрясений, наводнений, извержений вулканов, крупных техногенных катастроф, катастрофических пожаров; гамма-распределение – при изучении риска смертельного травматизма, числа промышленных аварий и т.д.

В физике имеется масса примеров, которые связаны с оценкой состояния физических систем на основе определения вероятности событий, свойственных данным системам. Известно, что значения скоростей молекул подчиняются распределению Максвелла, ошибки наблюдений – нормальному распределению, случайные блуждания частиц – распределению арксинуса, сила притяжения (отталкивания), действующая на частицу газа, который представляет собой совокупность заряженных ионов – распределению Хольцмарка и т.д.

В системах телекоммуникаций замирания в канале связи при отсутствии прямой видимости между абонентом и базовой станцией имеют рэлеевский закон распределения; аддитивные помехи (шумы) часто описываются нормальным (гауссовским) законом распределения; временные интервалы между вызовами в телефонных сетях связи обычно имеют экспоненциальный закон распределения.

На практике часто приходится выбирать вид модельного распределения не имея достаточного объема данных, чтобы можно было бы проверить его адекватность. Выбор вида распределения обычно основывается на прошлом опыте, на знании механизма конкретного явления или на теоретических предпосылках.

Краткие сведения о распределениях вероятностей случайных величин

Известно, что основной вероятностной характеристикой случайных величин является плотность распределения вероятности. Для различных вероятностных распределений зависимости для определения плотности вероятности имеют вид:

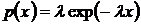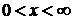, – для показательного закона распределения;

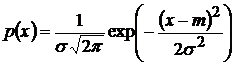– для нормального (гауссова) закона распределения;

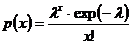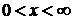, – для пуассоновского закона распределения;

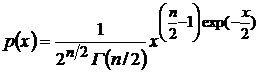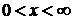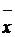
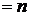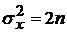, , , – для закона распределения хи-квадрат (частный случай при 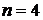– рэлеевское распределение - ;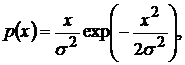

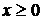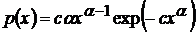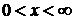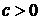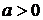, , , – для закона распределения Вейбулла;

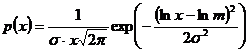– для логнормального закона распределения;

Источники случайных чисел

Физические источники настоящих случайных чисел не отличаются многообразием. Шумы, такие как детекторы событий ионизирующей радиации, дробовой шум в резисторе или космическое излучение могут быть источниками случайных чисел. Однако устройства, использующие эти явления, применяются редко. Более простым решением является создание некоторого набора из большого количества случайных чисел и опубликование его в некотором словаре в таблицах. Однако такие наборы обеспечивают ограничительные последовательности случайных чисел по сравнению с тем количеством, которое требуется на практических приложений.

Чаще всего используют для генерации случайных чисел различные алгоритмы. Эти алгоритмы заранее определены и, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. В то же время, если выбрать хороший алгоритм, полученная численная последовательность будет удовлетворять большинству тестов на случайность. Числа, генерируемые алгоритмами и удовлетворяющие статистическим критериям, называют псевдослучайными числами.

В основе моделирования случайных величин лежат методы имитационных случайных чисел с помощью генераторов.

Очевидно, что абсолютно случайные числа нельзя получить, используя определённый алгоритм. Однако можно создать такую последовательность чисел, которая будет обладать многими свойствами случайных чисел. Такие числа называются псевдослучайными. Впервые способы создания псевдослучайных чисел предложил Джон фон Нейман в 1946 г.

Генератор псевдослучайных чисел (ГПСЧ) представляет собой алгоритм, генерирующий некоторую последовательность чисел, которые почти независимы друг от друга и подчиняются заданному вероятностному распределению (обычно равномерному).

Современная информатика широко использует псевдослучайные числа в самых разных приложениях: в методе Монте-Карло, при имитационном моделировании, в криптографии и т.д. При этом от качества применяемых ГПСЧ напрямую зависит качество получаемых результатов.

Детерминированные ГПСЧ

Детерминированный алгоритм не может генерировать абсолютно случайные числа, он может только генерировать последовательность с некоторыми случайными свойствами.

Для создания таких алгоритмов используют различные методы, например, линейный конгруэнтный метод, метод Фибоначчи с запаздываниями, регистр сдвига с линейной обратной связью, регистр сдвига с обобщенной обратной связью.

Из современных ГПСЧ широкое распространение также получил алгоритм «вихрь Мерсенна», предложенный в 1997 году Мацумото и Нисимурой и основанных на свойствах простых чисел Мерсенна. Его достоинствами являются колоссальный период (2¹⁹⁹³⁷ − 1), равномерное распределение в 623 измерениях, быстрая генерация случайных чисел (в 2-3 раза быстрее, чем другие ГПСЧ). Однако, существуют алгоритмы, распознающие последовательность, порождаемую вихрем Мерсенна, как неслучайную.