Решение матричной игры в смешанных стратегиях

В предыдущем разделе мы выяснили, что матричная игра с нулевой суммой имеет решение в чистых стратегиях тогда и только тогда, когда нижняя и верхняя её цены совпадают. А что же делать в противном случае? Тогда теория игр рекомендует игрокам чередовать имеющиеся у них стратегии таким образом, чтобы каждая из них применялась с постоянной частотой. Таким образом, мы переходим от рассмотрения одной игры к изучению достаточно длинной серии повторений нашей игры, и будем интересоваться средними выигрышами игроков.

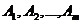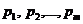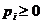Определение. Применение игроком A в серии повторений игры своих стратегий с частотами (где и 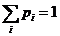) называется смешанной стратегией 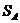игрока A и обозначается

.

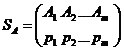Замечание. Мы говорим, что стратегия 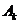применяется с частотой 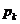, если в ходе 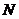повторений игры ( 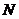достаточно велико) игрок A применял её примерно 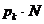раз (при этом отношение количества применений стратегии 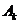к числу 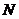стремится к 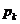при ).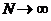

Аналогично определяется и смешанная стратегия для игрока B. Заметим, что чистая стратегия является частным случаем смешанной: а именно, когда все частоты нулевые, кроме одной равной единице. Понятия оптимальной смешанной стратегии и решения игры в смешанных стратегиях определяются аналогично предыдущему разделу. В частности, решить игру в смешанных стратегиях означает найти устойчивую пару смешанных стратегий, т.е. такую, когда ни одному из игроков не выгодно отклоняться от своей смешанной стратегии при условии, что второй игрок придерживается своей. При этом средний выигрыш игрока A, соответствующий применению таких стратегий,будет называться ценой игры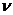 .Оказывается, что цена игры заключена между нижней и верхней ценами игры:

.

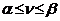Решение в чистых стратегиях может и не существовать, однако следующая теорема фон Нейманаутверждает, что решение в смешанных стратегияхвсегда существует:

Теорема. Каждая конечная игра имеет по крайней мере одно решение среди смешанных стратегий.

Для нахождения решения в виде смешанных стратегий бывает полезным следующее утверждение:

Теорема (об активных стратегиях).Если один из игроков придерживается своей оптимальной смешанной стратегии, то средний выигрыш остаётся неизменным и равным цене игры при условии, что второй игрок применяет любую из своих активных стратегий, входящих в его оптимальную стратегию.

При этом активнойназывается стратегия, применяемая с ненулевой частотой.

К примеру, в смешанной стратегии 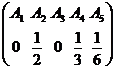активными являются стратегии .

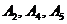Мы уже использовали игру в хоккей для разъяснения предыдущего материала, а теперь отправимся на футбольный матч! Одна из самых зрелищных, волнующих и даже драматических его частей – это случающаяся иногда серия послематчевых пенальти. Рассмотрим «дуэль» голкипера и футболиста с точки зрения теории игр. Все знают, что успех или неуспех голкипера в удержании ворот зависит главным образом от того, угадает ли он, в какой угол будет бить нападающий. Рассмотрим форварда A и голкипера B, уже неоднократно встречавшихся между собой в подобных поединках. Будем считать для простоты, что у A имеется всего две стратегии: 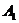− ударить в правый от вратаря угол ворот и 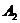− ударить в левый угол. Соответственно, пусть у B имеется выбор: 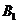− «прыгнуть» вправо от себя и 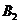− «прыгнуть» влево. В силу предположения примера, в каждом из четырех получающихся случаев считается известной статистика взятия ворот (в скольких процентах случаев был забит гол); например, такая:

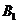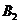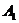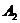(12.1)

Очевидно, что данные проценты могут считаться выигрышем форварда A (в профессиональном футболе – в буквальном денежном смысле, если форвардам платят определённую сумму за каждый забитый мяч) и проигрышем голкипера B. (Не думаю, что вратарей штрафуют за пропущенные мячи; но если мы хотим рассматривать нашу игру как игру с нулевой суммой, то выигрыши вратаря должны выражаться соответственно числами −20, −95, −90 и −25. Ясно, что для вратаря ничего не изменится в относительном предпочтении стратегий, если ко всем его выигрышам прибавить одно и то же число. Так вот, если прибавить число 100, мы получим новые выигрыши вратаря 80, 5, 10 и 75, имеющие прозрачный смысл как вероятности в процентах удержания ворот вратарём – и за это в профессиональном клубе ему могут платить соответствующие деньги. Единственная гипотеза тогда должна заключаться в том, что гонорар форварду за забитый мяч равен гонорару вратаря за отражённый.)

Итак, имеем конечную игру двух игроков с нулевой суммой. Легко подсчитываем, что 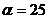и 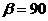. Видим, что решений игры в чистых стратегиях не существует. (И неудивительно: никто из форвардов не будет бить раз за разом в один и тот же угол! Аналогично, и вратарь не будет всё время «прыгать» в одну и ту же сторону!) Будем искать оптимальные смешанные стратегии, существующие по теореме Неймана. Пусть искомая стратегия для A имеет вид:

.

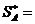
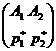В силу очевидного замечания выше, каждая из стратегий вратаря является активной. По теореме об активных стратегиях средний выигрыш форварда при условии, что он применяет 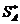, а вратарь – всё время 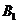или всё время 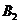, равен цене игры 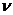.Подсчитаемсредний выигрыш за 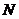повторений игры в первом из этих случаев. Нападающий в примерно в 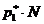случаев применял 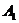и получал выигрыш 20 (т.к. вратарь всё время придерживался 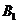); а примерно в 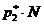случаев применял 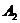и получал по той же причине выигрыш 90. В целом за серию общий выигрыш форварда равнялся 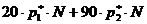, а, значит, средний его выигрыш равнялся 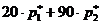. Аналогично рассуждая во втором случае, получаем следующую систему уравнений для определения 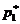и :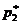

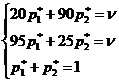
Приравнивая левые части первых двух уравнений и решая полученную систему, находим 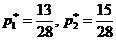. Итак, оптимальная смешанная стратегия нападающего получена. Цена игры при этом будет равняться 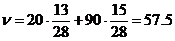. Таким образом, следуя данной смешанной стратегии (т.е. с вероятностью 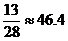% пробивая в правый от вратаря угол ворот, и с вероятностью 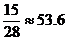% − в левый), нападающий будет забивать в среднем 57.5% мячей.

Рассмотри теперь оптимальную смешанную стратегию для нашего голкипера. Пусть она записывается в виде 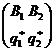. Тогда, применяя теорему об активных стратегиях и рассуждая как выше, получим следующую систему

,

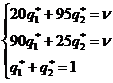из которой находим 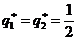. Таким образом, оптимальная смешанная стратегия вратаря будет заключаться в том, чтобы «прыгать» вправо и влево с равной частотой. При этом, увы, он будет пропускать более половины – 57.5 процентов – мячей. Тем не менее, это лучшее, на что он может рассчитывать в данной ситуации; поскольку по определению пары оптимальных стратегий он будет пропускать даже больше мячей при всех других своих вариантах поведения, если только форвард будет применять свою оптимальную смешанную стратегию 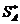(а он обязательно будет её применять, если его тренер знаком с теорией игр!!). В заключение данного раздела автор хочет отметить, что не знает наверняка, но уверен в том, что тренеры профессиональных футбольных клубов используют на практике даже гораздо более сложные математические модели для организации подготовки к матчам.

Раздел 13