Функциональные математические модели
Математическую модель М объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования этого объекта и образующих в общем случае следующие подмножества [27] (рис.1.6): совокупность входных воздействий на систему 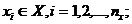 совокупность воздействий внешней среды
совокупность воздействий внешней среды 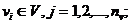 совокупность внутренних (собственных) параметров системы
совокупность внутренних (собственных) параметров системы 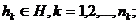 совокупность выходных характеристик системы
совокупность выходных характеристик системы 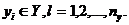
При этом входные воздействия, воздействия внешней среды и внутренние параметры системы являются независимыми переменными, а выходные характеристики системы - зависимыми переменными. Среди этих переменных могут быть управляемые и неуправляемые. Последние не зависят от желания расчетчика, работающего с моделью. Иногда управляемые величины называют параметрами.
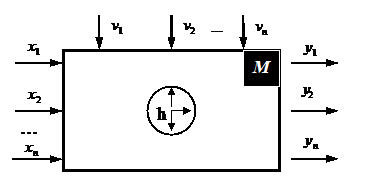
Рис. 1.6. Схема математической модели
Рассмотрим математическую модель для расчета пролетного строения моста. Постоянная, временная и другие нагрузки являются входными воздействиями. Выходными переменными являются показатели напряженно-деформированного состояния, управлять которыми расчетчик может путем изменения внутренних параметров системы. Последние могут быть представлены геометрическими характеристиками конструкций и физическими свойствами материала, из которого они изготовлены. Причем конструктивную схему пролетного строения и размеры его элементов обычно назначают предварительно и в этом смысле они являются неуправляемыми параметрами, а размеры поперечных сечений — типичный представитель управляемых параметров. К воздействиям внешней среды здесь относятся возможные осадки опор и температурные воздействия, которые вызывают появление дополнительных напряжений и тем самым влияют на выходные переменные.
Математическое описание поведения объекта моделирования во времени t можно представить в следующем виде:
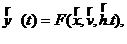 (1.8)
(1.8)
а для статических моделей - в форме равенства
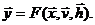 (1.9)
(1.9)
Эти зависимости называются законами функционирования системы: они могут быть заданы в виде функции, функционала, логических условий, или в алгоритмической либо табличной формах. Операторы F, f преобразуют независимые переменные в зависимые. Реализация этих преобразований выполняется с помощью алгоритма функционирования А. Один и тот же закон функционирования F системы S может быть обеспечен различными способами, т. е. с помощью множества различных алгоритмов функционирования А. Совокупность зависимостей выходных характеристик при законе функционирования типа (1.9) называется выходной траекторией. Если фиксировать отдельные моменты времени, то состояния системы S в эти моменты времени могут быть интерпретированы как координаты точки в фазовом пространстве. Причем каждой реализации процесса будет соответствовать некоторая фазовая траектория, а совокупность всех возможных значений состояний называется пространством состояний объекта моделирования.
Подготовка данных и обработка результатов
Моделирования систем
Исходные данные для моделирования и его результаты часто представляют собой массивы случайных чисел. Это относится как к составляющим вектора внешних сил (постоянная нагрузка, временная нагрузка и др.), так и к выходным данным, например к результатам многократных повторений вычислительного эксперимента (прогонов модели). Такие массивы должны быть упорядочены с целью получения данных, удобных для моделирования или разработки практических рекомендаций по результатам моделирования. Обработку массивов случайных чисел производят по правилам математической статистики.
Остановимся на тех правилах, которые представляют непосредственный интерес для решения следующих задач:
• как подобрать подходящий теоретический закон распределения случайных чисел с тем, чтобы использовать его для генерации случайных чисел при моделировании систем или для прогнозирования наибольших (наименьших) возможных значений этих чисел;
• как правильно прогнозировать наибольшие или наименьшие значения случайных чисел;
• как исключить ошибки получения экспериментальных данных и как отсеивать ложные результаты;
• как найти минимальное, но необходимое число опытов, в том числе прогонов модели, для получения достоверных результатов;
• можно ли объединять две группы случайных величин в одну общую группу.
