Расчет коэффициентов уравнения множественной линейной регрессии.

Истинные значения коэффициентов bj по выборке получить невозможно. Вместо теоретического уравнения оценивается эмпирическое уравнение регрессии для индивидуальных наблюдений: 𝑦𝑖 = 𝑏0 +𝑏1𝑥𝑖1 +𝑏2𝑥𝑖2 +⋯+𝑏𝑚𝑥𝑖𝑚 +𝑒𝑖. (5.5) Здесь 𝑏0, 𝑏1, 𝑏2,…,𝑏𝑚- эмпирические коэффициенты регрессии (оценки теоретических коэффициентов (𝛽0,𝛽1,𝛽2,…,𝛽𝑚). 𝑒𝑖- остатки (оценки отклонений 𝜀𝑖). Согласно МНК, для нахождения оценок 𝑏0; 𝑏1;…;𝑏𝑚 минимизируется сумма квадратов остатков: 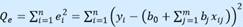Данная функция является квадратичной относительно неизвестных коэффициентов. Она ограничена снизу, следовательно, имеет минимум. 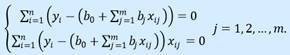Необходимым условием минимума Qe является равенство нулю частных производных Приравнивая их к нулю, получаем систему m + 1 линейных уравнений с m + 1 неизвестными: Эта система называется системой нормальных уравнений. Данные реальных статистических наблюдений всегда приводят к единственному решению этой системы. В случае множественной линейной регрессии удобнее искать коэффициенты уравнения регрессии, используя матричный метод решения. (В случае парной линейной регрессии, также можно было использовать матричный метод решения.) Представим данные наблюдений и соответствующие коэффициенты в матричной форме: Х – матрица объясняющих переменных размера n × (m+1), в которой xij – значение переменной Xj в i-м наблюдении; 1 (единица в первом столбце) соответствует переменной при b0. 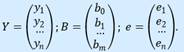Здесь Y – матрица размера n × 1 наблюдаемых значений зависимой переменной Y; B - матрица размера (m+1) × 1 оценок коэффициентов модели; е – матрица остатков размера n × 1 (отклонений наблюдаемых значений 𝑦𝑖 от расчетных значений 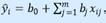, получаемых по линии регрессии). Уравнение регрессии в матричной форме: 𝑌 = 𝑋𝐵 +𝑒. (5.11) 𝑒 = 𝑌 −𝑋𝐵. (5.12) Функция, которая минимизируется 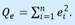Общая формула вычисления вектора B оценок коэффициентов модели множественной линейной регрессии: 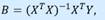(5.14) здесь XT – транспонированная матрица 𝑋, 𝑋𝑇 ∙𝑋 - произведение матриц, (𝑋𝑇 ∙𝑋)в степени−1 матрица обратная к матрице 𝑋𝑇 ∙𝑋. Вывод: Полученные общие соотношения (5.14) справедливы для уравнений регрессии с произвольным количеством m объясняющих переменных.

12. Множественная линейная регрессия. Дисперсия и стандартные ошибки коэффициентов. Коэффициенты R2 и R2

Для такой проверки используется коэффициент детерминации R 2 , который в общем случае рассчитывается по формуле: 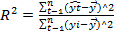. Величина R² является мерой объясняющего качества уравнения регрессии по сравнению с горизонтальной линией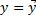

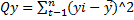- полная сумма квадратов отклонений – мера разброса (рассеивания) наблюдаемых значений объясняемой переменной y относительно ее среднего значения 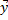. 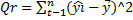- объясненная сумма квадратов отклонений – мера разброса, объясненного уравнением регрессии. 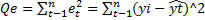- остаточная (необъясненная) сумма квадратов отклонений – мера разброса точек вокруг линии регрессии.

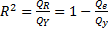Справедливо соотношение: 0 ≤ 𝑅^2 ≤ 1. Чем ближе R^2 к 1, тем больше уравнение регрессии объясняет поведение Y. В отличии от случая парной регрессии, для множественной регрессии R^2 является неубывающей функцией числа объясняющих переменных. Каждая следующая добавленная объясняющая переменная может лишь дополнить информацию, объясняющую поведение Y, и увеличить R^2 .

Для множественной регрессии используется скорректированный (исправленный) коэффициент детерминации для получения несмещенных оценок: 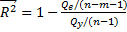где: 𝑄𝑦 /(𝑛 − 1) - несмещенная оценка общей дисперсии. Число ее степеней свободы равно (n – 1). (Одна степень свободы теряется при вычислении 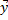); 𝑄𝑒 /(𝑛 − 𝑚 − 1) - несмещенная оценка остаточной дисперсии. Ее число степеней свободы равно (n – m – 1). Потеря (m+1) степени свободы связана с необходимостью решения системы (m+1) линейного уравнения при определении коэффициентов эмпирического уравнения регрессии.

Скорректированный (исправленный) коэффициент детерминации 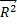можно представить в виде:

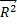= 1 − (1 − 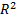) ∙ 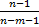. Видно, что 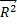< 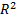для m > 1. С увеличением числа объясняющих переменных m скорректированный коэффициент детерминации 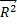растет медленнее, чем 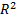; он корректируется в сторону уменьшения с ростом числа объясняющих переменных.

Отметим: 1). 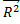= 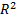только при 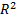= 1 (функциональная зависимость). При полном отсутствии корреляции ( 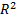= 0) скорректированный коэффициент детерминации может принимать отрицательные значения. 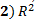увеличивается при добавлении новой объясняющей переменной только тогда, когда t - статистика для этой переменной по модулю больше единицы. Поэтому новые переменные можно добавлять в модель до тех пор, пока растет 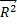. 3). 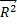рассматривается лишь как один из ряда показателей, который нужно анализировать, чтобы уточнить построенную модель регрессии. (Существуют случаи, когда неправильная спецификация модели приводит к высокому значению .)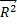