Расчет коэффициентов уравнения множественной линейной регрессии. Система нормальных уравнений

Истинные значения коэффициентов bj по выборке получить невозможно. Вместо теоретического уравнения оценивается эмпирическое уравнение регрессии для индивидуальных наблюдений: 𝑦𝑖 = 𝑏0 + 𝑏1 𝑥𝑖1 + 𝑏2 𝑥𝑖2 + ⋯ + 𝑏𝑚 𝑥𝑖𝑚 + 𝑒𝑖 . (5.5) Здесь 𝑏0 , 𝑏1 , 𝑏2 , … , 𝑏𝑚 - эмпирические коэффициенты регрессии (оценки теоретических коэффициентов (𝛽0 , 𝛽1 , 𝛽2 , … , 𝛽𝑚 ). 𝑒𝑖 - остатки (оценки отклонений 𝜀𝑖 ). Согласно МНК, для нахождения оценок 𝑏0 ; 𝑏1 ; … ; 𝑏𝑚 минимизируется сумма квадратов остатков: 𝑄𝑒 = 𝑒𝑖 𝑛 2 𝑖=1 = 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 2 𝑛 𝑖=1 . (5.6) Данная функция является квадратичной относительно неизвестных коэффициентов. Она ограничена снизу, следовательно, имеет минимум. Необходимым условием минимума Qe является равенство нулю частных производных 𝜕𝑄𝑒 𝜕𝑏𝑗 = 0, 𝑗 = 0, 1, 2, … , 𝑚. (5.7) Приравнивая их к нулю, получаем систему m + 1 линейных уравнений с m + 1 неизвестными: 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 𝑛 𝑖=1 = 0 𝑦𝑖 − 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 𝑥𝑖𝑗 𝑛 𝑖=1 = 0 𝑗 = 1, 2, … , 𝑚. (5.8) Эта система называется системой нормальных уравнений. Представим данные наблюдений и соответствующие коэффициенты в матричной форме: 𝑋 = 1 𝑥11 𝑥12 1 𝑥21 𝑥22 1 𝑥31 𝑥32 ⋯ ⋯ ⋯ 𝑥1𝑚 𝑥2𝑚 𝑥3𝑚 ⋯ ⋯ ⋯ ⋯ ⋯ 1 𝑥𝑛1 𝑥𝑛2 ⋯ 𝑥𝑛𝑚 . (5.9) Х – матрица объясняющих переменных размера n × (m+1), в которой xij – значение переменной Xj в i-м наблюдении; 1 соответствует переменной при b0. 𝑌 = 𝑦1 𝑦2 … 𝑦𝑛 ; 𝐵 = 𝑏0 𝑏1 … 𝑏𝑚 ; 𝑒 = 𝑒1 𝑒2 … 𝑒𝑛 . (5.10) Здесь Y – матрица размера n × 1 наблюдаемых значений зависимой переменной Y; B - матрица размера (m+1) × 1 оценок коэффициентов модели; е – матрица остатков размера n × 1 (отклонений наблюдаемых значений 𝑦𝑖 от расчетных значений 𝑦 𝑖 = 𝑏0 + 𝑏𝑗 𝑥𝑖𝑗 𝑚 𝑗=1 , получаемых по линии регрессии). Уравнение регрессии в матричной форме: 𝑌 = 𝑋𝐵 + 𝑒. (5.11) 𝑒 = 𝑌 − 𝑋𝐵. (5.12) Функция, которая минимизируется 𝑄𝑒 = 𝑒𝑖 𝑛 2 𝑖=1 . (5.13). Общая формула вычисления вектора B оценок коэффициентов модели множественной линейной регрессии: 𝐵 = (𝑋 𝑇 𝑋) −1 𝑋 𝑇 𝑌, (5.14) здесь X T – транспонированная матрица 𝑋, 𝑋 𝑇 ∙ 𝑋 - произведение матриц, (𝑋 𝑇 ∙ 𝑋) −1 матрица обратная к матрице 𝑋 𝑇 ∙ 𝑋. Вывод: Полученные общие соотношения (5.14) справедливы для уравнений регрессии с произвольным количеством m объясняющих переменных.

83. Множественная линейная регрессия. Коэффициенты R2 и Ṝ2

Обычно на любой экономический показатель влияет не один, а несколько факторов. В этом случае вместо функции парной регрессии 𝑀(𝑌|𝑋 = 𝑥) = 𝑓(𝑥) рассматривается функция множественной регрессии: 𝑀(𝑌|𝑋1 = 𝑥1 ; 𝑋2 = 𝑥2 ; … ; 𝑋𝑚 = 𝑥𝑚 ) = 𝑓(𝑥1 ; 𝑥2 ; … ; 𝑥𝑚 ).

Теоретическая модель множественной линейной регрессии имеет вид: 𝑌 = 𝛽0 + 𝛽1𝑋1 + 𝛽2𝑋2 + ⋯ + 𝛽𝑚 𝑋𝑚 + 𝜀 (5.2) или для индивидуальных наблюдений: 𝑦𝑖 = 𝛽0 + 𝛽1 𝑥𝑖1 + 𝛽2 𝑥𝑖2 + ⋯ + 𝛽𝑚 𝑥𝑖𝑚 + 𝜀, (5.3) 𝑖 = 1, 2, … 𝑁, где N – объем генеральной совокупности. (ИЛИ 𝑦𝑖 = 𝑏0 + 𝑏1 𝑥𝑖1 + 𝑏2 𝑥𝑖2 + ⋯ + 𝑏𝑚 𝑥𝑖𝑚)

Для проверки качества уравнения регрессии в целом используется коэффициент детерминации R^2 , который в общем случае рассчитывается по формуле:

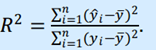
Величина R^2 является мерой объясняющего качества уравнения регрессии по сравнению с горизонтальной линией y= .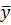

Справедливо соотношение 0<=R2<=1. Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение Y.
Длямножественной регрессии коэффициент детерминации является неубывающей функциейчисла объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R², так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной.
Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится так называемый скорректированный (исправленный) коэффициент детерминации:

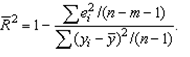
Соотношение может быть представлено в следующем виде: