Парная линейная регрессия. Взаимосвязи эконом переменных

Парная линейная регрессия. Взаимосвязи эконом переменных

В модели парной линейной регрессии одна из величин Х выделяется как независимая (объясняющая), а другая Y как зависимая (объясняемая). Например, рост дохода ведет к увеличению потребления; рост цены ведет к снижению спроса; снижение процентной ставки ведет к увеличению инвестиций. Независимая переменная Х называется также входной, экзогенной, предикторной (предсказывающей), фактором, регрессом, факторной переменной. Зависимая переменная Y называется также выходной, результирующей, эндогенной, результативным признаком, функцией отклика. Определение: Зависимость среднего значения переменной Y, т.е. условного математического ожидания Y при данном значении Х = х M 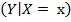= 𝑓(𝑥), называется функцией парной регрессии Y на Х. Реальные значения Y могут быть различными при одном и том же значении Х = х, поэтому фактическая зависимость имеет вид: Y = M(Y│x) +ε, (2.2) где величина ε называется случайным отклонением. Уравнение (2.2) называется парным регрессионным уравнением (моделью). Причины присутствия ε в регрессионных уравнениях Отметим причины присутствия случайного члена в регрессионных уравнениях: 1) Включение в модель не всех объясняющих переменных. Например, спрос на товар определяется не только его ценой, но и ценами на товары – заменители, доходом потребителей, их вкусами и т.д. 2) Неправильный выбор вида модели (ошибка спецификации). 3) Ошибки измерений. 4) Ограниченность статистических данных. 5) Непредсказуемость человеческого фактора.

Суть регрессионного анализа.

Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.

Задачи регрессионного анализа состоят в том, чтобы по результатам наблюдений, то есть по выборке ограниченного объема (x_i;y_i), i = 1;2;…; n: 1) Получить наилучшие точечные и интервальные оценки параметров 𝛽₀ и 𝛽₁. 2) Проверить статистические гипотезы о параметрах модели. 3) Проверить адекватность модели результатам наблюдений.

Множественная линейная регрессия. Определение параметров уравнения регрессии.

Функция множественной регрессии: 𝑀(𝑌|𝑋1 = 𝑥1; 𝑋2 = 𝑥2;…;𝑋𝑚 = 𝑥𝑚) = 𝑓(𝑥1;𝑥2;…;𝑥𝑚). (5.1) Теоретическая модель множественной линейной регрессии имеет вид: 𝑌 = 𝛽0 +𝛽1𝑋1 +𝛽2𝑋2 +⋯+𝛽𝑚𝑋𝑚 +𝜀 (5.2) или для индивидуальных наблюдений: 𝑦𝑖 = 𝛽0 +𝛽1𝑥𝑖1 +𝛽2𝑥𝑖2 +⋯+𝛽𝑚𝑥𝑖𝑚 +𝜀, (5.3) 𝑖 = 1,2,…𝑁, где N – объем генеральной совокупности. После выбора в качестве модели линейной функции множественной регрессии необходимо оценить коэффициенты регрессии. Пусть имеется n наблюдений вектора объясняющих переменных 𝑋 = (𝑋1; 𝑋2;..𝑋𝑚) и зависимой переменной Y: (𝑥𝑖1; 𝑥𝑖2; …;𝑥𝑖𝑚;𝑦𝑖), 𝑖 = 1,2,…,𝑛. (5.4) Если 𝑛 = 𝑚 +1, то оценки коэффициентов рассчитываются единственным образом. Здесь 𝑚 – число объясняющих переменных. Если 𝑛 < 𝑚 +1, то система будет иметь бесконечное множество решений. Если 𝑛 > 𝑚 +1, то нельзя подобрать линейную функцию (5.2), точно удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, т.е. нахождения оценок параметров модели (5.3), при которых линейная функция дает наилучшее приближение для имеющихся наблюдений.

Нелинейная регрессия. Виды моделей. Примеры.

1) Логарифмические (лог-линейные) модели. Предположим, экономическая зависимость моделируется формулой Y=A 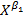, где А и 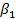- параметры модели (т.е. константы, подлежащие определению). Фунция Y=A 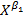может отражать зависимость спроса 𝑌 на изучаемое благо от его цены X (𝛽₁ < 0) или от дохода X (𝛽₁ > 0). При такой интерпретации переменных X и 𝑌 функция Y=A 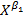называется функцией Энгеля.

2) Полулогарифмические модели - модели вида 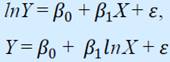(8,12)

Такие модели обычно используют в тех случаях, когда необходимо определять темп роста или прироста каких-либо экономических показателей.

-- Лог-линейная модель. Рассмотрим зависимость, хорошо известную в финансовом анализе 𝑌_𝑡=𝑌₀(1+𝑟)^𝑡 , где Y₀ — начальная величина переменной Y (например, первоначальный вклад в банке); 𝑟 — сложный темп прироста величины Y (процентная ставка и инфляция); Yt — значение величины Y в момент времени t (вклад в банке в момент времени t). Модель (8.12) легко сводится к полулогарифмической модели (8.10). Действительно, прологарифмировав имеем: lnYt = lnY₀ + tln(1 + r).

-- Линейно-логарифмическая модель .Рассмотрим так называемую линейно-логарифмическую модель Y = 𝛽0 + 𝛽₁lnX + 𝜀.Она сводится к линейной модели заменой Х*= lnХ. В данной модели коэффициент 𝛽₁ определяет изменение переменной Y вследствие единичного относительного прироста X (например, на 1%), т.е. характеризует отношение абсолютного изменения Y к относительному изменению X.

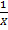3) Обратная модель - модель вида Y=𝑌=𝛽₀+𝛽₁∙ +𝜀. Эта модель сводится к линейной заменой Х*= . Данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной X асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к 𝛽₀.

4) Степенная модель. Степенная функция вида 𝑌=𝛽₀+𝛽₁𝑋+𝛽₂𝑋²+⋯+𝛽_𝑚𝑋^𝑚+𝜀 часто отражает ту или иную экономическую зависимость

5) Показательная модель Показательная функция вида 𝑌=𝛽₀𝑒^𝛽₁^𝑋 также достаточно широко применяется в эконометрическом анализе (здесь е 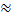2,7). Наиболее важным ее приложением является ситуация, когда анализируется изменение переменной Y с постоянным темпом прироста во времени. В этом случае переменная X символически заменяется переменной t: 𝑌=𝑏₀𝑒^𝛽₁^{𝑡 .} Данная функция путем логарифмирования (lne^𝛽₁^𝑡 = β₁t) сводится к лог-линейной модели 𝑙𝑛𝑌=𝑙𝑛𝛽₀+𝛽₁𝑡.

Суть гетероскедастичности.

Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда-Квандта и тест Глейзера.

Гетероскедастичность может иметь место и при использовании в качестве данных наблюдений временных рядов (𝑥_𝑡 , 𝑦_𝑡). Если значения 𝑥_𝑡 и 𝑦_𝑡 увеличиваются со временем, то, возможно, и дисперсия случайной составляющей также будет расти со временем. Наличие гетероскедастичности можно проследить из графика зависимости квадрата остатков 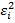от значения объясняющего признака 𝑥_𝑖. Если все отклонения находятся внутри полосы постоянной ширины, параллельной оси абсцисс, гетероскедастичность не наблюдается. Во всех остальных случаях гетероскедастичность наблюдается.

21. Последствия гетероскедастичности:

· Оценки коэффициентов по-прежнему останутся несмещёнными и линейными

· Оценки не будут эффективными (т. е, они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра), Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок

· Дисперсии оценок будут рассчитываться со смещением.

Поэтому выводы, получаемые на основе соответствующих t- и F- статистик, а также интервальные оценки коэффициентов регрессии будут ненадежными. Следовательно, статистические выводы, могут быть ошибочными и приводить к неверным заключениям по построенной модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК- оценок параметров. Следовательно, статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

22. Обнаружение гетероскедастичности в каждом конкретном случае является сложной задачей. Для знания дисперсий отклонений необходимо знать распределение случайной величины Y, соответствующее выбранному значению 𝑥_𝑖 . Практически, для каждого конкретного значения 𝑥_𝑖 определяется единственное значение 𝑦_𝑖 , что не позволяет оценить дисперсию случайной величины Y. Поэтому, не существует какого-либо однозначного метода определения гетероскедастичности.

Для определения наличия в выборке гетероскедастичностс используются тесты: графический анализ остатков, тест ранговой корреляции Спирмена, тест Глейзера и тест Голдфельда-Квандта. Выбор обусловлен относительной простотой тестов и наиболее частым их употреблением.

Тест Голдфелда Квандта. Тест выполняется в предположении, что стандартное отклонение 𝜎_𝑖 = 𝜎(𝜀)_𝑖 пропорционально значению переменной X в этом наблюдении, т.е. 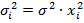, 𝑖 = 1,2, … ,𝑛. Второе предположение - 𝜀_𝑖 имеет нормальное распределение и отсутствует автокорреляция остатков. Последовательность теста Голдфелда-Квандта: 1. Все 𝑛 наблюдений удорядочиваются по величине X. 2. Вся упорядоченная выборка после этого разбивается на три группы (подвыборки) размерностей k, (𝑛 - 2k), k соответственно.3. Оцениваются отдельно регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений) 𝑆₁ = 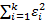будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений) 𝑆₃ = 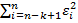. 4. Для сравнения дисперсий 𝑆₁ и 𝑆₃ строится следующая F-статистика: F= 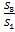∙ 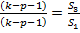, где p – число объясняющих переменных в каждом уравнении регрессии.

При сделанных предположениях относительно случайных отклонений, построенная 𝐹 -статистика имеет распределение Фишера с числами степеней свободы 𝜈₁ = 𝜈₂ = 𝑘 − 𝑝 − 1. 5. Если 𝐹набл = 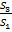> 𝐹кр = 𝐹_{𝛼;𝜈1;𝜈2} , то гипотеза об отсутствии гетероскедастичности отклоняется. Здесь 𝛼 — выбранный уровень значимости. Отметим, этот тест предназначен для анализа больших массивов данных и не всегда его результаты совпадают с результатами других тестов при недостаточном числе наблюдений.

Устранение автокорреляции

Используем авторегрессонную схему первого порядка AR(1). Вместо переменных x, y рассмотрим новые переменные x*, y*, значения которых вычисляются по правилу: 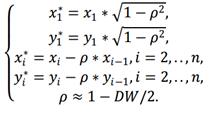Пусть 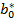=b₀(1 − 𝜌). Коэффициент 𝜌 = 1 − 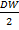= 0,4205. С помощью обычного МНК по переменным x* и y* оцениваем коэффициенты уравнения 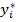= 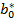+ 𝑏₁ 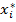. Далее находим 𝑏₀ = 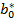/(1 − 𝜌).

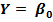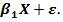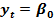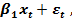
Так как автокорреляция чаще всего вызывается неправильной спецификацией модели, то необходимо, прежде всего, скорректировать саму модель. Для простоты изложения AR(1) рассмотрим модель парной линейной регрессии: + Тогда наблюдениям t и (t - 1) соответствуют формулы: + + 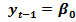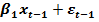Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка: 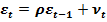, где — случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 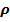известен. 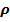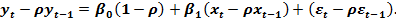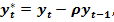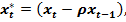Вычтем из второй формулы соотношение третьей, умноженное на : Положив 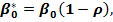получим: .

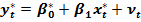Так как по предположению коэффициент 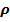известен, то очевидно, у*, x_t, v_t вычисляются достаточно просто. В силу того что случайные отклонения v_t удовлетворяют предпосылкам МНК, оценки параметров в 0 и в 1 будут обладать свойствами наилучших линейных несмещенных оценок.

Фиктивные переменные сдвига. Пример

Фиктивная переменная — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. Фиктивная переменная сдвига - это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной.

Фиктивная переменная сдвига. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых лиц уравнение регрессии имеет вид: 𝒚= 𝒃𝟎+𝒃𝟏∗𝒙+𝜺, где y - количество потребляемого кофе; x - цена. Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 𝑦1=𝑏0+𝑏11∗𝑥1+𝜀1 и женского - 𝑦2=𝑏0+𝑏12∗𝑥2+𝜀2. Различия в потреблении кофе проявятся в различии средних 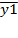и .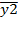

Вместе с тем сила влияния x на y может быть одинаковой, т.е. 𝑏1≈𝑏11≈𝑏12. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения у1 и у2 и, вводя фиктивные переменные, можно прийти к следующему выражению: 𝑦=𝑎1∙𝑧1+𝑎2∙𝑧2+𝑏1∙𝑥+𝜀, (8.2) где 𝑧1 и 𝑧2 - фиктивные переменные, принимающие значения:

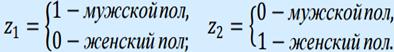
В общем уравнении регрессии зависимая переменная у рассматривается не только как функция цены 𝑥, но и пола (𝑧1;𝑧2). Переменная z рассматривается как двоичная переменная, принимающая всего два значения: 1 и 0. При этом когда 𝑧1 = 1, то 𝑧2 = 0, и наоборот. Для лиц мужского пола, когда 𝑧1 = 1 и 𝑧2 = 0, объединенное уравнение регрессии составит: у = а1 + 𝑏1∙𝑥, а для лиц женского пола, когда 𝑧1 = 0 и 𝑧2 = 1 уравнение регрессии у = а2 + 𝑏1∙𝑥. Иными словами, различия в потреблении кофе для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: 𝑎1≠𝑎2. Параметр 𝑏1 является общим для всей совокупности лиц, как для мужчин, так и для женщин.

Однако при введении двух фиктивных переменных 𝑧1 и 𝑧2 в модель у = а1∙𝑧1 + а2∙𝑧2+𝑏1∙𝑥 +𝜀 (8.4) применение МНК для оценивания параметров а1 и а2 приведет к вырожденной матрице исходных данных, и невозможности получения оценок коэффициентов уравнения регрессии. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид у = 𝑏0 + а1∙𝑧1 + а2∙𝑧2+𝑏1∙𝑥 +𝜀.

Предполагая при параметре 𝑏0 независимую переменную, равную 1, имеем следующую матрицу исходных данных (объясняющих переменных):

В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена

Выходом из создавшегося затруднения может явиться переход к уравнениям y = 𝒃𝟎+𝑏1𝑥+𝑏2𝑧1+𝜀, или y = 𝒃𝟎+𝑏1𝑥+𝑏2𝑧2+𝜀, т.е. каждое уравнение включает только одну фиктивную переменную 𝑧1 или 𝑧2.

Предположим, что определено уравнение 𝑦=𝑏0+𝑏1∙𝑥+𝑏2∙𝑧+𝜀, где z принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин будут получены из уравнения 𝑦=𝑏0+𝑏1∙𝑥+𝑏2. Для женщин соответствующие значения получим из уравнения 𝑦=𝑏0+𝑏1∙𝑥. Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: 𝑏0 - для женщин и 𝑏0+𝑏2 - для мужчин.

Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Вывод: Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели

Пример. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный. При использовании трех категорий домов вводятся две фиктивные переменные: z1 и z2. Пусть переменная z1 принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная z2 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные z1 и z2 принимают значения 0 для домов типа «хрущевки».

Предположим, что уравнение регрессии с фиктивными переменными имеет вид: у = 320 + 500x+2200z1 +1600z2. Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид: «хрущевки» - у = 320 + 500x; панельные - у = 2520 + 500x; кирпичные - у = 1920 + 500x. Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых z1 = z2 = 0

Параметр при z1, равный 2200, означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 ден.ед. выше, чем в «хрущевках». Соответственно параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600 ден.ед. при неизменной величине полезной площади по сравнению с указанным типом домов.

В зависимости от того, является уравнение системы идентифицируемым или сверхидентифицируе-мым, используются различные методы оценки его структурных параметров. Косвенный метод наименьших квадратов позволяет построить оценкипараметров только точно идентифицируемых уравнений. КМНК включает в себя этапы: 1.По структурной форме модели строится приведенная форма 2.Определяются МНК-оценки параметров приведенной формы 3.По МНК-оценкам приведенной формы вычисляются оценки параметров структурной формы4

40. Каково содержание двухшагового метода наименьших квадратов?

Если система сверхидентифицируема, то КМНК не используется, т.к. он не дает однозначных оценок для параметров структурной формы. Для нахождения коэффициентов сверхиндифицируемых уравнений применяется двухшаговый МНК (ДМНК). Двухшаговый МНК состоит в следующем: 1) Составляют приведенную форму модели и определяют значения коэффициентов для каждого ее уравнения в отдельности с помощью обычного МНК. 2) Выявляют эндогенные переменные, находящиеся в правой части структурного уравнения (коэффициенты которого определяют двухшаговым МНК) и находят их расчетные значения по полученным на первом этапе соответствующим уравнениям приведенной формы модели. 3) С помощью обычного МНК находят коэффициенты каждого структурного уравнения в отдельности, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, находящихся в правой части данного структурного уравнения, полученные на втором этапе.

Сверхидентифицируемая структурная модель может быть двух типов: 1. Все уравнения системы сверхидентифицируемы. 2. Система содержит наряду со сверхидентифицируемыми уравнениями и точно идентифицируемые уравнения. Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Для точно идентифицируемых систем ДМНК дает тот же результат, что КМНК.

Парная линейная регрессия. Взаимосвязи эконом переменных

В модели парной линейной регрессии одна из величин Х выделяется как независимая (объясняющая), а другая Y как зависимая (объясняемая). Например, рост дохода ведет к увеличению потребления; рост цены ведет к снижению спроса; снижение процентной ставки ведет к увеличению инвестиций. Независимая переменная Х называется также входной, экзогенной, предикторной (предсказывающей), фактором, регрессом, факторной переменной. Зависимая переменная Y называется также выходной, результирующей, эндогенной, результативным признаком, функцией отклика. Определение: Зависимость среднего значения переменной Y, т.е. условного математического ожидания Y при данном значении Х = х M 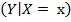= 𝑓(𝑥), называется функцией парной регрессии Y на Х. Реальные значения Y могут быть различными при одном и том же значении Х = х, поэтому фактическая зависимость имеет вид: Y = M(Y│x) +ε, (2.2) где величина ε называется случайным отклонением. Уравнение (2.2) называется парным регрессионным уравнением (моделью). Причины присутствия ε в регрессионных уравнениях Отметим причины присутствия случайного члена в регрессионных уравнениях: 1) Включение в модель не всех объясняющих переменных. Например, спрос на товар определяется не только его ценой, но и ценами на товары – заменители, доходом потребителей, их вкусами и т.д. 2) Неправильный выбор вида модели (ошибка спецификации). 3) Ошибки измерений. 4) Ограниченность статистических данных. 5) Непредсказуемость человеческого фактора.