Простейшие геометрические фигуры на плоскости.

Как сказано выше, из неопределяемых, основных понятий геометрии (точек, прямых и т.д.) образуются новые объекты, геометрические фигуры, которые вводятся уже по определению.

Опр.1. Геометрической фигурой называется любое непустое множество точек.

Например, отрезок, точка, ромб – это геометрические фигуры.

Опр. 2. Отрезком наз. фигура, состоящая из двух данных точек А и В, и всех тех точек прямой АВ, которые лежат между этими двумя точками.

Замечание: По умолчанию понятие «между» считается всем интуитивно ясным, понимается в обыденном смысле, но с точки зрения теории это понятие должно быть определено ( что будет сделано позже).

Точки А и В –это концы отрезка, остальные точки отрезка - внутренние. Если точки А и В совпадают, то отрезок считается нулевым. Если точки А и В не входят в отрезок, то отрезок называется интервалом, открытым отрезком. В начальной школе с этими понятиями не встречаются. Отрезок [AB] иногда называют расстоянием между точками А и В, такой смысл вкладывается в понятие отрезка в начальной школе.

Если на прямой выбрана произвольная точка А, то говорят, что точка А разбивает множество точек прямой на два подмножества точек так, что точка А лежит всегда между двумя точками различных множеств разбиения.

Опр.3. Лучом прямой «а»с началом в точкеОназывается фигура, состоящая из точки О и любого из тех двух множеств точек прямой «а», на которые прямая «а»разбивается точкой О

Опр.4.Отрезок АВ ([АВ])наз. направленным, если указано направление его прочтения.

Например, АВ и ВА – разные направленные отрезки, часто их обозначают .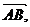

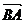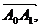
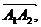
Опр. 5. Ломаной линией называется конечное множество направленных отрезков 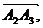… 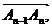заданных в определенном порядке и расположенных в пространстве так, что конец каждого отрезка, кроме последнего, совпадает с началом следующего за ним отрезка (Рис.7.)

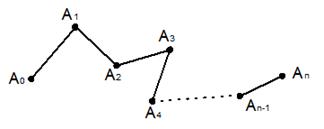
Рис.7

Замечание: Проанализируем понятие ломаной линии с точки зрения определения этого понятия.1). Задано конечное множество направленных отрезков, «множество направленных отрезков» – это родовое понятие. 2). «Направленные отрезки расположены в определенном порядке» – это первый видовой признак ломаной линии. 3). «Конец каждого отрезка, кроме последнего, совпадает с началом предыдущего отрезка» – это второй видовой признак ломаной линии. 4). «Ломаная линия» – это новое сформулированное математическое понятие.

Отрезки, составляющие ломаную, называются звеньями, общие концы двух соседних отрезков – это вершины ломаной, начало первого и конец последнего звеньев - это начало и конец ломаной, ломаная обозначается: 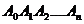. Ломаная называется плоской, если все ее звенья принадлежат одной плоскости. Ломаная называется замкнутой, если концы ломаной совпадают. Вместо термина «замкнутая ломаная», используют термин «многоугольник». С некоторыми многоугольниками знакомятся на уроках математики учащиеся начальной школы, выделим те понятия, с которыми должны ознакомиться учащиеся начальной школы в соответствии с общепринятой программой: точка, прямая, отрезок, ломаная (в конкретном виде), многоугольник (треугольник, квадрат, прямоугольник), стороны многоугольника, вершины многоугольника.

Рассмотрим на плоскости фигуру, состоящую из двух лучей ([OA);[OB)), исходящих из одной точки О. Эта фигура разбивает множество всех точек плоскости на 2 части: области 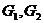. (Рис. 8)

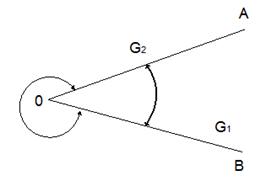
Рис.8

Опр. 6. Угломназывается фигура, состоящая из двух лучей [OA);[OB), с общим началом О и одного из тех двух множеств точек, на которые эти лучи разбивают точки плоскости.

Лучи ([OA);[OB)) – это стороны угла, точка О – вершина угла.

1)([OA);[OB)), 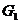-это один угол,

2)([OA);[OB)), 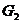-это второй угол.

В начальной школе под углом чаще понимают угол именно в таком смысле.

Если оба луча лежат на одной прямой, то возможны случаи:

1) лучи [ОА), [ОВ) – не совпадают;

2) лучи [ОА), [ОВ) – совпадают.

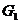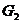Случай 1): если лучи не совпадают, то плоскость этими лучами разбивается на два множества и , ситуация соответствует принятому определению, имеем два угла: [ОА), [ОВ) и область ;

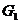[ОА), [ОВ) и область .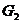

Такие углы называются развернутыми (Рис.9 ).

Опр. 7. Угол называется развернутым, если лучи ([OA);[OB)) лежат на одной прямой и не совпадают.

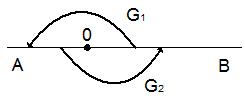
Рис.9

Случай 2): если лучи совпадают, то плоскость между двумя лучами на два множества не разбивается. Образуется только одно множество G, две точки которого можно соединить ломаной линией MNPRS (Рис.10). Для единообразия можно считать, что имеем 2 множества: 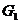- не пустое, и .

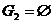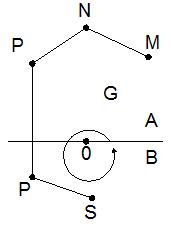
Рис.10

Опр.8. Угол называется нулевым, если его стороны совпадают.

Опр.9. Два угла называются смежными, если их объединение есть угол развернутый, а пересечение - их общая сторона.

Иначе, угол является развернутым, если: 1) 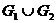, 2) 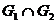- луч [ОВ) (Рис. 11)

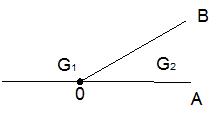
Рис. 11

.

Опр. 10. Угол называется прямым, если он равен своему смежному углу.

Наиболее часто встречающимися геометрическими фигурами на плоскости являются многоугольники и их простейшие виды. Если у многоугольника «n» сторон, то говорят об n- угольнике, если n=3. то это треугольник, если n=4, то четырехугольник и т .д. Опираясь на метод определения математического понятия через род и видовое отличие, проведем классификацию простейших геометрических фигур, с которыми могут встретиться учащиеся начальной школы при изучении математики.

Опр. 11. Треугольником называется многоугольник с тремя углами (в обычном курсе принято говорить о треугольнике как о фигуре с тремя сторонами).

Классификация треугольников, их виды, свойства сторон и углов, признаки равенства и подобия хорошо известны из курса математики основной школы.

Опр.12. Четырехугольником называется многоугольник, имеющий 4 угла.

К четырехугольникам относятся квадраты, прямоугольники, ромбы, параллелограммы, трапеции, их свойства изучаются в курсе математики основной школы.

Опр. 13. Трапецией называется четырехугольник, имеющий одну пару параллельных сторон.

Опр. 14 (1). Параллелограммом называется трапеция с параллельными боковыми сторонами.

Опр.14(2). Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

Опр.15. Ромбомназывается параллелограмм с равными смежными сторонами.

Опр. 16. Прямоугольникомназывается параллелограмм с прямым углом.

Опр. 17. Квадратомназывается ромб с прямым углом.

Опр. 18. Квадратом называется прямоугольник с равными смежными сторонами

Все приведенные определения геометрических понятий сформулированы на основе выделения родового понятия и его и видового признака.