Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Равенство нулю обеспечено, если угол между векторами -+пи\2
Векторное произведение
Векторным произведением ненулевых векторов 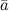 и
и 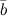 называется вектор
называется вектор 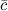 , обозначаемый символом
, обозначаемый символом 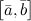 или
или 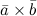 , длина которого
, длина которого 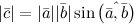
8 Смешанное произведение
Сме́шанное произведе́ние 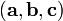 векторов
векторов 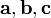 — скалярное произведение вектора
— скалярное произведение вектора 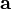 на векторное произведение векторов
на векторное произведение векторов 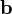 и
и 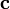 :
:
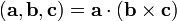 .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами 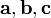 .
.
· Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
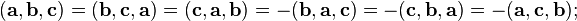
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
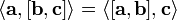
· Смешанное произведение 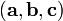 в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 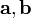 и
и 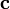 :
:
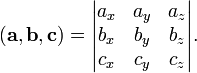
· Смешанное произведение 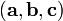 в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 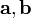 и
и 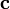 , взятому со знаком «минус»:
, взятому со знаком «минус»:
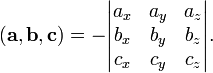
Применение:1) можно узнать компланарны ли векторы. Если abc=0, то векторы в одной плоскости.
Правая и левая тройки векторов
Определение
Три некомпланарных вектора 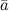 ,
, 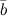 и
и 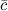 , приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
, приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов 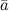 ,
, 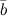 и
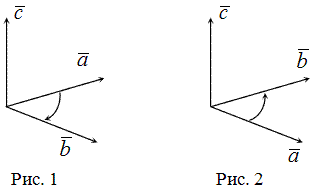
и 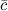 называется левой, если поворот от вектора
называется левой, если поворот от вектора 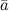 к вектору
к вектору 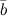 , видимый с конца третьего вектора
, видимый с конца третьего вектора 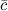 , осуществляется по ходу часовой стрелки (рис. 1).
, осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов 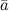 ,
, 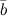 и
и 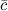 называется правой, если поворот от вектора
называется правой, если поворот от вектора 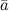 к вектору
к вектору 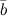 , видимый с конца третьего вектора
, видимый с конца третьего вектора 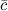 , осуществляется против хода часовой стрелки (рис. 2).
, осуществляется против хода часовой стрелки (рис. 2).
3) Смешанным произведением трех векторов 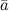 ,
, 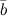 ,
, 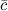 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 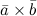 на вектор
на вектор 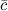 :
: 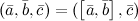
Уравнение прямой с угловым коэффициентом
Пусть заданы:
а) точка 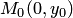 на оси ординат;
на оси ординат;
б) угол 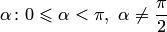 (рис.3.21,а).
(рис.3.21,а).
Требуется составить уравнение прямой, пересекающей ось ординат в заданной точке и образующей с положительным направлением оси абсцисс угол заданной величины 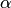 .
.
Величину, равную тангенсу угла 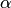 , который образует прямая с положительным направлением оси абсцисс, называют угловым коэффициентом прямой и обозначают
, который образует прямая с положительным направлением оси абсцисс, называют угловым коэффициентом прямой и обозначают 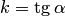 (рис.3.21,а).
(рис.3.21,а).
Выберем на прямой произвольную точку 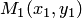 , отличную от
, отличную от 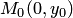 , т.е.
, т.е. 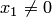 . Запишем уравнение (3.16) при
. Запишем уравнение (3.16) при 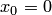 :
:
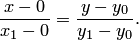
Отсюда
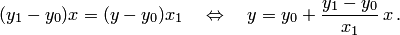
Подставляя 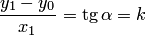 , получаем уравнение
, получаем уравнение
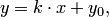
| (3.18) |
которое называется уравнением прямой с угловым коэффициентом (или уравнением прямой, разрешенным относительно 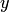 ).
). 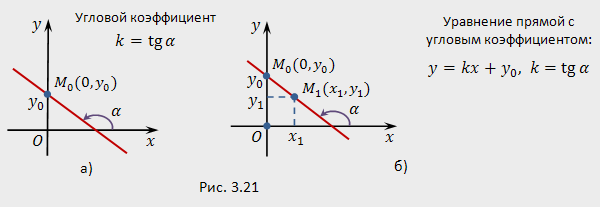
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
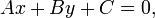
где  и
и 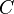 — произвольные постоянные, причем постоянные
— произвольные постоянные, причем постоянные 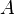 и
и 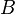 не равны нулю одновременно.
не равны нулю одновременно.
При 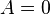 прямая параллельна оси
прямая параллельна оси 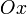 , при
, при 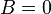 — параллельна оси
— параллельна оси 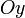 .
.
Вектор с координатами 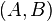 называется нормальным вектором, он перпендикулярен прямой.
называется нормальным вектором, он перпендикулярен прямой.
При 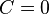 прямая проходит через начало координат.
прямая проходит через начало координат.
Также уравнение можно переписать в виде
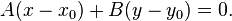
Пусть 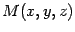 -- некоторая точка плоскости
-- некоторая точка плоскости 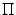 (рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.
(рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.

Вектор 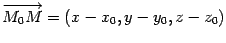 лежит на плоскости
лежит на плоскости 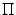 . Следовательно, вектор
. Следовательно, вектор 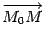 ортогонален вектору n. Если же взять точку
ортогонален вектору n. Если же взять точку 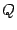 , не лежащую на плоскости
, не лежащую на плоскости 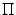 , то вектор
, то вектор 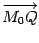 не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения (свойство 8, теорема 10.2), то условием того, что точка
не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения (свойство 8, теорема 10.2), то условием того, что точка 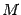 лежит в плоскости
лежит в плоскости 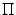 , является выполнение равенства
, является выполнение равенства
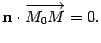 | (11.2) |
Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле (10.1), получим формулу (11.1).
Пусть r -- радиус-вектор текущей точки 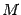 плоскости
плоскости 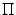 ,
, 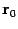 -- радиус-вектор точки
-- радиус-вектор точки 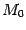 . Тогда уравнение (11.2) можно переписать в виде
. Тогда уравнение (11.2) можно переписать в виде
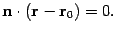
Такое уравнение обычно называют векторным уравнением плоскости 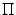 .
.
Раскроем скобки в уравнении (11.1). Так как точка 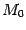 -- фиксированная, то выражение
-- фиксированная, то выражение 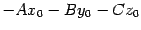 является числом, которое обозначим буквой
является числом, которое обозначим буквой 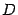 . Тогда уравнение (11.1) принимает вид
. Тогда уравнение (11.1) принимает вид
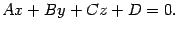 | (11.3) |
Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов 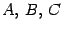 отличен от нуля, так как
отличен от нуля, так как 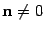 .
.
| Взаимное расположение двух плоскостей (формулировки и примеры) |
Взаимное расположение двух плоскостей характеризуется двумя возможностями. 1). Две плоскости не имеют общих точек, и , в таком случае, они называются параллельными (на рис. 28 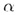 ||). ||). 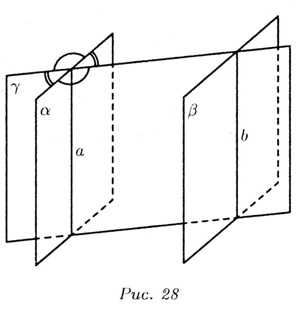 Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат обе общие точки этих плоскостей (аксиома). Таким образом, две плоскости пересекаются по прямой (на рис. 28 Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат обе общие точки этих плоскостей (аксиома). Таким образом, две плоскости пересекаются по прямой (на рис. 28 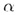 и и 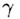 пересекаются по прямой a, a и пересекаются по прямой a, a и 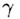 - по прямой b). Пересекающиеся плоскости образуют четыре двугранных угла. Если один из них прямой, тогда и остальные углы тоже прямые, а плоскости называются перпендикулярными. В качестве параллельных плоскостей на каждом шагу встречаем параллельные грани одного дома. Плоскости стен домов перпендикулярны плоскости земли. - по прямой b). Пересекающиеся плоскости образуют четыре двугранных угла. Если один из них прямой, тогда и остальные углы тоже прямые, а плоскости называются перпендикулярными. В качестве параллельных плоскостей на каждом шагу встречаем параллельные грани одного дома. Плоскости стен домов перпендикулярны плоскости земли. |
